
колды экз
.pdf1.Предмет коллоидной химии. Признаки объектов коллоидной химии. Поверхностная энергия и поверхностные явления. Количественные характеристики дисперсности. Классификация дисперсных систем. Коллоидная
химия и химическая технология. |
4 |
2.Поверхностное натяжение: термодинамическое определение, физический смысл, влияние природы взаимодействующих фаз. Вывод уравнения для полной (внутренней) энергии поверхностного слоя (уравнение ГиббсаГельмгольца). Зависимость
термодинамических параметров поверхности от температуры. |
5 |
3.Метод избытков Гиббса. Вывод фундаментального адсорбционного уравнения Гиббса. Гиббсовская адсорбция. Частное выражение уравнения Гиббса. Поверхностная
активность, поверхностно-активные и поверхностно-инактивные вещества. |
6 |
4.Адгезия и смачивание, определения. Уравнение Дюпре для работы адгезии. Угол смачивания и уравнение Юнга. Уравнение Дюпре-Юнга для работы адгезии. Влияние
ПАВ на адгезию и смачивание. |
9 |
5.Правило фаз Гиббса и дисперсность. Влияние кривизны поверхности (дисперсности) на внутреннее давление тел (вывод и анализ уравнения Лапласа). Капиллярные явления
(уравнение Жюрена). |
10 |
6.Влияние дисперсности на термодинамическую реакционную способность. Вывод уравнения капиллярной конденсации Кельвина. Влияние дисперсности на растворимость, константу равновесия химической реакции и температуру фазового
перехода. |
13 |
7.Методы получения дисперсных систем: диспергирование и конденсация. Уравнение Ребиндера для работы диспергирования. Адсорбционное понижение прочности (эффект Ребиндера). Конденсация физическая и химическая. Энергия Гиббса образования зародыша новой фазы при гомогенной конденсации; роль пересыщения. 14
8.Классификация механизмов адсорбции. Природа адсорбционных сил и их особенности при физической адсорбции. Вывод уравнения для энергии дисперсионного взаимодействия атома адсорбата с адсорбентом. Изотерма, изостера, изопикна
адсорбции. |
15 |
9.Мономолекулярная адсорбция, форма изотермы адсорбции. Уравнение Генри.
Основные положения теории Ленгмюра. |
16 |
10.Теopия полимолекулярной адсорбции БЭТ: исходные положения, вывод уравнения изотермы и его анализ. Линейная форма уравнения БЭТ. Определение удельной
поверхности адсорбентов, катализаторов и других пористых тел. |
17 |
10.Количественные характеристики пористых материалов: пористость, удельная поверхность, размер пор. Пористые тела корпускулярной, кристаллической и губчатой структуры, методы их получения. Классификации пор по Дубинину и теория
адсорбции. |
19 |
11.Адсорбция на пористых адсорбентах. Теория капиллярной конденсации. Капиллярноконденсационный гистерезис. Расчет и назначение интегральной и дифференциальной
кривых распределения объема пор по размерам. |
20 |
13.Потенциальная теория адсорбции Поляни. Адсорбционный потенциал. Характеристическая кривая адсорбции. Температурная инвариантность и афинность
характеристических кривых. |
22 |
14.Особенности адсорбции на микропористых адсорбентах. Обобщенное уравнение теории Дубинина (теория объемного заполнения микропор), частные случаи этого уравнения (уравнение Дубинина-Радушкевича). Расчет общего объема микропор по
изотерме адсорбции. |
23 |
15.+16 особенности адсорбции ПАВ на границе раздела раствор-воздух. Влияние строения молекул ПАВ на поверхностную активность(правило Дюкле-Траубе). Зависимость поверхностно натяжения растворов от концентраций ПАВ при соблюдении закона Генри и уравнения Ленгмюра (вывод уравнений). Поверхностное давление адсорбционной пленки ПАВ. Уравнение состояния двумерного газа для адсорбционной пленки(вывод);различные агрегатные состояния адсорбционных
пленок. Весы Ленмюра и определение размеров молекул ПАВ. |
24 |
17.Ионообменная адсорбция. Природные и синтетические иониты. Классификация ионитов по кислотно-основным свойствам. Полная и динамическая обменные емкости. Константа
растворения ионного обмена, уравнение Никольского. |
28 |
18.Вывод уравнения для скорости осаждения частиц в гравитационном поле. Условия соблюдения Стокса. Седиментационный анализ, расчет и назначение кривых
распределения по размерам. |
31 |
19.Природа броуновского движения, понятие и определение среднеквадратичного сдвига по выбранному ?. Взаимосвязь между среднеквалратичным сдвигом и коэффициентом диффузии (вывод закона Эйнштейна-Смолуховского). Экспериментальная проверка
закона. |
33 |
20.Седиментационно-диффузное равновесие. Вывод уравнения(гипсометрический закон Лапласа). Мера седиментационной устойчивости. Факторы, влияющие на
седиментационную устойчивость дисперсных систем. |
35 |
21.Механизмы образования двойного электрического слоя. Соотношения между электрическим потенциалом и поверхностным натяжением (вывод уравнений Липмана).
Элеткокапилярные кривые и определение параметров ДЭС. |
36 |
22.Общие представления о теории строения ДЭС. Уравнение Пуассона-Больцмана для диффузной части ДЭС и его решение для случая слабозаряженных поверхностей.
Уравнение Гуи-Чемпена. |
37 |
23.Современная теория строения ДЭС (теория Штерна) роль специфической адсорбции, перезарядка поверхности. Примеры образования ДЭС. Строение мицеллы (формулы
ДЭС). |
40 |
24.Электрокинетические явления. Электрокинетический потенциал. Уравнение Смолуховского для электроосмоса и электрофореза. Эффекты, не учитываемые уравнением уравнением Смолуховского (поверхностная проводимость,
электрофоретическое торможение, релаксационный эффект). |
42 |
25.Два вида устойчивых дисперсных систем. Лиофильные и лиофобные системы. Критерий лиофильности по Ребиндеру-Щукину. Факторы агрегативной устойчивости дисперсных
систем. Пример лиофольных и лиофобных дисперсных систем. |
43 |
26.Лиофильные дисперсные системы. Классификация и общая характеристика ПАВ. Термодинамика и механизм мицеллобразования. Строение мицелл ПАВ в водных и
углеводородных средах. Солюбизация. + |
45 |
27.Лиофильные дисперсные системы. Истинно растворимые и коллоидные ПАВ, их классификация. Мицеллообразование, строение мицелл; методы определения ККМ.
Факторы, влияющие на ККМ ионных и неионных ПАВ. |
45 |
28.Лиофобные дисперсные системы. Факторы агреативной устойчивости лиофобных систем. Быстрая и медленная коагуляция. Кинетика коагуляций по Смолуховскому (вывод уравнения). Определение константы скорости и времени половинной коагуляции.
Зависимость числа частиц разного порядка от времени. |
47 |
29.Теория ДЛФО. Расклинивающие давление и его составляющие. Вывод уравнения для энергии электростатического отталкивания при взаимодействии слабозаряженных поверхностей. Потенциальные кривые взаимодействия частиц для агрегативно
устойчивой и неустойчивой дисперсных систем. |
49 |
30.Природа сил притяжения и отталкивания между частицами в дисперсных системах. Вывод уравнения для энергии притяжения между частицами( теория ДЛФО). Константа Гамакера и ее физический смысл. Анализ зависимости суммарной энергии
взаимодействия частиц от расстояния между ними. |
51 |
31.Факторы агреативной устойчивости лиофобных дисперсных систем. Электролитная коагуляция (концентрационная и нейтрализационная коагуляция). Правило ШульцеГарди и закон Дерягина. Способы стабилизаци лиофобных дисперсных систем. 52
32.Структурообразование в соответсвии с теорией ДЛФО. Коагуляционно-тиксотропные и конденсационно-кристализационные структуры. Условия перехода одних структур в другие. Классификация дисперсных систем по релогическим (структурно-механическим)
свойствам. |
53 |
33.Ньютоновские жидкости, уравнение Ньютона и Пуазейля. Методы измерения вязкости. Уравнения Эйнштейна, для вязкости дисперсных систем, условия его применимости. 55
34.Реологический метод исследования структур в дисперсных системах. Реологические модели идеальных тел (модели Гука, Ньютона, Сен-Венана-Кулона). Кривые течения
реальных жидкообразных и твердообразных структурированных систем. |
56 |
35.Моделирование реологических свойств тел, модель и уравнение Бингама. Кривые течения и вязкости жидкообразной и твердообразной систем с коагуляционной
структурой. Ползучесть, предел текучести. |
57 |
1.Предмет коллоидной химии. Признаки объектов коллоидной химии. Поверхностная энергия и поверхностные явления. Количественные характеристики дисперсности. Классификация дисперсных систем. Коллоидная химия и химическая технология.
Колло́идная хи́мия (др.-греч. κόλλα — клей) — наука о дисперсных системах и поверхностных явлениях, возникающих на границе раздела фаз. Изучает адгезию, адсорбцию, смачивание, коагуляцию, электро-поверхностные явления в дисперсных системах.
Признаки коллоидных систем:
1.Гетерогенность
2.Дисперсность.
Гетерогенность количественно определяется поверхностным натяжением — величиной, характеризующей энергию единицы поверхности и являющейся фактором интенсивности. Поверхностное натяжение определяет как бы степень гетерогенности, резкость перехода от одной фазы к другой, различие между соприкасающимися фазами. Чем сильнее выражена гетерогенность и чем более резко различаются по природе сопряженные фазы, тем больше поверхностное натяжение. Отсутствие гетерогенности равнозначно отсутствию поверхностного натяжения. Гетерогенным системам присуща поверхностная энергия: G = σ·s.
Второй признак — дисперсность. Дисперсность – величина, обратная поперечному размеру частиц: D=1/а. Системы с малой дисперсностью (менее 103 см-1) не принято рассматривать как коллоидные.
Широко применяется и третья характеристика раздробленности — удельная поверхность Sуд, определяемая отношением площади межфазной поверхности к объему тела s/V, Все три характеристики раздробленности связаны между собой: с уменьшением размера а увеличиваются дисперсность D и удельная поверхность Sуд.
Классификация по кинетическим свойствам:
1.Свободнодисперсные системы (частицы не связаны друг с другом, свободное броуновское движение)
2.Связнодисперсные системы (частицы образуют пространственную решетку) Классификация по размеру частиц:
1.Ультрамикрогетерогенные системы (золи): r = 1 – 100 нм
2.Микрогетерогенные системы (суспензии): r = 100 – 104 нм
3.Грубодисперсные системы: r = 0,1 – 10 мкм
Коллоидные явления широко распространены в химической технологии. Практически нет такого химического производства, которое бы не осуществлялось с участием поверхностных явлений и дисперсных систем. Измельчение сырья и промежуточных продуктов, обогащение, в том числе флотация, сгущение, отстаивание и фильтрация, конденсация, кристаллизация и вообще процессы образования новых фаз, брикетирование, спекание, гранулирование — все эти процессы протекают в дисперсных системах, и в них большую роль играют такие коллоидно-химические явления, как смачивание, капиллярность, адсорбция, седиментация, коагуляция.
Большое распространение в химической технологии получили адсорбенты и катализаторы, которые представляют собой дисперсные системы с твердой дисперсионной средой. Адсорбция имеет самостоятельное значение для очистки и разделения веществ, извлечения ценных компонентов, хроматографии и др.
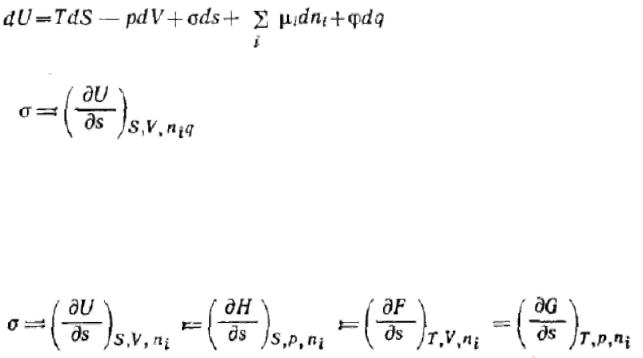
Как правило, все гетерогенные процессы в химической технологии для увеличения их скорости проводят при максимальной поверхности контакта фаз. Это значит, что системы в реакционных аппаратах находятся в состоянии суспензий, паст, пульп, эмульсий, пен, порошков, туманов, пылей. Несмотря на то что толщина поверхностных слоев не превышает несколько молекул, их роль не менее важна, чем объемных фаз, например, в процессах массопередачи (адсорбция, экстракция, сушка, испарение и др.), термоэлектронной эмиссии, смазочном действии, адгезии.
2.Поверхностное натяжение: термодинамическое определение, физический смысл, влияние природы взаимодействующих фаз. Вывод уравнения для полной (внутренней) энергии поверхностного слоя (уравнение ГиббсаГельмгольца). Зависимость термодинамических параметров поверхности от температуры.
Есть несколько определений поверхностного натяжения:
1.Поверхностное натяжение – работа образования новой поверхности в изотермическом процессе
2.Поверхностное натяжение – сила, действующая по периметру данной поверхности, отнесенная к единице длины.
3.Поверхностное натяжение – работа переноса молекул из объема тела на поверхность.
4.Термодинамическое определение поверхностного натяжения: Термодинамическое определение поверхностного натяжения вытекает из объединенного уравнения первого и второго начал термодинамики. Запишем его для гетерогенной системы относительно изменения внутренней энергии U:
]
При постоянных S, V, ni и q имеем:
]
т. е. поверхностное натяжение есть частная производная от внутренней энергии по площади поверхности раздела фаз при постоянных энтропии, объеме, числе молей компонентов и заряде.
Так как объединенное уравнение первого и второго начал термодинамики может быть записано и относительно других термодинамических потенциалов, а именно энергии Гиббса G, энергии Гельмгольца F и энтальпии Я, то при соответствующих постоянных параметрах получим:
]
Таким образом, поверхностное натяжение есть частная производная от любого термодинамического потенциала по площади межфазной поверхности при постоянных соответствующих параметрах.
Физический смысл поверхностного натяжения можно представить так: поверхностное натяжение на границе жидкости с газовой фазой – работа, расходуемая на обратимый разрыв столбика этой жидкости с поперечным сечением в 0,5 единицы площади, так как при разрыве образуется новая поверхность, равная единице площади.
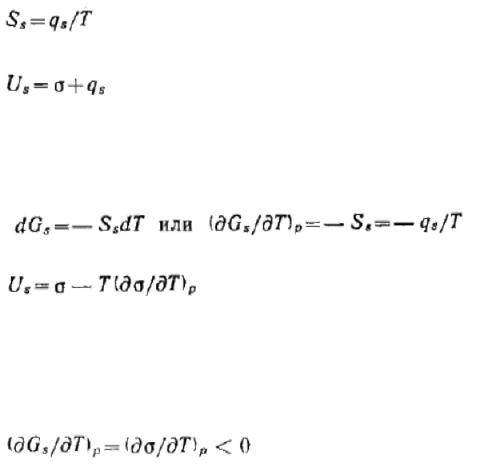
Чем сильнее межмолекулярные связи в данном теле, тем больше его поверхностное натяжение на границе с газовой фазой.
В соответствии со вторым началом термодинамики избыточная энтропия равна
]
Учитывая, что Gs = σ, получим следующее выражение:
]
Из этого уравнения следует, что внутренняя энергия поверхности складывается из энергии Гиббса и теплоты образования поверхности. Для индивидуальных веществ теплота qs всегда положительна, так как при образовании поверхности теплота поглощается. Из уравнения объединенных первого и второго начала термодинамики при постоянстве всех параметров, кроме температуры, имеем:
]
Подставлям это выражение в полученные уравнения:
]
Это уравнение называется уравнением Гиббса — Гельмгольца. Оно связывает полную поверхностную энергию с энергией Гиббса (поверхностным натяжением). Из этого уравнения следует, что для определения полной поверхностной энергии необходимо знать зависимость поверхностного натяжения от температуры. Для индивидуальных веществ теплота qs всегда положительна, а это значит, что температурный коэффициент поверхностного натяжения отрицателен:
]
Таким образом, поверхностное натяжение индивидуальных веществ на границе с газом (воздухом) снижается с повышением температуры. Для большинства неполярных жидкостей эта зависимость линейная.
3.Метод избытков Гиббса. Вывод фундаментального адсорбционного уравнения Гиббса. Гиббсовская адсорбция. Частное выражение уравнения Гиббса. Поверхностная активность, поверхностно-активные и поверхностно-инактивные вещества.
Для описания термодинамики поверхностных явлений применяют два метода: метод избыточных величин Гиббса и метод «слоя конечной толщины».
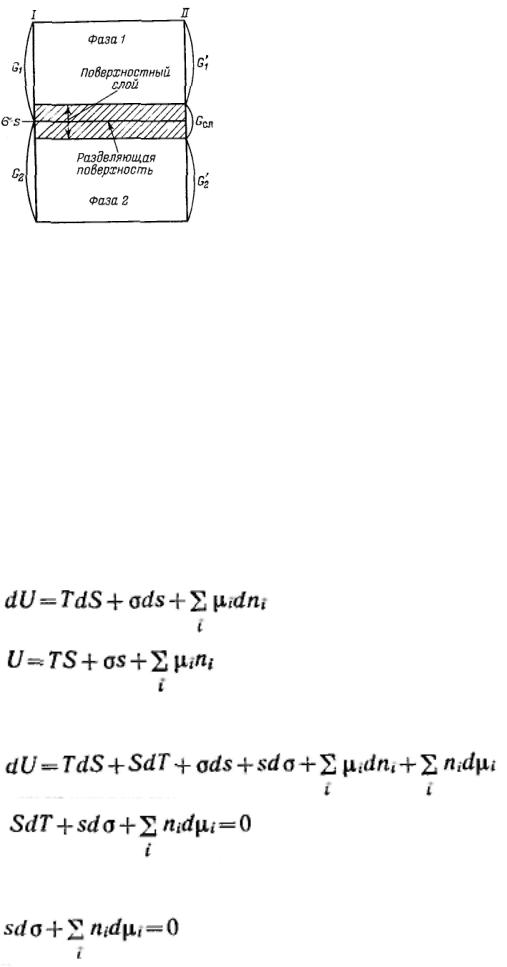
Чтобы не определять границы поверхностного слоя (поверхности разрыва по Гиббсу), Гиббс предложил относить все изменения термодинамических параметров в слое в сравнении с параметрами объемной фазы к разделяющей поверхности, не имеющей объема или толщины (метод избыточных величин Гиббса). При таком рассмотрении поверхность характеризуется избыточными термодинамическими параметрами, непосредственно отражающими проявление поверхностной энергии. Объемные фазы считаются однородными вплоть до разделяющей поверхности. В соответствии с методом избыточных величин энергия Гиббса системы равна сумме энергий ГиббсаG1 и G2 объемных фаз 1, 2 и поверхностной энергии
Гиббса σs, которая является избыточной: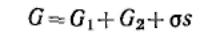
Характеристика величины адсорбции определяющася избытком вещества в поверхностном слое определенной толщины по сравнению с его количеством в таком же объеме фазы, также отнесенным к единице площади поверхности или единице массы адсорбента, называется гиббсовской адсорбцией и обозначается буквой гамма Г (метод избыточных величин Гиббса). Объединенное уравнение первого и второго начал термодинамики для внутренней энергии поверхности с учетом поверхностной и химической энергии имеет вид (объем поверхностного слоя равен нулю)
Так как внутренняя энергия поверхности пропорциональна экстенсивным величинам, то и ее полный дифференциал от тех же переменных запишется следующим образом:
Подставляя значение dU, получим:
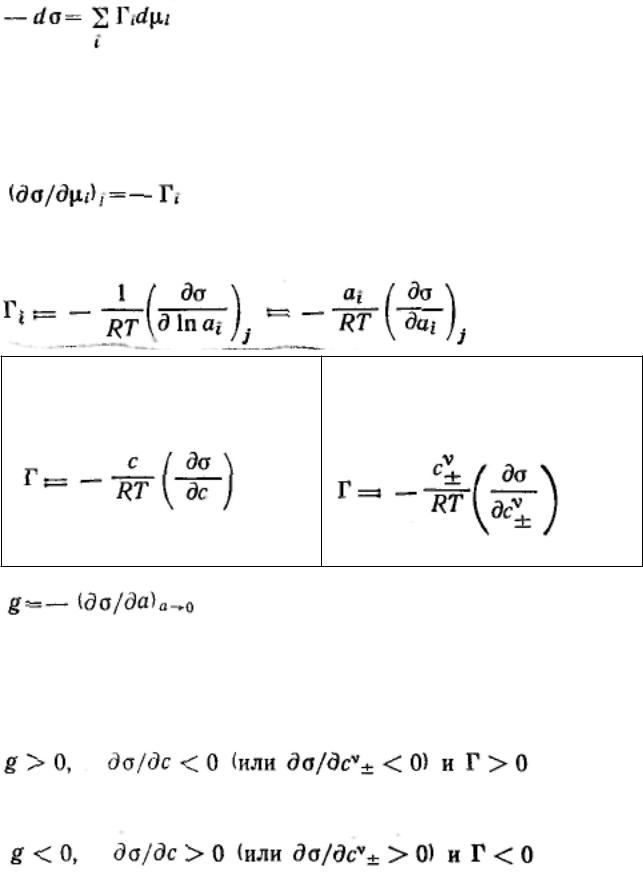
Для условия постоянства температуры это соотношение принимает вид
Разделив полученное уравнение на площадь поверхности, получим:
Данное уравнение называют фундаментальным адсорбционным уравнением Гиббса. Для адсорбции одного конкретного вещества при постоянных химических потенциалах
других веществ полученное уравнение можно записать относительно частной производной для данного компонента:
Принимая во внимание, что 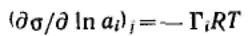 Для гиббсовской адсорбции это выражение принимает вид
Для гиббсовской адсорбции это выражение принимает вид
Для растворенного вещества это выражение переходит в широко используемые адсорбционные уравнения Гиббса для неэлектролитов
и для электролитов при их диссоциации в полярной фазе и отсутствии ее в поверхностном слое (при неполярной второй фазе):
Общее определение поверхностной активности дается соотношением:
которое справедливо как для неэлектролитов, так и для электролитов.
Поверхностная активность, как и гиббсовская адсорбция, может быть положительной и отрицательной. Абсолютное значение и ее знак зависят от природы как адсорбируемого вещества, так и среды (растворителя). Если с увеличением концентрации вещества поверхностное натяжение на границе раздела фаз понижается, то такое вещество называют поверхностно-активным. Для таких веществ
Вещества, повышающие поверхностное натяжение на границе раздела фаз с увеличением концентрации, называют поверхностно-инактивными. Для них
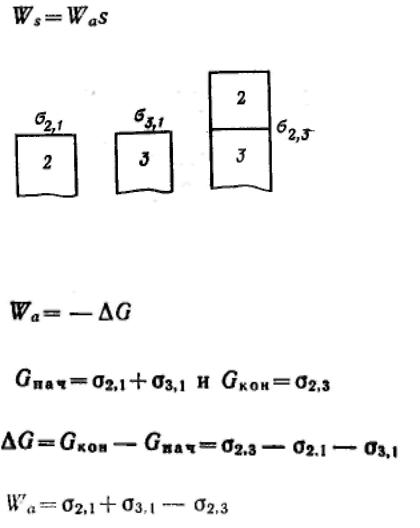
4.Адгезия и смачивание, определения. Уравнение Дюпре для работы адгезии. Угол смачивания и уравнение Юнга. Уравнение Дюпре-Юнга для работы адгезии. Влияние ПАВ на адгезию и смачивание.
Адгезия, смачивание и растекание относятся к межфазным взаимодействиям, которые происходят между конденсированными фазами. Межфазное взаимодействие, или взаимодействие между приведенными в контакт поверхностями конденсированных тел разной природы, называют адгезией (прилипанием).
Работа адгезии Wа, характеризующая прочность адгезионной связи, определяется работой обратимого разрыва адгезионной связи, отнесенной к единице площади. Ома измеряется в тех же единицах, что и поверхностное натяжение (Дж/м2). Полная работа адгезии, приходящаяся на всю площадь контакта тел s, равна
Чтобы получить соотношение между работой адгезии и поверхностными натяжениями взаимодействующих компонентов, представим себе две конденсированные фазы 2 и 3, имеющие поверхности на границе с воздухом 1, равные единице площади.
Для начального и конечного состояний системы имеем
Изменение энергии Гиббса системы в процесс адгезии равно
или
Это уравнение Дюпре. Оно отражает закон сохранения энергии при адгезии.
Условие растворения: 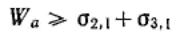 Смачивание— это поверхностное явление, заключающееся во взаимодействии жидкости с
Смачивание— это поверхностное явление, заключающееся во взаимодействии жидкости с
твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздухом). Степень смачивания количественно характеризуется косинусом краевого угла (угла смачивания), или просто краевым углом (углом смачивания).
У

голθ, который образован касательными к межфазным поверхностям, ограничивающим смачивающую жидкость, имеющий вершину на линии раздела трех фаз, называется краевым углом, или углом смачивания.
Так как поверхностное натяжение можно рассматривать как энергию, приходящуюся на единицу площади, или как силу, действующую на единицу длины, то все рассмотренные составляющие поверхностной энергии можно выразить с помощью векторов сил. При равновесии между ними соблюдается следующее соотношение:
Полученное соотношение называется законом Юнга.
Чем меньше угол Θ и соответственно больше cos θ, тем лучше смачивается поверхность. При остром угле Θ, т. е. при cos θ>0, поверхность считают хорошо смачиваемой данной жидкостью. Если угол θ тупой, т. е. соs θ<0, то по отношению к данной жидкости поверхность смачивается плохо (часто говорят «не смачивается»).
Уравнение Дюпре самостоятельно почти не используется для расчета работы адгезии из-за трудности определения поверхностного натяжения твердых тел на границе с газом (воздухом) и жидкостью. Удобную для расчета этой величины форму имеет соотношение, получаемое в результате сочетания уравнения Дюпре с законом Юнга
Если разность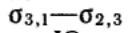 в уравнении Дюпре заменить ее выражением нз закона Юнга
в уравнении Дюпре заменить ее выражением нз закона Юнга
,получим
Это уравнение называют уравнением Дюпре-Юнга; оно связывает работу адгезии с краевым углом и позволяет рассчитать работу адгезии, если известны поверхностное натяжение жидкости и краевой угол. Обе эти величины можно сравнительно легко определить экспериментально.
Введение ПАВ уменьшает работу когезии (поверхностное натяжение) жидкости а значит, как следует из уравнения Дюпре-Юнга, увеличивает смачивание. Лучше смачивает та жидкость, которая имеет меньшее поверхностное натяжение или работу когезии.
5.Правило фаз Гиббса и дисперсность. Влияние кривизны поверхности (дисперсности) на внутреннее давление тел (вывод и анализ уравнения Лапласа). Капиллярные явления (уравнение Жюрена).
Дисперсность является самостоятельным и полноправным термодинамическим параметром системы, а для дисперсных систем правило фаз Гиббса принимает следующий вид:
F – количество степеней свободы, К – количество компонентов, Ф – количество фаз.
