билеты 19

P

Билет 4

1.Количественные характеристики пористых материалов: пористость, удельная поверхность, размер пор. Пористые тела корпускулярной, кристаллической и губчатой структуры, методы их получения. Классификации пор по Дубинину и теория адсорбции.

Пористые тела — это твердые тела, внутри которых имеются поры, обусловливающие наличие внутренней межфазной поверхности. Поры могут быть заполнены газом или жидкостью.

Высокодисперсные пористые неорганические материалы, в частности, адсорбенты и катализаторы, получают в основном двумя методами. Один из них заключается в синтезе гидрозоля с последующей его коагуляцией для образования геля; гель высушивают. Частицы дисперсной фазы (корпускулы) в результате этих операций срастаются с образованием твердого каркаса. Так как частицы золя высокодисперсны, то получаемый пористый материал имеет большую удельную поверхность. Таким методом получают адсорбенты корпускулярной структуры.

Второй метод получения высокодисперсных пористых адсорбентов и катализаторов заключается в обработке крупнопористых материалов агрессивными газами или жидкостями. При такой обработке получаются пористые тела губчатой структуры.

Наибольшее распространение получила классификация пористых тел, предложенная M. M. Дубининым. По этой классификации за основу приняты размеры пор и механизм протекающих в них адсорбционных процессов. По классификации M. M. Дубинина пористые тела делятся на макропористые, переходнопористые, микропористые в

зависимости от линейного размера, под которым понимают полуширину для щелевидной поры или радиус для сферической или цилиндрической поры.

Макропористые тела имеют поры радиусом больше 100,0 — 200,0 нм, удельная поверхность макропористых тел находится в пределах 0,5 — 2 м2/г. В связи с тем, что такие поры намного больше адсорбируемых молекул, то их стенки по сравнению с молекулами можно рассматривать как ровные поверхности, поэтому для макропористых тел применима обобщенная теория адсорбции Ленгмюра.

Переходнопористые тела (или капиллярно-пористые, или мезопористые) имеют размеры пор в пределах от 1,5 до 100,0 — 200,0 нм их удельная поверхность составляет от 10 до 500 м2/г. Ha стенках этих пор при малых давлениях происходит полимолекулярная адсорбция паров, которая с увеличением давления заканчивается капиллярной конденсацией.

Микропористые тела обладают порами, соизмеримыми с размерами адсорбируемых молекул. Радиусы пор лежат в пределах от 0,5 до 1,5 нм. Удельная поверхность таких тел 500

— 1000 м2/г и выше. Отличительной чертой микропор является настолько близкое

расположение противоположных стенок, что их поля поверхностных сил перекрываются и они действуют во всем объеме микропор.

Одной из основных характеристик пористой структуры тела является пористость —

отношение объема пор Vп к общему объему тела Vобщ: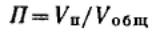

Если принять, что поры в пористых телах и порошках имеют правильную форму, то их размеры можно оценить, зная пористость и удельную поверхность:

Для определения пористости и удельной поверхности пористых тел широко используются адсорбционные методы.

2.Моделирование реологических свойств тел, модель и уравнение Бингама. Кривые течения и вязкости жидкообразной и твердообразной систем с коагуляционной структурой. Ползучесть, предел текучести.

Реологические модели Существуют три основных случая механического поведения:

1)упругость;

2)вязкость;

3)пластичность.

Комбинируя эти процессы и реологические модели процессов, можно получить более сложные модели, которые будут описывать реологические свойства самых различных систем. Во всех случаях каждая комбинация будет рассматриваться в определенном режиме деформирования характерном для этого явления, в котором будут проявляться свойства моделей по сравнению со свойствами ее элементов.

1. Модель Максвелла – последовательное соединение упругости и вязкости. Последовательное соединение таких элементов может означать по третьему закону Ньютона, что на две составные части модели будут действовать одинаковые силы (напряжение сдвига τ), а деформации упругости (γG) и вязкости (γη) могут быть сложены:

γ = γG + γ?,

где g – общая деформация.

В этой модели возможно быстрое деформирование до определенного значения и сохранение ее на постоянном уровне. При больших значениях времени такой тип системы может быть близок по свойству к жидкости, но при приложении напряжения сдвига система может вести себя как упругое твердое тело.

2. Модель Кельвина – параллельное соединение упругости и вязкости. В такой модели деформации обоих элементов могут быть одинаковыми, а напряжения сдвига будут суммироваться. При постоянном воздействии напряжения модель Кельвина ведет себя иначе. Вязкий элемент не может позволить реализоваться немедленно деформации упругого элемента. Тогда общая деформация может постепенно развиваться во времени:

Это уравнение соответствует постепенно замедляющейся деформации. Снятие общего напряжения происходит за счет энергии, накопленной упругим элементом, здесь происходит процесс деформации эластичного тела, и рассеивание энергии происходит на вязком элементе. Пример таких моделей: затухание колебаний, прежде всего механических в резине. 3. Ввод в систему нелинейного элемента. Получается модель, описывающая возникновение внутренних напряжений при параллельном сочетании упругого элемента и сухого трения.

Если в системе приложенное напряжение превышает предел текучести, то возникает деформация, которая может быть обусловлена накоплением энергии упругого элемента. 4. Модель Бингама – параллельное соединение вязкого ньютоновского элемента и сухого

кулоновского элемента трения. Так как элементы одинаковы, то и их деформации тоже будут одинаковыми, а напряжения будут складываться. Причем напряжение на кулоновском элементе не может превышать предельного значения напряжения сдвига.

Из этого следует вывод, что скорость деформации, которая описывается вязким элементом, должна быть пропорциональна разности действующего напряжения и предельного напряжения сдвига.

При усложнении реологических моделей усложняется математический аппарат описания деформаций, поэтому все виды напряжений стараются сводить к более простым моделям. Одним из методов облегчения таких задач служит использование т. н. электромеханических аналогий, т. е. получение реологических моделей с помощью электрических цепей.

3.Найдите графически время половинной коагуляции и начальную концентрацию частиц по изменению общей концентрации частиц лиофобной дисперсной системы:

P

Билет 5

1.Адсорбция на пористых адсорбентах. Теория капиллярной конденсации. Капиллярно-конденсационный гистерезис. Расчет и назначение интегральной и дифференциальной кривых распределения объема пор по размерам.

Удерживание газов и паров пористыми телами, т. е. их адсорбционная способность, зависят как от природы взаимодействующих тел, так и от структуры пористого тела. Если структурный фактор для макропористых адсорбентов имеет малое значение, то уже для переходнопористых тел его роль резко возрастает. Это обусловлено в первую очередь проявлением капиллярных сил. Чем меньше размер пор, тем сильнее капиллярное удерживание адсорбата. В противном случае (если поверхность не смачивается) наблюдается капиллярное выталкивание вещества из пор, адсорбция на несмачиваемых телах минимальна и возможна только на ровной поверхности и в крупных порах.

Адсорбция на переходнопористых телах происходит в основном по механизму капиллярной конденсации. Капиллярная конденсация начинает проявляться при определенной степени заполнения адсорбента или при определенном значении давления пара, характерном для данной системы.

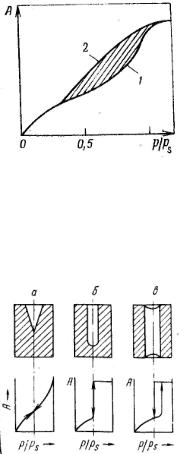
Для адсорбентов с переходными порами характерна изотерма адсорбции с петлей капиллярно-конденсационного гистерезиса. Адсорбции соответствует нижняя кривая, а десорбции — верхняя. При малых давлениях, когда не происходит капиллярная конденсация, гистерезиса не наблюдается. Начало появления гистерезиса зависит от природы адсорбента и адсорбата.

Конденсация на стенках цилиндрической поры приводит к уменьшению диаметра поры, что вызывает ее мгновенное заполнение при давлении, отвечающем началу конденсации. На концах поры образуются сферические мениски жидкости. Десорбция может начаться только при давлении, соответствующем радиусам кривизны этих менисков. Таким образом,

опорожнение капилляра происходит при меньшем давлении, чем его заполнение. Этим объясняется появление петли капиллярно-конденсационного гистерезиса.

Капиллярная конденсация описывается уравнением Кельвина, в которое входит радиус кривизны мениска, и это позволяет использовать его для расчета функции распределения пор по размерам.

Метод расчета функций распределения частиц (пор) по размерам заключается в построении интегральных и дифференциальных кривых распределения.

Для пористых тел принято характеризовать распределение пор по их радиусам, поэтому интегральная кривая распределения выражает зависимость общего объема пор от их радиуса:

.

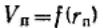Другой функцией распределения для данного пористого тела является зависимость f(rп) или dVп/drп от rп, которая называется дифференциальной кривой распределения. Она более четко и наглядно характеризует полидисперсность системы.

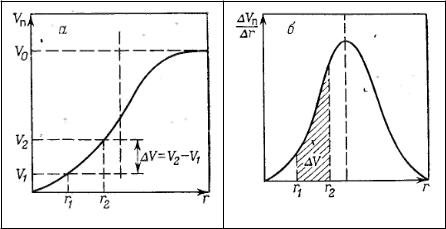
Для получения кривых распределения по методу капиллярной конденсации используют десорбционную ветвь изотермы адсорбции, так как для всех без исключения пор она соответствует сферическим менискам, радиусы которых принимают за радиусы пор.

2.Лиофобные дисперсные системы. Факторы агреативной устойчивости лиофобных систем. Быстрая и медленная коагуляция. Кинетика коагуляций по Смолуховскому (вывод уравнения). Определение константы скорости и времени половинной коагуляции. Зависимость числа частиц разного порядка от времени.

Все дисперсные системы в зависимости от механизма процесса их образования по классификации П. А. Ребиндера подразделяют на лиофильные, которые получаются при самопроизвольном диспергировании одной из фаз (самопроизвольное образование гетерогенной свободнодисперсной системы), и лиофобные, получающиеся в результате диспергирования и конденсации с пересыщением (принудительное образование гетерогенной свободноднсперсной системы).

Различают следующие термодинамические и кинетические факторы устойчивости дисперсных систем:

1.Электростатический фактор заключается в уменьшении межфазного натяжения вследствие возникновения двойного электрического слоя на поверхности частиц в соответствии с уравнением Липпмана.

2.Адсорбционно-сольватный фактор состоит в уменьшении межфазного натяжения при взаимодействии частиц дисперсной фазы со средой (благодаря адсорбции и сольватации)

3.Энтропийный фактор, как и первые два относится к термодинамическим. Он дополняет первые два фактора и действует в системах, в которых частицы или их поверхностные слои участвуют в тепловом движении.

4.Структурно-механический фактор является кинетическим. Его действие обусловлено тем, что на поверхности частиц имеются пленки, обладающие упругостью и механической прочностью, разрушение которых требует затраты энергии и времени.

5.Гидродинамический фактор снижает скорость коагуляции благодаря изменению вязкости среды и плотности дисперсной фазы и дисперсионной среды.

6.Смешанные факторы наиболее характерны для реальных систем. Обычно агрегативная устойчивость обеспечивается несколькими факторами одновременно.

Коагуляция протекает в термодинамически неустойчивых (лиофобных) дисперсных системах, и об агрегативной устойчивости таких систем судят по скорости коагуляции. Смолуховским была рассмотрена кинетика коагуляции монодисперсных золей со сферическими частицами, которые сталкиваются между собой в результате броуновского движения. Критическое расстояние, на котором осуществляется взаимодействие между частицами, принято приблизительно равным сумме радиусов частиц, что соответствует непосредственному их контакту. Согласно представлениям Смолуховского при коагуляции

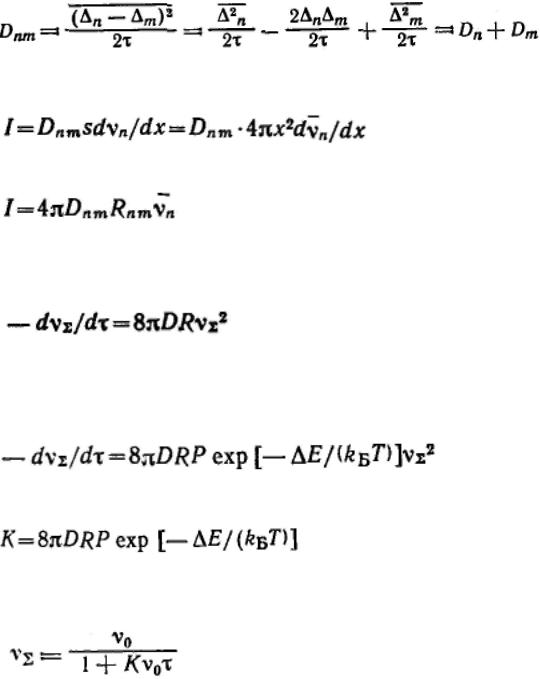
происходят взаимодействия только между двумя частицами, так как вероятность одновременного столкновения большого числа частиц очень мала. Таким образом, сталкиваются частицы одиночные, образуя двойные, одиночные с двойными, двойные друг с другом, тройные с одиночными и т. д. Такое представление процесса коагуляции позволяет формально применить к нему теорию бимолекулярных химических реакций. Относительное смещение двух частиц. n— m с коэффициентом относительной диффузии Dnm связано законом Эйнштейна — Смолуховского:

В соответствии с первым законом Фика поток через сферическую поверхность s выражается уравнением

Интегрируя уравнение данное после разделения переменных в пределах от Rnm до ∞ и соответственно от 0 до νn, получим:

Данное уравнение отражает также число столкновении на данной стадии процесса коагуляции, т. е. число частиц, сталкивающихся в единицу времени с одной центральной частицей. Общее число столкновений между частицами в системе в единицу времени в данный момент составляет .

Чтобы рассчитать скорость уменьшения числа частиц в результате коагуляции, т. е. скорость коагуляции, необходимо принять, что все столкновения приводят к агрегации. Необходимо учесть стерический множитель P, учитывающий благоприятные пространственные расположения частиц при столкновении, их форму, размеры. Тогда скорость коагуляции в данный момент времени составит:

Сравнение с уравнением для скорости бимолекулярной реакции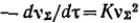 , показывает, что константа скорости коагуляции выражается следующим соотношением:

Общее число частиц в результате коагуляции уменьшается. Чтобы определить, каким оно будет через время τ, необходимо провести интегрирование в пределах от ν∑ = ν0 при τ = 0 до ν∑ при τ:

Константу скорости коагуляции теоретически определить трудно, поэтому Смолуховский ввел понятие времени (периода) половинной коагуляции θ — времени коагуляции, в течение которого общая концентрация частиц уменьшается до половины от начальной концентрации первичных (единичных) частиц. Из уравнения общего числа частиц следует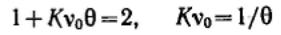: и .

и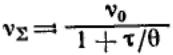

Общее число частиц ν∑ в единице объема системы представляет собой уменьшающуюся в процессе коагуляции сумму частиц всех порядков:

Этот ряд является суммой геометрической прогрессии со знаменателем

Отсюда легко определить число частиц каждого порядка (m-мерных):

Согласно теории кинетики коагуляции различают быструю и медленную коагуляцию. Для такого разделения можно воспользоваться уравнением константы скорости коагуляции. При быстрой коагуляции все столкновения частиц эффективны, т. е. приводят к слипанию частиц. При медленной коагуляции это утверждение не соблюдается.

3.Коэффициент диффузии частиц золя серебра в воде при 25ᵒС равен P3,18*10−6 м2/ сутки. Рассчитайте дисперность частиц золя и их среднеквадратичный сдвиг за 10 с. Вязкость воды при 25ᵒС равна P8,94*10−4 Па с.

P

Билет 6

1.Теopия полимолекулярной адсорбции БЭТ: исходные положения, вывод уравнения изотермы и его анализ. Линейная форма уравнения БЭТ. Определение удельной поверхности адсорбентов, катализаторов и других пористых тел.

Уравнение Ленгмюра можно использовагь только при условии, что адсорбция вещества сопровождается образованием мономолекулярного слоя.

В большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и влияние поверхностных сил может распространяться на второй, третий и последующие адсорбционные слои, в результате проходит полимолекулярная адсорбция.

Современная форма уравнения полимолекулярной адсорбции — основного уравнения обобщенной теории Ленгмюра — была предложена Брунауэром, Эмметом и Теллером.

В этой теории дополнительным допущением к тем, которые были положены в основу вывода уравнения изотермы Ленгмюра, является представление об образовании на поверхности адсорбента «последовательных комплексов» адсорбционных центров с одной, двумя, тремя и т. д. молекулами адсорбата. Тогда процесс адсорбции можно представить в виде последовательных квазихимических реакций:

Константы равновесия этих реакций соответственно равны

Обозначим:

Общее число активных центров на адсорбенте, или емкость монослоя, будет равна

После ряда вычислений с применением теории рядов, окончательно получим:

Данное соотношение является основным уравнением обобщенной теории Ленгмюра и называется уравнением полимолекулярной адсорбции БЭТ.

При обработке экспериментальных результатов уравнение БЭТ обычно используют в

линейной форме: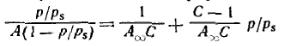

Оно позволяет графически определить оба постоянных параметра A∞ и С:

Экспериментальное определение A∞ позволяет рассчитать удельную поверхность адсорбента

(поверхность единицы массы адсорбента): .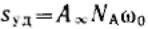

2.Лиофильные дисперсные системы. Классификация и общая характеристика ПАВ. Термодинамика и механизм мицеллобразования. Строение мицелл ПАВ в водных и углеводородных средах. Солюбизация. +

Все дисперсные системы в зависимости от механизма процесса их образования по классификации П. А. Ребиндера подразделяют на лиофильные, которые получаются при самопроизвольном диспергировании одной из фаз (самопроизвольное образование гетерогенной свободнодисперсной системы), и лиофобные, получающиеся в результате диспергирования и конденсации с пересыщением (принудительное образование гетерогенной свободноднсперсной системы).

Наличие гидрофильной и олеофильной частей у молекул ПАВ является характерной отличительной особенностью их строения. По способности к диссоциации в водных растворах поверхностно-активные вещества делят на ионогенные и неионогенные. В свою очередь ионогенные ПАВ подразделяют на анионные, катионные и амфолитпые (амфотерные).

1)Анионные ПАВ диссоциируют в воде с образованием поверхностно-активного аниона.

2)Катионные ПАВ диссоциируют в воде с образованием поверхностно-активного катиона.

3)Амфотерные ПАВ содержат две функциональные группы, одна из которых имеет кислый, а другая основный характер, например карбоксильную и аминную группы. В зависимости от рН среды амфолитные ПАВ проявляют анионоактивные или катионоактивные свойства.

Все ПАВ относительно поведения их в воде делят на истинно растворимые и коллоидные. Истинно растворимые ПАВ в растворе находятся в молекулярно-дисперсном состоянии вплоть до концентраций, соответствующих их насыщенным растворам и разделению системы на две сплошные фазы.

Главной отличительной особенностью коллоидных ПАВ является способность образовывать термодинамически устойчивые (лиофильные) гетерогенные дисперсные системы (ассоциативные, или мицеллярные, коллоиды). К основным свойствам коллоидных ПАВ, обусловливающим их ценные качества и широкое применение, относятся высокая поверхностная активность; способность к самопроизвольному мицеллообразованию — образованию лиофильных коллоидных растворов при концентрации ПАВ выше некоторого определенного значения, называемого критической концентрацией мицеллообразования (KKM); способность к солюбилизации — резкому увеличению растворимости веществ в растворах коллоидных ПАВ вследствне их «внедрения» внутрь мицеллы; высокая способность стабилизировать различные дисперсные системы.

При концентрациях выше KKM молекулы ПАВ собираются в мицеллы (ассоциируют) и раствор переходит в мицеллярную (ассоциативную) коллоидную систему.

Под мицеллой ПАВ понимают ассоциат дифильных молекул, лиофильные группы которых обращены к соответствующему растворителю, а лиофобные группы соединяются друг с другом, образуя ядро мицеллы. Число молекул, составляющих мицеллу, называют числом ассоциации, а общую сумму молекулярных масс молекул в мицелле, или произведение массы мицеллы на число Авогадро, — мицеллярной массой. Определенное ориентирование дифильных молекул ПАВ в мицелле обеспечивает минимальное межфазное натяжение на границе мицелла — среда.

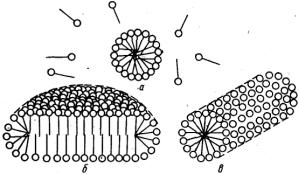
При концентрациях ПАВ в водном растворе, несколько превышающихKKM, согласно представлениям Гартли образуются сферические мицеллы (мицеллы Гартли). Внутренняя часть мицелл Гартли состоит из переплетающихся углеводородных радикалов, полярные группы молекул ПАВ обращены в водную фазу. Диаметр таких мицелл равен удвоенной длине молекул ПАВ. Число молекул в мицелле быстро растет в пределах узкого интервала концентраций, а при дальнейшем увеличении концентрации практически не изменяется, а увеличивается число мицелл. Сферические мицеллы могут содержать от 20 до 100 молекул и более.

При увеличении концентрации ПАВ мицеллярная система проходит ряд равновесных состояний, различающихся по числам ассоциации, размерам и форме мицелл. При достижении определенной концентрации сферические мицеллы начинают взаимодействовать между собой, что способствует их деформации. Мицеллы стремятся принять цилиндрическую, дискообразную, палочкообразную, пластинчатую форму. Мицеллообразование в неводных средах, как правило, является результатом действия сил притяжения между полярными группами ПАВ и взаимодействия углеводородных радикалов с молекулами растворителя. Образующиеся мицеллы обращенного вида содержат внутри негидратированные или гидратированные полярные группы, окруженные слоем из углеводородных радикалов. Число ассоциации (от 3 до 40) значительно меньше, чем для водных растворов ПАВ. Как правило, оно растет с увеличением углеводородного радикала до определенного предела.

Критическая концентрация мицеллообразования — важнейшая характеристика растворов ПАВ. Она зависит прежде всего от строения углеводородного радикала в молекуле ПАВ и характера полярной группы, наличия в растворе электролитов и неэлектролитов, температуры и других факторов.

3.Рассчитайте численную концентрацию золя Al2O3, если известно, что его массовая концентрация равна 0,3 кг/м3. Коэффициент диффузии частиц 2·10-6 м2/сутки,