билеты 19

распределения, воспользуемся данным соотношением (iдиф = iсед), учтя, что

J

и заменив x на h (расстояние по высоте):

J

После разделения переменных получим:

J

Интегрируя в пределах от ν0 до νh и соответственно от h = 0 до h, найдем:

J илиJ

Это уравнение носит название гипсометрического закона (от лат. hypsos — высота). Если сравнить седиментацию при наличии диффузии и без нее, то обращает на себя внимание различие факторов, обеспечивающих устойчивость дисперсных систем к осаждению — седиментационную устойчивость. Эти факторы позволяют различать кинетическую седиментационную устойчивость (КСУ) и термодинамическую седиментационную устойчивость (ТСУ).

Мерой кинетической седиментационной устойчивости является величина, обратная константе седиментации:

J

Мерой ТСУ является гипсометрическая высота. Ее удобнее определить как высоту he, на протяжении которой концентрация дисперсной фазы изменяется в е раз.

J

Данная формула показывает, что гипсометрическая высота и соответственно термодинамическая седиментационная устойчивость тем больше, чем меньше размер частиц и разность между плотностями частиц и среды. Вязкость не влияет на ТСУ, в то (же время повышение температуры способствует устойчивости, так как усиливается тепловое движение. Кинетическая же седиментационная устойчивость с повышением температуры обычно снижается в связи с уменьшением вязкости среды

3.Электрофорез дисперсии бентонитовой глины происходит при следующих условиях: расстояние между электродами 32 см, напряжение 120 В, за 15 минут частицы переместились на 11 мм к аноду. Рассчитайте ζ-потенциал, учитывая, что ε = 78,2, а η = 10-3 Па·с.

P

Билет 22

1.Влияние дисперсности на термодинамическую реакционную способность. Вывод уравнения капиллярной конденсации Кельвина. Влияние дисперсности на растворимость, константу равновесия химической реакции и температуру фазового перехода.

Термодинамическая реакционная способность характеризует способность вещества переходить в какое-либо иное состояние, например переходить в другую фазу, вступать в химическую реакцию. Она указывает на удаленность данного состояния вешества или системы компонентов от равновесного состояния при определенных условиях. Термодинамическая реакционная способность определяется химическим сродством, которое можно выразить изменением энергии Гиббса или разностью химических потенциалов. Реакционная способность зависит от степени дисперсности вещества, изменение которой может приводить к сдвигу фазового или химического равновесия.

Соответствующее приращение энергии Гиббса dGд (благодаря изменению дисперсности) можно представить в виде объединенного уравнения первого и второго начал термодинамики:

Для индивидуального вещества V=Vм и при Т=const имеем:

Подставляя в это уравнение соотношение Лапласа, получим: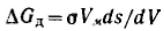

для сферической кривизны: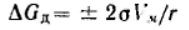 Если рассматривается переход вещества из конденсированной фазы в газообразную, то

энергию Гиббса можно выразить через давление пара, приняв его за идеальный. Дополнительное изменение энергии Гиббса, связанное с изменением дисперсности,

составляет: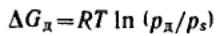

Подставляя данное выражение, получим:

Полученное соотношение называется уравнением Кельвина (уравнение капиллярной конденсации).(pд-равновесное давление адсорбата, ps-насыщ давление пара адсорбата) Для неэлектролитов его можно записать следующим образом:

Из этого уравнения видно, что с увеличением дисперсности растворимость растет, или химический потенциал частиц дисперсной системы больше, чем у крупной частицы, на величину 2σV/r.

Степень дисперсности может влиять также на равновесие химической реакции:

Сувеличением дисперсности повышается активность компонентов, а в соответствии с этим изменяется константа химического равновесия в ту или другую сторону, в зависимости от степени дисперсности исходных веществ и продуктов реакции.

Сизменением дисперсности веществ изменяется температура фазового перехода. Количественная взаимосвязь между температурой фазового перехода и дисперсностью вытекает из термодинамических соотношений.

Для фазового перехода:,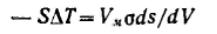

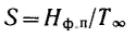
Для сферических частиц: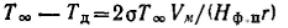

Видно, что с уменьшением размера частиц г температуры плавления и испарения вещества уменьшаются (Hф.п.>0).

2.Природа броуновского движения, понятие и определение среднеквадратичного сдвига по выбранному ?. Взаимосвязь между среднеквалратичным сдвигом и коэффициентом диффузии (вывод закона Эйнштейна-Смолуховского). Экспериментальная проверка закона.

Основой доказательства теплового молекулярного движения в телах явилось обнаруженное английским ботаником Робертом Броуном в 1827 г. с помощью микроскопа непрерывное движете очень мелких частичек — спор папоротника (цветочной пыльцы), взвешенных в воде. Более крупные частицы находились в состоянии постоянного колебания около положения равновесия. Колебания и перемещения частиц ускорялись с уменьшением их размера и повышением температуры и не были связаны с какими-либо внешними механическими воздействиями.

Теоретически обоснованная интерпретация броуновского движения — участие частиц дисперсной фазы ультрамикрогетерогенных систем в тепловом движении — была дана независимо друг от друга Эйнштейнии (1905 г.) и Смолуховским (1906 г.).

Проведенными исследованиями была окончательно доказана природа броуновского движения. Молекулы среды (жидкости или газа) сталкиваются с частицей дисперсной фазы, в результате чего она получает огромное число ударов со всех сторон.

Эйнштейн и Смолуховский для количественного выражения броуновского движения частиц ввели представление о среднем сдвиге частицы. Если при наблюдении движения частицы

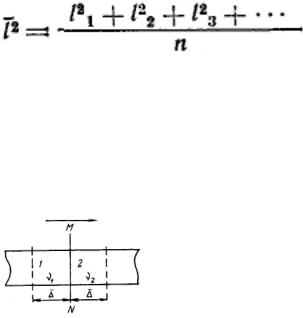
золя под микроскопом через определенные равные промежутки времени отмечать ее местонахождение, то можно получить ее траекторию движения. Так как движение происходит в трехмерном пространстве, то квадрат среднего расстояния, проходимого

частицей за любой промежуток времени, равен.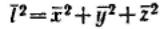

Под микроскопам наблюдают проекцию смещения частицы на плоскость за какое-то время,

поэтому .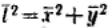

При равновероятных отклонениях частицы ее направление будет находиться между направлениями x и у, т. е. под углом 45° к каждой координате. Отсюда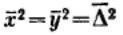или

.

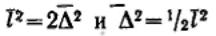Из-за равновероятных отклонений среднеарифметическое значение сдвигов равно нулю. Поэтому используются среднеквадратичные расстояния, проходимые частицей:

Эйнштейн и Смолуховский, постулируя единство природы броуновского движения и теплового движения, установили количественную связь между средним сдвигом частицы (называемым иногда амплитудой смещения) и коэффициентом диффузии D.

Если броуновское движение является следствием теплового движения молекул среды, то можно говорить о тепловом движении частиц дисперсной фазы. Это означает, что дисперсная фаза, представляющая собой совокупность числа частиц, должна подчиняться тем же статистическим законам молекулярно-кинетической теории, приложимым к газам или растворам.

Для установления связи между средним сдвигом (смещением) частицы и коэффициентом диффузии представим себе трубку с поперечным сечениемS, наполненную золем, концентрация частиц которого уменьшается слева направо. В этом же направлении протекает и диффузия частиц золя (на рисуике отмечено стрелкой). Выделим по обе стороны от линии MN два малых участка 1 и 2, размеры которых в направлении диффузии равны — среднему квадратичному сдвигу за время τ. Обозначим частичную концентрацию золя в объемах этих участков соответственно через ν1 и ν2 (ν1>ν2). Хаотичность теплового движения приводит к равной вероятности переноса дисперсной фазы из обоих объемов вправо и влево от линии MN: половина частиц переместится вправо, а другая половина — влево. Количество

дисперсной фазы за время τ переместится из объема 1 вправо: 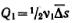,а из объема 2 влево

(в обратном направлении):.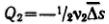

Так как |Q1| > |Q2| (ν1>ν2), то суммарное количество перенесенного вещества через плоскость MN вправо определится соотношением

.

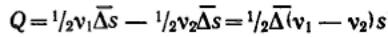Градиент концентрации по расстоянию в направлении диффузии можно выразить так:

Подставляя, получим: 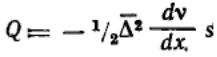Сравнивая это соотношение с первым законом диффузии Фика:

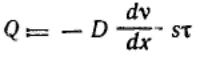,окончательно имеем:

Это уравнение выражает закон Эйнштейна — Смолуховского, в соответствии с которым квадрат среднего сдвига пропорционален коэффициенту диффузии н времени.

3.Для гидрозоля, содержащего отрицательно заряженные частицы PAssS3 порог быстрой коагуляции при добавлении PKCl равен 31 ммоль/л. Используя закон Дерягина, рассчитайте порог коагуляции для электролитов PNa2SO4, MgCl2, AlCl3

P

Билет 24

1.Адгезия и смачивание, определения. Уравнение Дюпре для работы адгезии. Угол смачивания и уравнение Юнга. Уравнение Дюпре-Юнга для работы адгезии. Влияние ПАВ на адгезию и смачивание.

Адгезия, смачивание и растекание относятся к межфазным взаимодействиям, которые происходят между конденсированными фазами. Межфазное взаимодействие, или взаимодействие между приведенными в контакт поверхностями конденсированных тел разной природы, называют адгезией (прилипанием).

Работа адгезии Wа, характеризующая прочность адгезионной связи, определяется работой обратимого разрыва адгезионной связи, отнесенной к единице площади. Ома измеряется в тех же единицах, что и поверхностное натяжение (Дж/м2). Полная работа адгезии, приходящаяся на всю площадь контакта тел s, равна

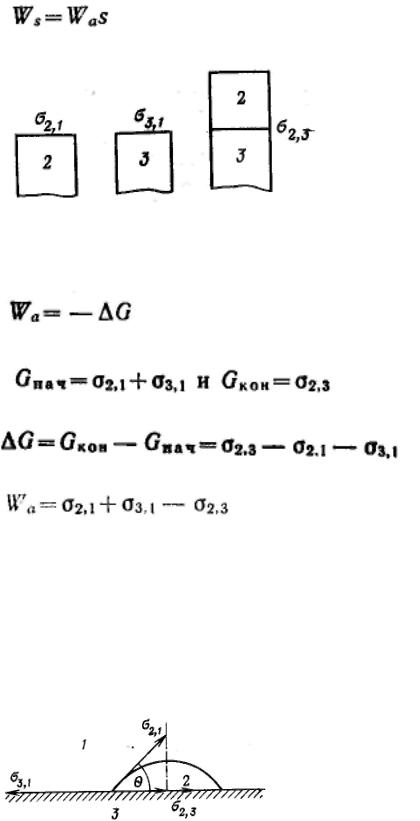
Чтобы получить соотношение между работой адгезии и поверхностными натяжениями взаимодействующих компонентов, представим себе две конденсированные фазы 2 и 3, имеющие поверхности на границе с воздухом 1, равные единице площади.

Для начального и конечного состояний системы имеем

Изменение энергии Гиббса системы в процесс адгезии равно

или

Это уравнение Дюпре. Оно отражает закон сохранения энергии при адгезии.

Условие растворения: 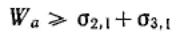Смачивание— это поверхностное явление, заключающееся во взаимодействии жидкости с

твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздухом). Степень смачивания количественно характеризуется косинусом краевого угла (угла смачивания), или просто краевым углом (углом смачивания).

У

голθ, который образован касательными к межфазным поверхностям, ограничивающим смачивающую жидкость, имеющий вершину на линии раздела трех фаз, называется краевым углом, или углом смачивания.

Так как поверхностное натяжение можно рассматривать как энергию, приходящуюся на единицу площади, или как силу, действующую на единицу длины, то все рассмотренные составляющие поверхностной энергии можно выразить с помощью векторов сил. При равновесии между ними соблюдается следующее соотношение:

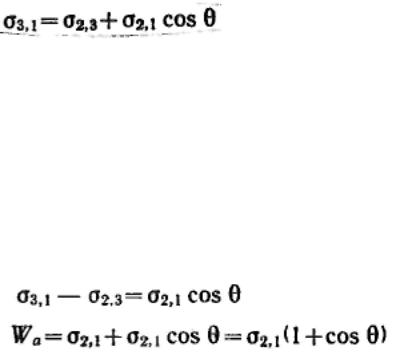
Полученное соотношение называется законом Юнга.

Чем меньше угол Θ и соответственно больше cos θ, тем лучше смачивается поверхность. При остром угле Θ, т. е. при cos θ>0, поверхность считают хорошо смачиваемой данной жидкостью. Если угол θ тупой, т. е. соs θ<0, то по отношению к данной жидкости поверхность смачивается плохо (часто говорят «не смачивается»).

Уравнение Дюпре самостоятельно почти не используется для расчета работы адгезии из-за трудности определения поверхностного натяжения твердых тел на границе с газом (воздухом) и жидкостью. Удобную для расчета этой величины форму имеет соотношение, получаемое в результате сочетания уравнения Дюпре с законом Юнга

Если разность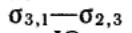в уравнении Дюпре заменить ее выражением нз закона Юнга

,получим

Это уравнение называют уравнением Дюпре-Юнга; оно связывает работу адгезии с краевым углом и позволяет рассчитать работу адгезии, если известны поверхностное натяжение жидкости и краевой угол. Обе эти величины можно сравнительно легко определить экспериментально.

Введение ПАВ уменьшает работу когезии (поверхностное натяжение) жидкости а значит, как следует из уравнения Дюпре-Юнга, увеличивает смачивание. Лучше смачивает та жидкость, которая имеет меньшее поверхностное натяжение или работу когезии.

2.Электрокинетические явления. Электрокинетический потенциал. Уравнение Смолуховского для электроосмоса и электрофореза. Эффекты, не учитываемые уравнением уравнением Смолуховского (поверхностная проводимость, электрофоретическое торможение, релаксационный эффект).

Протекание электрокинетических явлений в дисперсных системах возможно при наличии на границе раздела фаз двойного электрического слоя, имеющего диффузное строение. При относительном перемещении фаз независимо от причин, его вызвавших, происходит разрыв двойного электрического слоя по плоскости скольжения.

Потенциал, возникающий на плоскости скольжения при отрыве части диффузного слоя,

называется электрокинетическим потенциалом или ζ (дзета)-потенциалом.

Для получения наиболее простого уравнения, связывающего скорость относительного движения фаз с параметрами дисперсионной среды (вязкость, диэлектрическая проницаемость), двойного электрического слоя (ζ-потенциал) и внешнего электрического поля (напряженность), необходимо задаться некоторыми ограничениями:

1)толщина двойного электрического слоя значительно меньше радиуса пор, капилляров твердой фазы (радиуса кривизны поверхности твердой фазы);

2)слой жидкости, непосредственно прилегающий к твердой фазе, неподвижен, движение жидкости в порах твердой фазы ламинарное и подчиняется законам гидродинамики;

3)распределение зарядов в двойном электрическом слое не зависит от приложенной разности потенциалов;

4)твердая фаза является диэлектриком, а жидкость проводит электрический ток. Электрическая сила, действующая на слой жидкости dх (в расчете на единицу площади поверхности), равна

Сила трения и ее дифференциал, приходящиеся на единицу площади (согласно закону Ньютона), составляют:

При установившемся движении (в стационарном состоянии) dFэл = dFтр:

После интегрирования, окончательно получим следующее выражение для постоянной линейной скорости жидкости относительно мембраны: 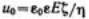Это уравнение носит название уравнения Гельмгольца — Смолуховского.

Уравнение Гельмгольца — Смолуховского чаще записывают относительно ζ-потенциала:

Это дифференциальное уравнение справедливо как для электроосмоса, так и для электрофореза, поскольку оно было выведено из баланса движущих сил процесса — электрической силы и силы трения. Отличие состоит только в выбранной системе координат. Несовпадение экспериментальных и теоретических значений электрофоретической подвижности определяется в основном двумя эффектами, неучтенными теорией Гельмгольца

— Смолуховского: релаксационным эффектом и электрофоретическим торможением. Релаксационный эффект проявляется в нарушении симметрии диффузного слоя вокруг частицы при относительном движении фаз в противоположные стороны. Возникает внутреннее электрическое поле (диполь), направленное против внешнего поля. Для восстановления равновесного состояния системы требуется некоторое время, называемое временем релаксации.

Электрофоретическое торможение обусловлено сопротивлением движению частицы обратным потоком противоионов, который увлекает за собой жидкость. Вследствие этого электрофоретическая скорость уменьшается.

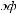
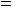
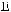
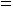
Электрофорез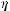: J J

Uэф- электрофоретическая подвижность

Электроосмос:

B

B

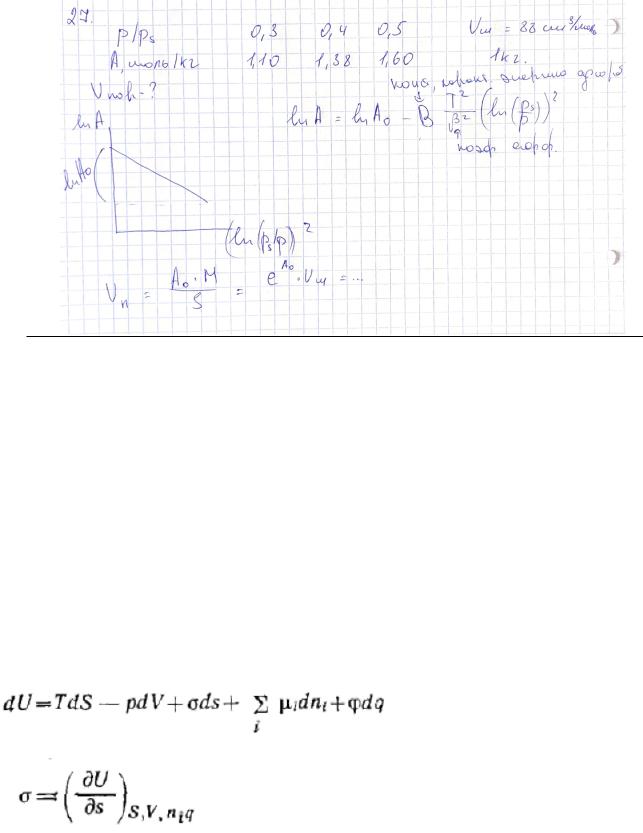
3.Используя уравнение Дубинина-Радушкевича, рассчитайте объем микропор 1кг сажи на основе данных об адсорбции паров бензола (мольный объем бензола 88,8 см3/моль):

P

Билет 26

1.Поверхностное натяжение: термодинамическое определение, физический смысл, влияние природы взаимодействующих фаз. Вывод уравнения для полной (внутренней) энергии поверхностного слоя (уравнение ГиббсаГельмгольца). Зависимость термодинамических параметров поверхности от температуры.

Есть несколько определений поверхностного натяжения:

1.Поверхностное натяжение – работа образования новой поверхности в изотермическом процессе

2.Поверхностное натяжение – сила, действующая по периметру данной поверхности, отнесенная к единице длины.

3.Поверхностное натяжение – работа переноса молекул из объема тела на поверхность.

4.Термодинамическое определение поверхностного натяжения: Термодинамическое определение поверхностного натяжения вытекает из объединенного уравнения первого и второго начал термодинамики. Запишем его для гетерогенной системы относительно изменения внутренней энергии U:

J

При постоянных S, V, ni и q имеем:

J

т. е. поверхностное натяжение есть частная производная от внутренней энергии по площади поверхности раздела фаз при постоянных энтропии, объеме, числе молей компонентов и заряде.

Так как объединенное уравнение первого и второго начал термодинамики может быть записано и относительно других термодинамических потенциалов, а именно энергии Гиббса

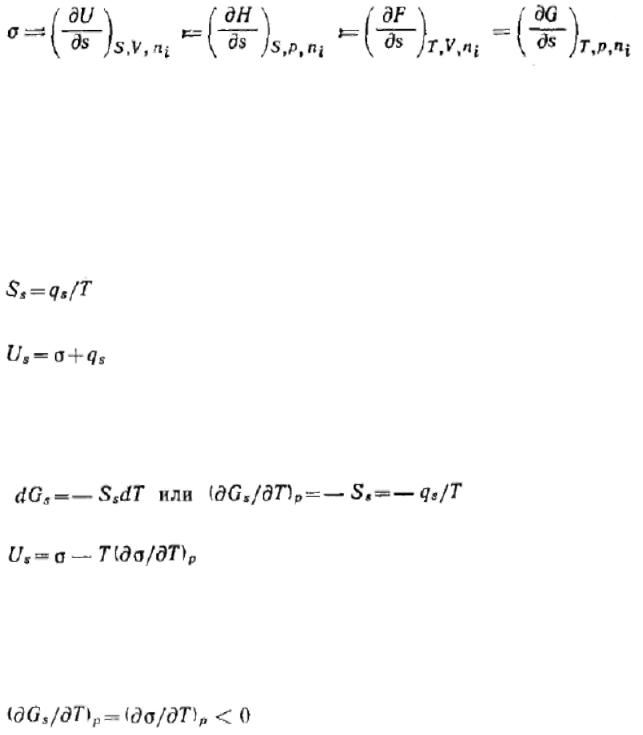
G, энергии Гельмгольца F и энтальпии Я, то при соответствующих постоянных параметрах получим:

J

Таким образом, поверхностное натяжение есть частная производная от любого термодинамического потенциала по площади межфазной поверхности при постоянных соответствующих параметрах.

Физический смысл поверхностного натяжения можно представить так: поверхностное натяжение на границе жидкости с газовой фазой – работа, расходуемая на обратимый разрыв столбика этой жидкости с поперечным сечением в 0,5 единицы площади, так как при разрыве образуется новая поверхность, равная единице площади.

Чем сильнее межмолекулярные связи в данном теле, тем больше его поверхностное натяжение на границе с газовой фазой.

В соответствии со вторым началом термодинамики избыточная энтропия равна

J

Учитывая, что Gs = σ, получим следующее выражение:

J

Из этого уравнения следует, что внутренняя энергия поверхности складывается из энергии Гиббса и теплоты образования поверхности. Для индивидуальных веществ теплота qs всегда положительна, так как при образовании поверхности теплота поглощается. Из уравнения объединенных первого и второго начала термодинамики при постоянстве всех параметров, кроме температуры, имеем:

J

Подставлям это выражение в полученные уравнения:

J

Это уравнение называется уравнением Гиббса — Гельмгольца. Оно связывает полную поверхностную энергию с энергией Гиббса (поверхностным натяжением). Из этого уравнения следует, что для определения полной поверхностной энергии необходимо знать зависимость поверхностного натяжения от температуры. Для индивидуальных веществ теплота qs всегда положительна, а это значит, что температурный коэффициент поверхностного натяжения отрицателен:

J

Таким образом, поверхностное натяжение индивидуальных веществ на границе с газом (воздухом) снижается с повышением температуры. Для большинства неполярных жидкостей эта зависимость линейная.

2.Механизмы образования двойного электрического слоя. Соотношения между электрическим потенциалом и поверхностным натяжением (вывод уравнений Липмана). Элеткокапилярные кривые и определение параметров ДЭС.

Различают три возможных механизма образования двойного электрического слоя:

1.Двойной электрический слой образуется в результате перехода ионов или электронов из одной фазы в другую (поверхностная ионизация). Например, с поверхности металла в