2.4. Метод Лагранжа для задачи со смешанными ограничениями

Как отмечалось в начале раздела, в общем случае задача нелинейного программирования содержит оба вида ограничения: равенства и неравенства, т.е.

(D, f): , (4.1)

q_i(x) ≤ b_i , i = 1,…,r

h_i(x) = d_i , i = l,…,l

Для этого случая функция Лагранжа строится в виде

, (4.2)

где _i, i = 1, …, r, _i, i = 1, … , l, - неопределенные множители Лагранжа, причем _i  , i.

Необходимые условия теоремы Куна – Таккера формируются в виде

a) L(x^*,, )/x_j = f(x^*)/x_j + q_i(x^*)/x_j +

+ h_i(x^*)/x_j = 0, j =1, …, n,

б) L(x^*,)/ _i = q_i(x^*) – b_i  0, i =1, …, r,

в) L(x^*, )/_i = h_i(x^*) – d_i = 0, i =1, …, l,

г) _i(q_i(x^*) – b_i) = 0, i =1, …, r

д) _i  0, , i =1, …, r, (4.3)

или в обозначениях градиентов соответствующих функций

а)

б) ,

в) ,

г) ^Т(q(x^*) – b) = 0,

д)   0. (4.4)

Теоретической основой решения этих систем по-прежнему является теорема Куна – Таккера. Согласно этой теореме, если в точке x* D функции q_i(x), i = 1,…, r, h_i(x), i = l,…, l, дифференцируемы, а градиенты , i = 1,…, r, i = l,…, l, линейно независимы, а сама точка x* является локальным оптимумом задачи (4.1), то существуют числа _i  0, , i =1, …, r, _i, i = 1, … , l, такие, что вместе с вектором x* удовлетворяют условиям (4.1).

Проиллюстрируем решение этих систем на следующих примерах.

Пример 1. Решить задачу

f(x) = x₁² - x₂ → min,

x₁ - 1 ≥ 0

x₁² + x₂² ≤ 26

x₁ + x₂ = 6

где q₁(x) = 1 – x₁ ≤ 0, q₂(x) = x₁² + x₂² – 26 ≤ 0, h₁(x) = x₁ + x₂ – 6 = 0.

Функция Лагранжа этой задачи имеет вид

=

= x₁² - x₂ + (1 – x₁) + ( x₁² + x₂² – 26) + (x₁ + x₂ – 6),

следовательно, необходимые условия теоремы Куна -Таккера получаются в виде

,

,

,

,

,

Путем анализа этой системы можно убедиться в том, что ее решением является точка x* = (1,5)^T, в которой имеют место

,

,

откуда следует, что .

Графическая иллюстрация решения показана на рис. 2.4.

0

x₂

A= x^* = (1, 5)^T

D

B=(5, 1)^T

x₁

x₁+ x₂ - 6=0

x₁²+ x₂² ≤ 26

Рис.2.4. Графическая иллюстрация

решения задачи.

Пример 2. Решить задачу

f(x) = -8x₁² – 10x₂² + 12x₁x₂ – 50x₁ + 80x₂ → max,

x₁ + x₂ ≤ 1

8x₁² + x₂² ≤ 2

x₁ , x₂ ≥ 0

в которой q₁(x) = 1– x₁ – x₂ ≥ 0, q₂(x) = 2 – 8x₁² – x₂² ≥ 0.

Для этой задачи функция Лагранжа равна

=

-8x₁² – 10x₂² + 12x₁x₂ – 50x₁ + 80x₂ +

₁(1– x₁ – x₂) + ₂(2 – 8x₁² – x₂²),

следовательно, необходимые условия теоремы Куна – Таккера примут вид

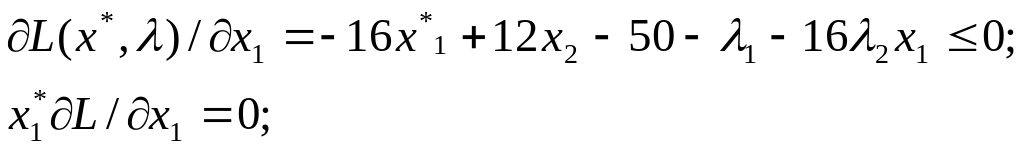
₁, ₂  0.

Аналитическое исследование этих условий приводит нас к решению x* = (0, 1)^T; = (₁, ₂)^Т = (60, 0)^T, f* = f(x^*) = 70. Уровни целевой функции, множество решений и оптимальная вершина показаны ниже на рис. 2.5.

решения.

Как отмечалось выше, после нахождения оптимального решения его обычно подвергают анализу на чувствительность, т. е. проводится исследование степени влияния параметров модели на оптимальные значения x^* и f^*. Так как целевая функция стремится к максимуму, то при увеличении значений параметров b₁ = 1, b₂ = 2 (величины ресурсов), очевидно, должны выполняться условия

x₁

x₂

8x₁² + x₂² = 2

0

D

x*= (0,1)^T

Линии

уровня ц/ф

x₁ + x₂ = 1

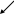
Рис.2.5. Графическая иллюстрация решения.

Для оптимального решения задачи имеют место соотношения

Нулевое значение второго множителя означает, что в точке х^* второе ограничение превращается в строгое неравенство, т.е. 8x₁^*1 + x₂^*2  2, следовательно, условие Слейтера для него выполняется.