Раздел 2. Нелинейное программирование

2.1. Математическая постановка задачи

В наиболее общей форме задача нелинейного программирования имеет вид

(D, f): , (1.1)

q_i(x) ≤ b_i , i = 1,…,r

h_i(x) = d_i , i = l,…,l

где х = (х₁, …, х_п)^Т, - вектор переменных задачи, q_i(x) ≤ b_i , i = 1,…,r – ограничения типа неравенства, h_i(x) = d_i , i = l,…, l, - ограничения типа равенства, b_i, d_i – заданные параметры, f(x) – целевая функция, - некоторое открытое подмножество Е^п, на котором определены функции f(x), q_i(x) и h_i(x)  I, D – множество допустимых решений, определяемое ограничениями задачи, т.е. D = { / q_i(x) ≤ b_i , i = 1,…,r, h_i(x) = d_i , i = l,…,l}. Решение задачи сводится к нахождению вектора х^* из D, который максимизирует или минимизирует целевую функцию f(x).

Различают локальные и глобальные решения задачи (1.1). Решение х^* D называется глобальным, если для задачи на максимум имеет место условие

. (1.2)

Если же имеет место условие

(1.3)

где = { х X /x – x^*  } - некоторая  - окрестность точки х^*, то решение х^* называется локальным.

Существуют необходимые и достаточные условия оптимальности решений (обозначим их через НДУ, НУ и ДУ, соответственно). НДУ - это условия, без выполнения которых утверждение о том, что решение х^* является оптимальным, заведомо не может быть верным (НУ), и, соответственно, при выполнении которых утверждение о том, что решение х^* является оптимальным, заведомо верно (ДУ). Процедура проверки этих условий изображена на рис. 2.1.

“претендент”

нет

нет

да

да

“ не претендует на оптимальность”

“Нужны дополнительные исследования”

“ является оптимальным решением задачи”

Рис. 2.1. «Тест» на оптимальность.

2.2. Метод Лагранжа для задачи с ограничениями типа равенства

В предположении, что присутствующие в задаче (1.1) функции f(x), q_i(x), i =1, …, m, и h_i(x), j = 1, …, l, имеют непрерывные частные производные первого порядка, задачу можно решить с помощью метода множителей Лагранжа. Задача с ограничениями типа равенства имеет вид

(D, f): . (2.1)

h_i(x) = d_i , i = l,…,l

Согласно общей теории, составляем функцию Лагранжа в виде

, (2.2)

где _i, i =1, …, l, - неопределенные множители Лагранжа. Для того чтобы точка х^* была оптимальным решением задачи (2.1), необходимо существование величин _i, i =1, …, l, удовлетворяющих условиям теоремы Куна – Таккера

L(x^*, )/x_j = f(x^*)/x_j + h_i(x^*)/x_j = 0,

j =1, …, n,

L(x^*, )/_i = h_i(x^*) – d_i = 0, i =1, …, l, (2.3)

или в терминах векторов-градиентов _xL, _L, _хf и _xh:

,

. (2.4)

В этих условиях предполагается, что градиенты _xh_i(x^*), i = 1, …, l, линейно независимы. В этом случае из первого равенства следует важное для геометрического представления условие

(2.5)

которое означает, что вектор-градиент _хf в точке х* представляется в виде линейного разложения (линейной комбинации) векторов _xh_i(x^*), i = 1, …, l, с коэффициентами разложения - _i, i =1, …, l.

Решение системы (2.2) в виде двойки (х^* , ) можно найти следующим образом. Из первых п уравнений находим решения х^*_j( ), j = 1, …, n, как функции вектора  = (₁,…, _l)^T; подставляя далее эти решения в следующие l равенства h_i(x^*) – d_i = 0, i =1, …, l, находим значения неопределенных множителей Лагранжа _i, i =1, …, l; наконец, возвращаясь к решениям х^*_j( ), j = 1, …, n, находим их окончательное значение х^* _j, j = 1, …, n. Эти решения называются стационарными точками функции Лагранжа; для них имеет место равенство L(x^*, ) = f(x^*), что непосредственно следует из определения самой функции Лагранжа и условий h_i(x^*) – d_i = 0, i = 1, …, 1. Среди найденных стационарных решений (в общем случае все они являются локальными решениями) глобальным оптимумом является то решение, которое максимизирует или минимизирует целевую функцию f(x).

Иллюстрируем применение этого метода в решении следующей экономической задачи, известной из теории потребительского выбора [9].

Необходимо найти такой набор экономических благ (q_i,…,q_n), который удовлетворяет бюджетному ограничению и максимизирует функцию полезности, заданной в виде , где величины _j, j = 1, …, n, фиксированные параметры, p_j, j = 1, …, n, рыночные цены на единицу соответствующих благ.

С математической точки зрения мы имеем следующую задачу на максимум

(q_i,…,q_n)

Решение этой задачи находим при следующих исходных данных: п = 2; P₁=10, P₂=15; I =10000; σ₁ = 0.6, σ₂ = 0.8,функция полезности равна . На рис.2.2 иллюстрировано решение этой задачи.

уровни полезности

q₂

q₁

q₂^*

q₁^*

Бюджетная линия

Рис. 2.2. Геометрическая иллюстрация решения.

Составляем функцию Лагранжа в виде , для которой получим следующие условия теоремы Куна – Таккера

а) ,

б) ,

в) .

т.к. , из условий а) – в) получим

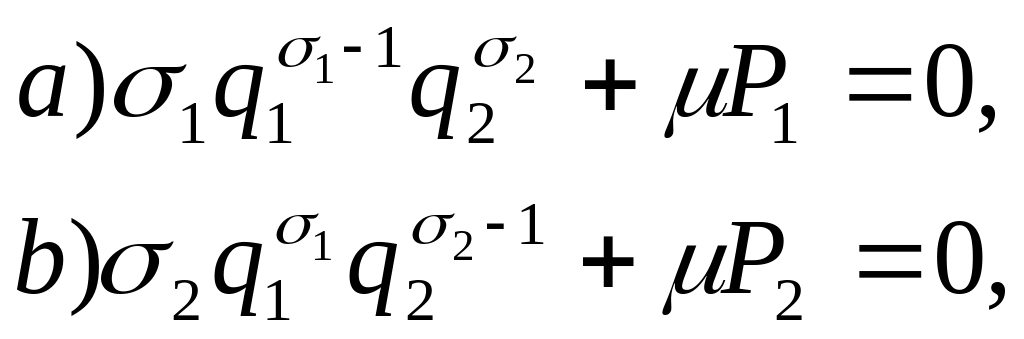
в) .

Из условий а) и б) получим выражение ₁q₂ /₂q₁ = p₁/p₂ или что эквивалентно, p₂q₂ = p₁q₁₂/₁. Тогда из уравнения бюджетной прямой следует, что p₁q₁(1 + ₂/₁) = I, откуда следует решение в виде

, ,

или в цифровом значении:

q₁^* = (10000/10)6/14 = 428.5,

q₂^* = (10000/15)8/14 = 381.

При этом общий бюджет будет распределен таким образом:

,

а отношение этих величин составляет

.