Решение.

Число всех исходов опыта равно . Число исходов, благоприятствующих событию А = {записанные номера будут идти по порядку} равно Тогда вероятность события А равна

Пример 2. 10 мячей размещают по 20 корзинам. Найти вероятности следующих событий: а) А ={в определенных 10 корзинах окажется по мячу}, б) B = {в каких-то 10 корзинах окажется по мячу}, в) C = {все 10 мячей поместятся в 3 корзины}.

Решение.

Это схема – размещение по ячейкам. Число всех исходов опыта равно .

а) В определенных 10 корзинах окажется ровно по одному мячу. Это вторая схема – размещения без возвращения, а именно перестановки (число шаров равно числу корзин). Число исходов, благоприятствующих событию А, равно Тогда вероятность события А равна

б) В каких-то 10 корзинах окажется ровно по одному мячу. Это вторая схема – размещения без возвращения. Число исходов, благоприятствующих событию В, равно . Тогда вероятность события В равна

с) Все 10 мячей поместятся в 3 корзины. Корзины не указаны, значит, мы должны выбрать три корзины из 20 (это первая схема – сочетания) и положить в них все 10 мячей, следовательно, в одной корзине может оказаться несколько мячей (это четвертая схема – размещения с повторениями). Тогда число исходов, благоприятствующих событию С, равно Вероятность события С:

Пример 3. Два раза бросается игральная кость. Найти вероятность того, что оба раза не выпадут «6»-ки?

Решение.

По замечанию в). При однократном бросании кости – 6 исходов. То есть при первом бросании – 6 исходов и при втором бросании – 6 исходов (могут оба раза выпасть одинаковые цифры). Следовательно, число всех исходов опыта равно Шестерки не выпали, значит осталось 5 вариантов на первое и второе бросание. Число исходов, благоприятствующих событию А, равно Тогда вероятность события А равна

Пп. 2. Геометрические вероятности в классической схеме

Классическая теория вероятностей основана на рассмотрении конечной группы равновероятных событий. Теория недостаточна, когда получается бесконечное множество исходов. Поэтому классическое определение несколько видоизменили для опытов с бесконечным множеством исходов, хотя при этом по-прежнему основную роль играет понятие «равновероятности» некоторых событий.

Формулировка общей задачи геометрической вероятности:

Пусть в пространстве (одномерном, двумерном, трехмерном) имеется некоторая область D и в ней содержится другая область d с квадриремой границей. В область D наудачу бросается точка. Брошенная точка может попасть в любую точку области D. Вероятность попасть при бросании в какую-либо часть области D пропорциональна мере (mes) этой части (длине, площади, объему в зависимости от рассматриваемого пространства) и не зависит от ее расположения и формы. Вероятность попадания в область d при бросании наудачу точки в область D находится по формуле:

формула геометрической вероятности.

Частные случаи.

1. Пусть отрезок l составляет часть отрезка L. Вероятность попадания на отрезок l при бросании наудачу точки на отрезок L находится по формуле .

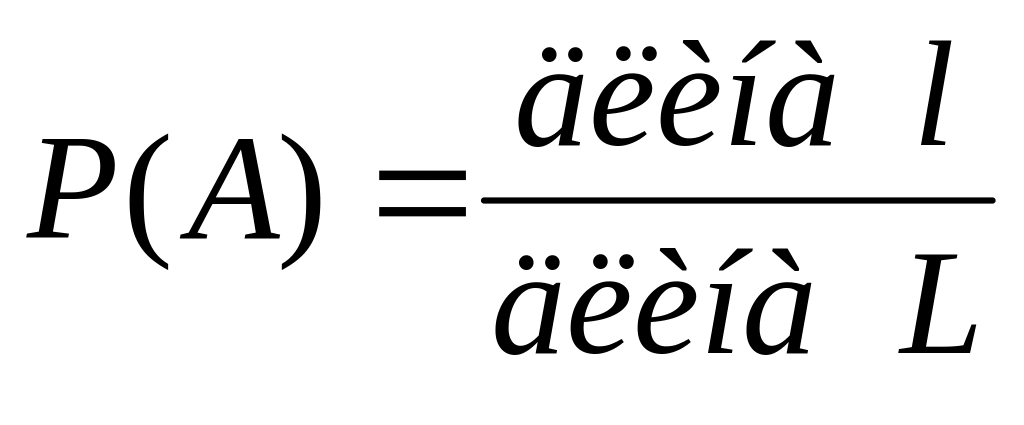2. Пусть плоская фигура s составляет часть плоской фигуры S. Вероятность попадания на фигуру s при бросании наудачу точки в область S находится по формуле .

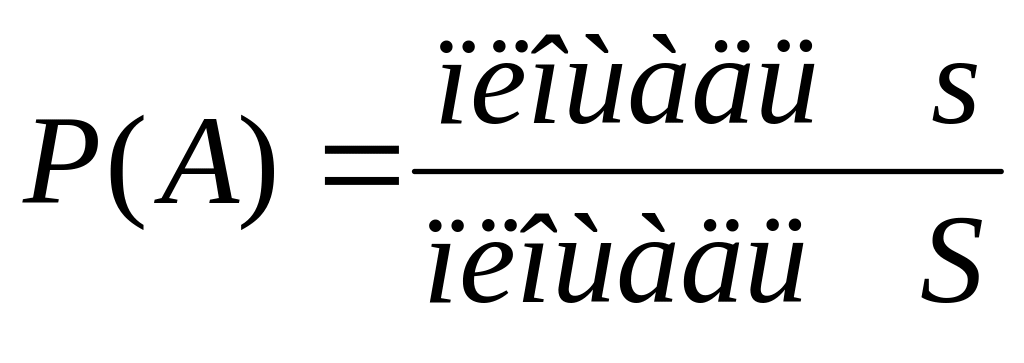3. Пусть объемная фигура v составляет часть объемной фигуры V. Вероятность попадания в фигуру v при бросании наудачу точки в область V находится по формуле .

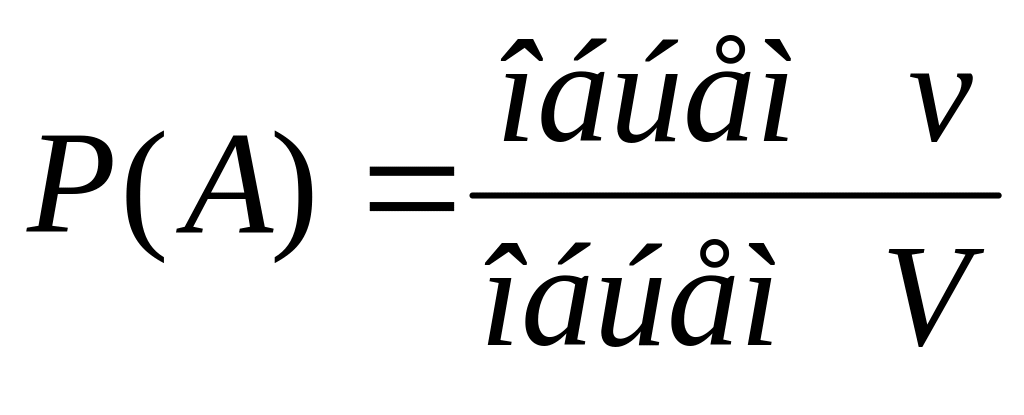Пример 1 (задача о встрече). Два лица А и В условились встретиться в определенном месте между 12 часами и часом. Пришедший первым ждет другого в течение 20 минут, после чего уходит. Чему равна вероятность встречи лиц А и В, если приход каждого из них в течение указанного часа может произойти наудачу, и моменты прихода независимы.

Решение.

Обозначим моменты прихода лица А через х, а лица В через у, причем .

Для того, чтобы встреча произошла, необходимо и достаточно, чтобы х и у удовлетворяли неравенству или, что то же самое, (это неравенство означает: пришедший первым ждет другого в течение 20 минут).

Раскроем модуль: .

И

у

зобразим х и у как декартовые координаты на плоскости. За единицу масштаба примем минуту. Всевозможные исходы – точки квадрата со сторонами 60. Благоприятствующие встрече исходы – точки области между прямыми и .

60

у=х+20

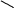
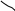
Вероятность встречи лиц А и В равна отношению площади заштрихованной

у=х-20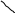

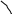
фигуры к площади всего квадрата:

х

О

60

20

20

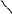
Пример 2 (Задача Бюффона).

Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2а. На плоскость наудачу бросается игла длины 2l (l < a), то есть 1) центр иглы наудачу падает на отрезок длины 2а, перпендикулярный к проведенным прямым, 2) вероятность того, что угол φ, составленный иглой и проведенными прямыми, будет заключаться между φ₁ и φ₁+Δφ, пропорциональна Δφ, 3) величины х и φ независимы. Найти вероятность того, что игла пересечет какую-нибудь прямую.