Доказательство.
Действительно, для ДСВ в сумме
при симметричном относительно mX
законе распределения и нечетном s
каждому положительному слагаемому
соответствует равное ему по абсолютной
величине отрицательное слагаемое так,
что вся сумма равна 0. Аналогично. Для
НСВ
как интеграл в симметричных пределах
от нечетной функции.
(что и требовалось доказать).
В связи с этим, в качестве характеристики асимметрии и выбирают простейший нечетный момент – третий . Он имеет размерность куба СВ, для получения безразмерной характеристики рассматривают отношение к среднему квадратическому в третьей степени:
Определение 48. Коэффициентом
асимметрии Sk
случайной величины Х называется
величина
.
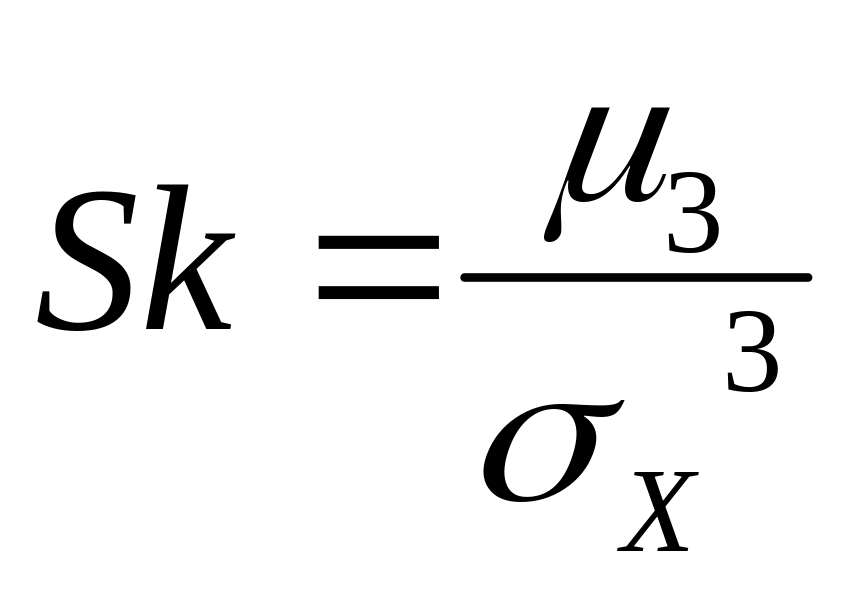(12)
.
связь между начальными и центральным
моментом 3-го порядка.
И эксцесс
Четвертый центральный момент служит для характеристики «крутости», т. е. островершинности или плосковершинности распределения.
Это свойство описывается с помощью эксцесса.
Определение 49. Эксцессом
случайной величины Х называется величина
.
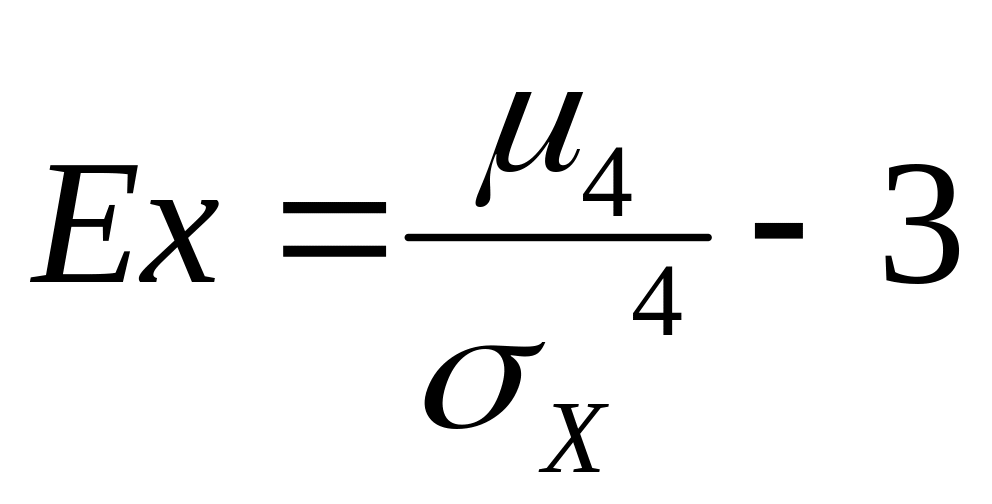(13)
Число 3 вычитается из соотношения
потому, что для наиболее распространенного
нормального закона распределения НСВ
(с которым познакомимся позднее)
.
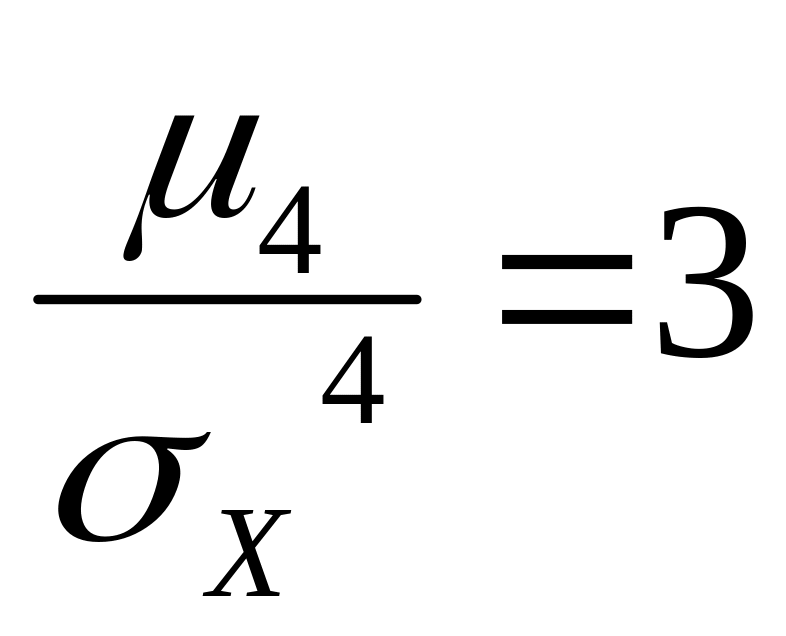Кривая нормального распределения, для которого эксцесс равен нулю, принята как бы за эталон, с которым сравниваются другие распределения. Кривые более островершинные имеют положительный эксцесс, более плосковершинные – отрицательный.
Абсолютные моменты
– начальный абсолютный момент.
– центральный абсолютный момент.
Абсолютные моменты четных порядков совпадают с обычными моментами. Из абсолютных моментов нечетного порядка чаще всего применяется первый абсолютный центральный момент:
– среднее арифметическое отклонение.
а) Для дискретных случайных
величин:
,
(14)
b) Для
непрерывных случайных величин:
(15)
применяется как характеристика
рассеивания (как и DX
и
).
Замечания.
1. Моменты могут рассматриваться
не только относительно начала координат
(начальные) или математического ожидания
(центральные), но и относительно
произвольной точки а:
.
2. Во многих задачах полная характеристика случайной величины (закон распределения) не нужна или не может быть получена, поэтому ограничиваются приблизительным описанием СВ с помощью числовых характеристик, каждая из которых выражает какое-либо характерное свойство распределения. Иногда характеристиками пользуются для приближенной замены одного распределения другим.
Пример 1. Дан ряд распределения ДСВ:
xi |
–1 |
0 |
1 |
pi |
0,4 |
0,2 |
a |
Найти: 1) величину а, 2) математическое
ожидание и дисперсию
и D[X]
, 3)
,
.