П. 3. Плотность распределения вероятностей нсв

Пусть Х – непрерывная случайная величина, ее функция распределения F(x) – непрерывная и дифференцируемая функция. Рассмотрим участок [x; x+∆x), где ∆x – длина участка. Тогда вероятность попадания СВ Х на данный участок можно найти по формуле (по свойству 6):

Рассмотрим предел отношения приращения функции F(x) на участке к длине этого участка (или среднюю вероятность, приходящуюся на единицу длины участка) при условии, что длина стягивается в точку:

– по определению производной.

Определение 36. Предел отношения вероятности попадания НСВ на элементарный участок от х до x + ∆x к длине этого участка, когда ∆x стремится к нулю или производная функции распределения НСВ называется плотностью распределения НСВ Х в точке х и обозначается f(x):

= f(x).

Другие названия плотности: плотность вероятности, дифференциальная функция распределения, дифференциальный закон распределения.

f(x) существует только для непрерывных СВ. Она является одной из форм закона распределения.

f(x) характеризует плотность, с которой распределяются значения СВ в данной точке.

Механическая интерпретация: f(x) характеризует плотность распределения масс по оси абсцисс.

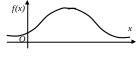
Определение 37. Кривая, изображающая плотность распределения f(x) СВ, называется кривой распределения.

Замечание. Если возможные значения СВ заполняют некоторый конечный промежуток, то f(x) = 0 вне этого промежутка.

Геометрическая интерпретация f(x) .

Перепишем определение: .

И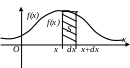 з данного равенства следует, что , причем, т. к. х – независимая переменная, то ∆x = dx.

Отсюда следует, что ,

где S – площадь элементарного прямоугольника, опирающегося на участок dx. (см. рис.)

При dx площадь прямоугольника приближается к площади криволинейной трапеции, которую можно найти с помощью определенного интеграла: .

Величина f(x)dx называется элементом вероятности.

Рассмотрим большой участок (α; β) , тогда:

. (1)

Вероятность того, что НСВ примет значение, принадлежащее интервалу (α; β), равна площади криволинейной трапеции, опирающейся на интервал (α; β) оси (Ох) :

Замечание. Для НСВ непринципиально, какие знаки в неравенстве брать < или : , т. е. включать или не включать крайние точки интервала, потому что в них вероятность все равно равна нулю.