
- •Теория вероятностей
- •§ 1. Предмет теории вероятностей
- •§ 2. Случайные события или исходы. Множество элементарных событий. Основные понятия
- •Примеры на построение множества ω.
- •Алгебраические операции над событиями
- •Диаграмма Венна.
- •Свойства операций
- •§ 3. Различные подходы к определению вероятности
- •П. 1. Аксиоматическое определение вероятности
- •П. 2. Классическое определение вероятности
- •Решение.
- •Решение.
- •Пп. 1. Комбинаторный метод вычисления вероятностей в классической схеме
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Пп. 2. Геометрические вероятности в классической схеме
- •Решение.
- •П. 3. Статистическое определение вероятности
- •§ 4. Основные теоремы теории вероятностей п.1. Теоремы сложения вероятностей
- •Доказательство.
- •Доказательство (методом математической индукции).
- •Доказательство.
- •Доказательство.
- •Решение.
- •Д оказательство (геометрическое)
- •П.2. Теоремы умножения вероятностей
- •Доказательство.
- •Решение.
- •Решение.
- •§ 5. Формулы полной вероятности и формула Байеса п. 1. Формула полной вероятности (следствие обеих основных теорем сложения и умножения)
- •Решение.
- •П. 2. Формула Байеса (Бейеса) (следствие теоремы умножения и формулы полной вероятности)
- •Решение.
- •§ 6. Последовательность независимых испытаний п. 1. Независимые испытания
- •П. 2. Формулы Бернулли.
- •Решение.
- •Решение.
- •Замечания.
- •Решение.
- •П. 3. Предельные теоремы в схеме Бернулли
- •Решение.
- •Решение.
- •Доказательство.
- •Решение.
- •П. 4. Наивероятнейшее число появления события в независимых испытаниях
- •Решение.
- •§ 7. Случайные величины п. 1. Основные определения
- •П. 2. Законы распределения случайных величин. Законы распределения дискретных случайных величин. Функция распределения
- •Формы закона распределения дсв.
- •Решение.
- •Решение.
- •3. Функция распределения – универсальный закон распределения (для дсв и нсв).
- •Свойства f(X).
- •Доказательство.
- •Графики функции распределения.
- •Решение.
- •Решение.
- •П. 3. Плотность распределения вероятностей нсв
- •Свойства плотности распределения
- •2. Условие нормировки: интеграл в бесконечных пределах от плотности распределения равен 1: . (4) Доказательство
- •Решение.
- •Решение.
- •П. 4. Числовые характеристики случайных величин, их роль и назначение
- •Пп 1. Характеристики положения (математическое ожидание, мода, медиана)
- •1. Математическое ожидание или среднее значение случайной величины
- •2. Мода случайной величины
- •3. Медиана случайной величины
- •Пп 2. Моменты
- •Доказательство.
- •И эксцесс
- •Решение.
- •Решение.
- •Решение.
- •П. 5. Законы распределения вероятностей дискретных случайных величин: биномиальный, Пуассона, гипергеометрический. Пп 1. Биномиальное распределение
- •Решение.
- •Пп 2. Распределение Пуассона
- •Решение.
- •Решение.
- •Пп 3. Гипергеометрическое распределение
- •Решение.
- •П. 6. Законы распределения вероятностей непрерывных случайных величин: равномерный, показательный, нормальный Пп 1. Равномерное распределение или закон равномерной плотности
- •Решение.
- •Пп 2. Показательное или экспоненциальное распределение
- •Решение.
- •Пп 3. Нормальный закон распределения
- •Смысл параметров m и σ
- •Решение.
- •§ 8. Системы случайных величин или случайные векторы п. 1. Основные понятия.
- •П. 2. Законы распределения свдт и свнт
- •Закон. Таблица распределения – закон распределения свдт.
- •Решение.
- •Решение.
- •Закон. Функция распределения – закон распределения свдт и свнт.
- •Решение.
- •3. Плотность распределения (для свнт)
- •Решение.
- •Решение.
- •П. 4. Плотности распределения отдельных величин, входящих в систему. Равномерное и нормальное распределения. Условные законы распределения
- •Решение.
- •Решение.
- •П. 5. Числовые характеристики системы. Корреляция. Линии регрессии
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •§ 9. Закон больших чисел. Предельные теоремы теории вероятностей
Решение.
xi \ yj |
0 |
1 |
2 |
0 |
0 |
0 |
|
1 |
0 |
|
0 |
2 |
|
0 |
0 |
Случайный вектор дискретного типа, следовательно, F(x,y) = .
F(x, y) |
y ≤ 0 |
0 < y ≤ 1 |
1 < y ≤ 2 |
y > 2 |
x ≤ 0 |
0 |
0 |
0 |
0 |
0 < x ≤ 1 |
0 |
0 |
0 |
|
1 < x ≤ 2 |
0 |
0 |
|
+ |
x > 2 |
0 |
|
+ |
+ + =1 |
Пояснение:
![]() .
.
![]() =
=
![]() .
.
![]() =
=![]()
![]()
![]()
![]() .
.
![]() .
.
Ковариация, корреляция. Линии регрессии
Особую роль при исследовании системы играет второй смешанный центральный момент.
Определение 72. Второй смешанный центральный момент μ11 называется корреляционным или моментом связи или ковариацией:
![]() .
.
![]()
![]() для СВДТ .
для СВДТ .
![]() для СВНТ.
для СВНТ.
Теория корреляции решает две задачи: 1) установление формы связи между случайными величинами, 2) определение тесноты и силы этой связи.
![]() , помимо рассеивания, характеризует
взаимное влияние случайных величин
X и Y,
входящих в систему. Для оценки степени
влияния используется не сам момент, а
безразмерное соотношение, которое
называется нормированной ковариацией
или коэффициентом корреляции:
, помимо рассеивания, характеризует
взаимное влияние случайных величин
X и Y,
входящих в систему. Для оценки степени
влияния используется не сам момент, а
безразмерное соотношение, которое
называется нормированной ковариацией
или коэффициентом корреляции:
![]() –
–
коэффициент корреляции двух случайных компонент X и Y случайного вектора.
(Иногда его обозначают как
![]() ).
).
Средние квадратические отклонения
случайных величин Х и У равны
![]() ,
,
![]() .
.
Определение 17. X
и Y называются
некоррелированными случайными величинами,
если их коэффициент корреляции
![]() ,
и коррелированными, если отличен от
нуля.
,
и коррелированными, если отличен от
нуля.
Свойства коэффициента корреляции
![]() :
:
Если X и Y – независимые СВ, то =
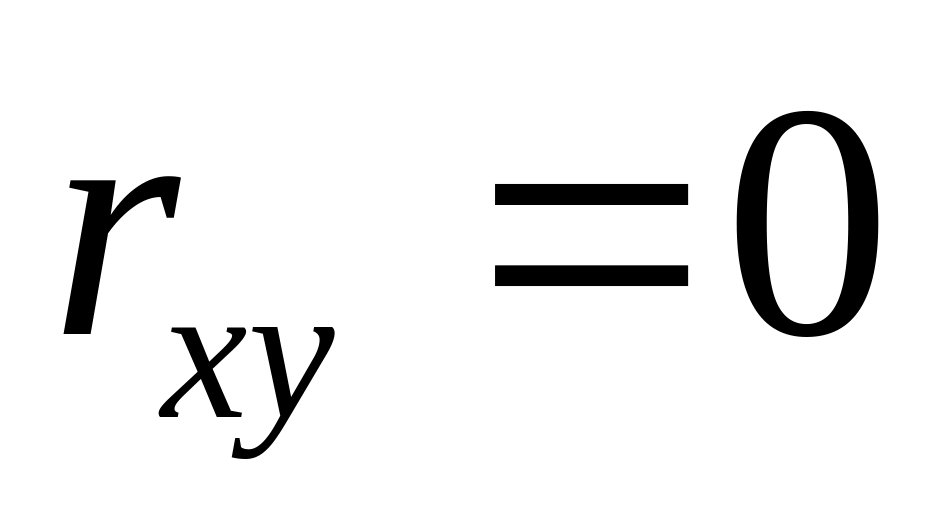 .
(X и Y
некоррелированные случайные величины).
Обратное утверждение неверно, так как
X и Y
могут быть зависимыми, но при этом
.
.
(X и Y
некоррелированные случайные величины).
Обратное утверждение неверно, так как
X и Y
могут быть зависимыми, но при этом
.
 .
.В случае
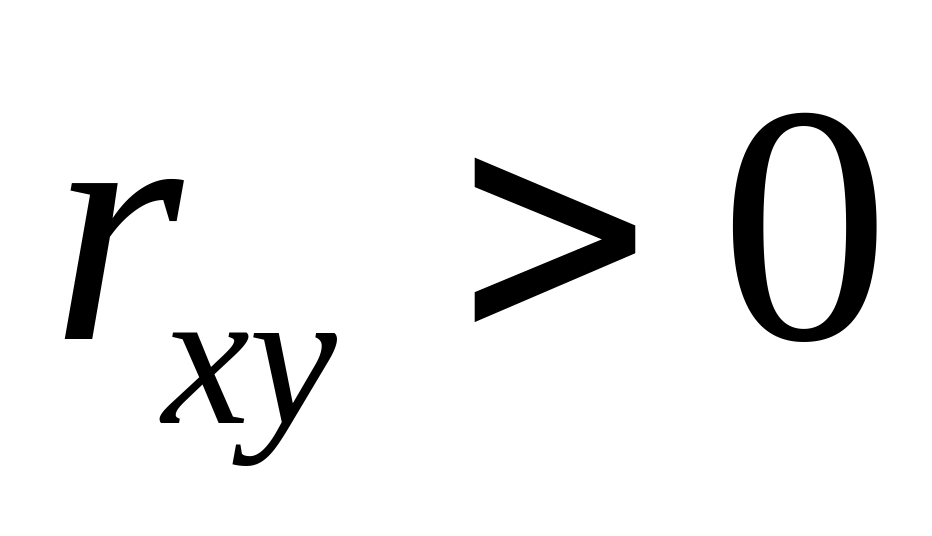 говорят о положительной корреляции Х
и Y , что означает: при
возрастании одной из них
другая тоже имеет тенденцию в среднем
возрастать. Например, вес и рост человека.
говорят о положительной корреляции Х
и Y , что означает: при
возрастании одной из них
другая тоже имеет тенденцию в среднем
возрастать. Например, вес и рост человека.В случае
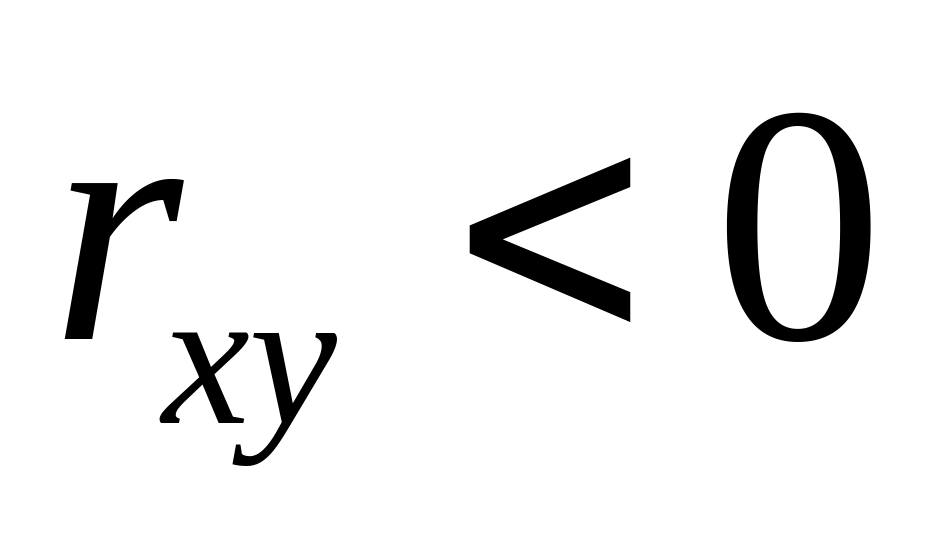 говорят об отрицательной корреляции
Х и Y , что означает:
при возрастании одной из них другая
имеет тенденцию в среднем убывать.
Например, время, потраченное на подготовку
прибора к работе и количество
неисправностей, обнаруженных при его
работе.
говорят об отрицательной корреляции
Х и Y , что означает:
при возрастании одной из них другая
имеет тенденцию в среднем убывать.
Например, время, потраченное на подготовку
прибора к работе и количество
неисправностей, обнаруженных при его
работе.
Взаимная связь двух случайных величин,
помимо
,
может быть описана с помощью линий
регрессии. Действительно, хотя при
каждом значении Х = x
величина Y остается
случайной величиной, допускающей
рассеивание своих значений, однако
зависимость Y от Х
сказывается часто в изменении средних
размеров Y при переходе
от одного значения х к другому. С
изменением х будет изменяться и
![]() .
Это означает, что можно рассматривать
функцию
.
Это означает, что можно рассматривать
функцию
![]() =
,
областью определения которой является
множество возможных значений случайной
величины Х. Эта функция носит
название регрессии Y
по Х.
=
,
областью определения которой является
множество возможных значений случайной
величины Х. Эта функция носит
название регрессии Y
по Х.
Аналогично, зависимость X
от Y описывает функция
![]() =
=
![]() .
.
![]() и
и
![]() – уравнения регрессии
– уравнения регрессии
Линии, определенные этими уравнениями, называются кривыми или линиями регрессии. (Вводятся лишь для непрерывных СВ, для ДСВ линии будут состоять из точек.)
Если обе линии регрессии – прямые, то корреляционную зависимость называют линейной (линейная корреляция). Для нормально распределенного случайного вектора (X,Y) уравнения регрессии линейные:
![]() ,
,
![]() .
.
Связь коэффициента корреляции и линий регрессии
1) Если
![]() ,
то линии регрессии наклонены вправо.
,
то линии регрессии наклонены вправо.
2) Если
![]() ,
то линии регрессии наклонены влево.
,
то линии регрессии наклонены влево.
3) Если , то линии регрессии проходят параллельно осям координат.
4) Если,
![]() ,
то линии регрессии сливаются в одну
линию, а случайные величины X
и Y связаны между собой
линейной функциональной зависимостью
,
то линии регрессии сливаются в одну
линию, а случайные величины X
и Y связаны между собой
линейной функциональной зависимостью
![]() ,
,
![]() ,
причем знак коэффициента корреляции
(+ rХУ ) или
(– rХУ)
берется в зависимости от знака (+ или –)
коэффициента а, который называется
коэффициентом регрессии.
,
причем знак коэффициента корреляции
(+ rХУ ) или
(– rХУ)
берется в зависимости от знака (+ или –)
коэффициента а, который называется
коэффициентом регрессии.
Часто пишут уравнение в виде:
![]() и
называют его уравнением парной
регрессии, где коэффициент регрессии
и
называют его уравнением парной
регрессии, где коэффициент регрессии
![]() .
.
Определение 73. Ковариационной
матрицей случайного вектора называется
симметрическая действительная матрица,
элемент которой представляет собой
ковариации соответствующих пар
компонент:![]()
![]() .
.
Определение 74. Корреляционной
матрицей случайного вектора называется
нормированная ковариационная матрица![]() .
.
Пример 9. Дано уравнение парной
регрессии
![]() .
Выберите правильный коэффициент
корреляции: 1)
= 0,6, 2)
= – 0,6, 3)
=1,2.
.
Выберите правильный коэффициент
корреляции: 1)
= 0,6, 2)
= – 0,6, 3)
=1,2.
