
- •Теория вероятностей
- •§ 1. Предмет теории вероятностей
- •§ 2. Случайные события или исходы. Множество элементарных событий. Основные понятия
- •Примеры на построение множества ω.
- •Алгебраические операции над событиями
- •Диаграмма Венна.
- •Свойства операций
- •§ 3. Различные подходы к определению вероятности
- •П. 1. Аксиоматическое определение вероятности
- •П. 2. Классическое определение вероятности
- •Решение.
- •Решение.
- •Пп. 1. Комбинаторный метод вычисления вероятностей в классической схеме
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Пп. 2. Геометрические вероятности в классической схеме
- •Решение.
- •П. 3. Статистическое определение вероятности
- •§ 4. Основные теоремы теории вероятностей п.1. Теоремы сложения вероятностей
- •Доказательство.
- •Доказательство (методом математической индукции).
- •Доказательство.
- •Доказательство.
- •Решение.
- •Д оказательство (геометрическое)
- •П.2. Теоремы умножения вероятностей
- •Доказательство.
- •Решение.
- •Решение.
- •§ 5. Формулы полной вероятности и формула Байеса п. 1. Формула полной вероятности (следствие обеих основных теорем сложения и умножения)
- •Решение.
- •П. 2. Формула Байеса (Бейеса) (следствие теоремы умножения и формулы полной вероятности)
- •Решение.
- •§ 6. Последовательность независимых испытаний п. 1. Независимые испытания
- •П. 2. Формулы Бернулли.
- •Решение.
- •Решение.
- •Замечания.
- •Решение.
- •П. 3. Предельные теоремы в схеме Бернулли
- •Решение.
- •Решение.
- •Доказательство.
- •Решение.
- •П. 4. Наивероятнейшее число появления события в независимых испытаниях
- •Решение.
- •§ 7. Случайные величины п. 1. Основные определения
- •П. 2. Законы распределения случайных величин. Законы распределения дискретных случайных величин. Функция распределения
- •Формы закона распределения дсв.
- •Решение.
- •Решение.
- •3. Функция распределения – универсальный закон распределения (для дсв и нсв).
- •Свойства f(X).
- •Доказательство.
- •Графики функции распределения.
- •Решение.
- •Решение.
- •П. 3. Плотность распределения вероятностей нсв
- •Свойства плотности распределения
- •2. Условие нормировки: интеграл в бесконечных пределах от плотности распределения равен 1: . (4) Доказательство
- •Решение.
- •Решение.
- •П. 4. Числовые характеристики случайных величин, их роль и назначение
- •Пп 1. Характеристики положения (математическое ожидание, мода, медиана)
- •1. Математическое ожидание или среднее значение случайной величины
- •2. Мода случайной величины
- •3. Медиана случайной величины
- •Пп 2. Моменты
- •Доказательство.
- •И эксцесс
- •Решение.
- •Решение.
- •Решение.
- •П. 5. Законы распределения вероятностей дискретных случайных величин: биномиальный, Пуассона, гипергеометрический. Пп 1. Биномиальное распределение
- •Решение.
- •Пп 2. Распределение Пуассона
- •Решение.
- •Решение.
- •Пп 3. Гипергеометрическое распределение
- •Решение.
- •П. 6. Законы распределения вероятностей непрерывных случайных величин: равномерный, показательный, нормальный Пп 1. Равномерное распределение или закон равномерной плотности
- •Решение.
- •Пп 2. Показательное или экспоненциальное распределение
- •Решение.
- •Пп 3. Нормальный закон распределения
- •Смысл параметров m и σ
- •Решение.
- •§ 8. Системы случайных величин или случайные векторы п. 1. Основные понятия.
- •П. 2. Законы распределения свдт и свнт
- •Закон. Таблица распределения – закон распределения свдт.
- •Решение.
- •Решение.
- •Закон. Функция распределения – закон распределения свдт и свнт.
- •Решение.
- •3. Плотность распределения (для свнт)
- •Решение.
- •Решение.
- •П. 4. Плотности распределения отдельных величин, входящих в систему. Равномерное и нормальное распределения. Условные законы распределения
- •Решение.
- •Решение.
- •П. 5. Числовые характеристики системы. Корреляция. Линии регрессии
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •§ 9. Закон больших чисел. Предельные теоремы теории вероятностей
Решение.
По условию
![]() ,
тогда
,
тогда
![]() ,
так как
,
так как
![]() .
.
![]() .
.
Пп 3. Нормальный закон распределения
Определение 56. НСВ Х распределена по нормальному закону, если ее плотность распределения f(x) имеет вид:
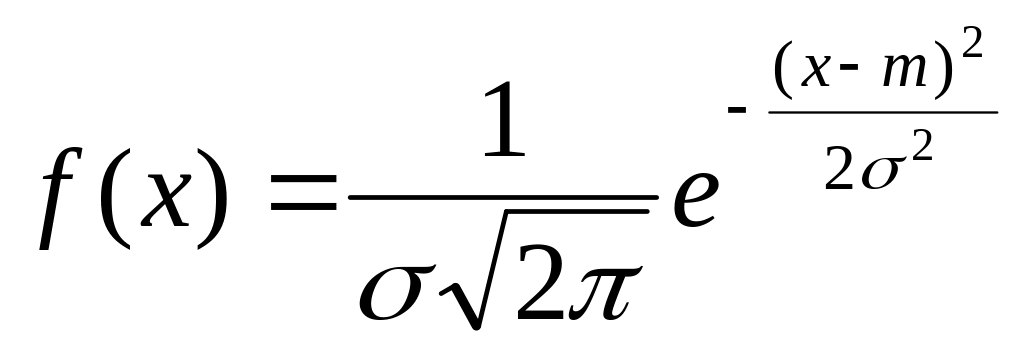 ,
где
,
где
![]() .
.
Нормальный закон называют еще законом распределения Гаусса.
Говорят, что случайная величина Х подчинена нормальному закону и пишут N(m, σ).
Примеры типовых задач: случайные величины в них характеризуют ошибки при измерениях, боковые отклонения и отклонения по дальности при стрельбе, величина износа деталей…
График плотности или кривая распределения
называется гауссовской кривой.
Она имеет симметричный холмообразный
вид. При x = m
![]() .
Ветви кривой быстро приближаются к оси
(Ох): площадь под кривой на участке
.
Ветви кривой быстро приближаются к оси
(Ох): площадь под кривой на участке
![]() равна 90% площади под всей кривой.
равна 90% площади под всей кривой.
Г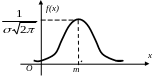 лавная
особенность нормального закона
состоит в том, что он является предельным
законом, к которому приближаются другие
законы распределения при весьма часто
встречающихся типичных условиях.
лавная
особенность нормального закона
состоит в том, что он является предельным
законом, к которому приближаются другие
законы распределения при весьма часто
встречающихся типичных условиях.
Кривые распределения по всем другим законам распределения получаются из одной единственной кривой – гауссовской.
Для наглядной демонстрации нормального закона распределения иногда используют специальное устройство – доску Гальтона. В нем падающие сверху шарики распределяются между правильными шестиугольниками и в результате падают на горизонтальную поверхность, образуя картинку, похожую на подграфик гауссовой кривой.
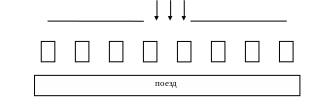
Распределение пассажиров по вагонам метро – гауссово распределение. Покажем это. Пассажиры метро бегут по переходу, выходящему на середину станции, на поезд, стоящий напротив выхода из перехода. Платформа, у которой стоит поезд, равномерно разделена колоннами. Ясно, что большинство пассажиров войдет в средние вагоны, а по мере удаления вагонов от центра, количество садящихся в них людей будет уменьшаться.
Замечание. С гауссовской плотностью f(x) мы встречались при рассмотрении локальной теоремы Муавра- Лапласа.
1. Убедимся, что f(x)
действительно плотность НСВ, для чего
проверим равенство
(условие нормировки). Известно, что
![]() (интеграл Пуассона).
(интеграл Пуассона).
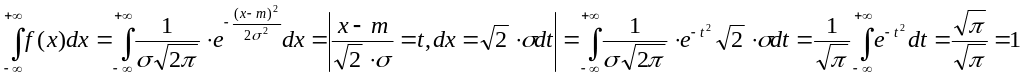 Что
и требовалось доказать.
Что
и требовалось доказать.
2. Докажем, что численные параметры m
и σ совпадают с основными
характеристиками распределения:
![]() – мат. ожидание,
– мат. ожидание,
![]() –
среднеквадратическое отклонение. Для
этого вычислим
–
среднеквадратическое отклонение. Для
этого вычислим
![]() и
.
и
.
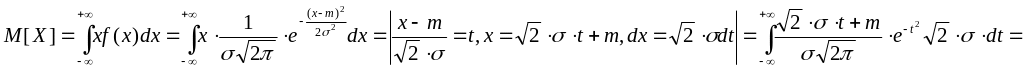
![]() .
.
Таким образом, . Этот параметр, особенно в задачах стрельбы, называют центром рассеивания.
Доказать самостоятельно, что . (Сначала вычислить дисперсию).
Смысл параметров m и σ
.
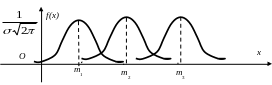
m – центр симметрии распределения (т.к. при изменении знака разности (x – m) в формуле плотности на противоположный, выражение не меняется). Если изменять центр рассеивания m, то кривая распределения будет смещаться вдоль оси (Ох), не изменяя своей формы. Следовательно, m характеризует положение распределения на оси (Ох).
Размерность m та же, что и размерность случайной величины Х.
В задачах m означает систематические ошибки.
σ характеризует форму кривой распределения, т.к. это характеристика рассеивания. Площадь под кривой распределения всегда должна быть равна 1. Наибольшая ордината кривой распределения обратно пропорциональна σ, следовательно, при увеличении σ максимальная ордината уменьшается.
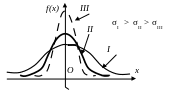
Размерность σ совпадает с размерностью СВ.
В задачах σ означает стандартные ошибки.
Замечания.
1. В некоторых курсах теории
вероятностей вводят понятие меры
точности
![]() ,
тогда нормальный закон запишется в
виде:
,
тогда нормальный закон запишется в
виде:
![]()
2.
![]()
![]() .
.
3. Если НСВ Х распределяется по закону N(0, 1), то она называется стандартизованной случайной величиной.
Формула для центральных моментов любого порядка имеет вид:
![]() .
.
Т.к.
![]() ,
то все нечетные моменты равны 0 (это
следует из симметричности нормального
закона).
,
то все нечетные моменты равны 0 (это
следует из симметричности нормального
закона).
Для четных моментов:
![]() ,
т.е.
,
т.е.
![]()
![]()
![]()
Асимметрия нормального закона
![]() эксцесс
эксцесс
![]() (назначение эксцесса характеризовать
крутость законов по сравнению с нормальным
законом), мода
(назначение эксцесса характеризовать
крутость законов по сравнению с нормальным
законом), мода
![]() медиана
медиана
![]()
Найдем вероятность попадания НСВ Х, подчиненной нормальному закону с параметрами m и σ, на участок от α до β.
![]() или
или
![]() ,
тогда
,
тогда

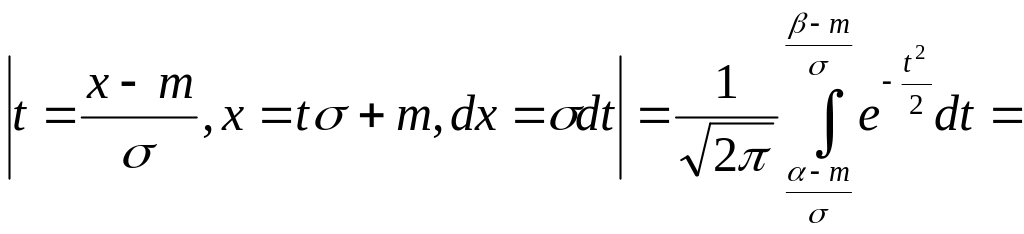 (интеграл вычисляется с помощью
специальной функции – функции Лапласа
Ф(х) [смотри предельную интегральную
теорему Муавра-Лапласа §6 п. 3])
(интеграл вычисляется с помощью
специальной функции – функции Лапласа
Ф(х) [смотри предельную интегральную
теорему Муавра-Лапласа §6 п. 3])
=
![]()
![]() .
.
Итак, .
Вероятность попадания НСВ Х
левее β находится по
формуле:
![]()
![]() .
.
Свойства функции Лапласа
Ф(x) определена для всех действительных х.
Ф(–∞) = 0.
Ф(x) неубывающая, т. е. возрастает на R.
Ф(–x) = 1 – Ф(x) (это следует из симметричности нормального распределения с параметрами m = 0, σ =1 относительно начала координат).
Ф(+∞) =

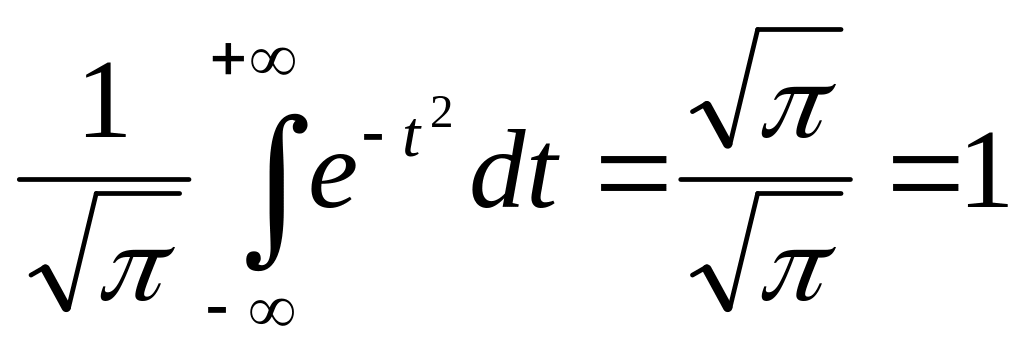 .
.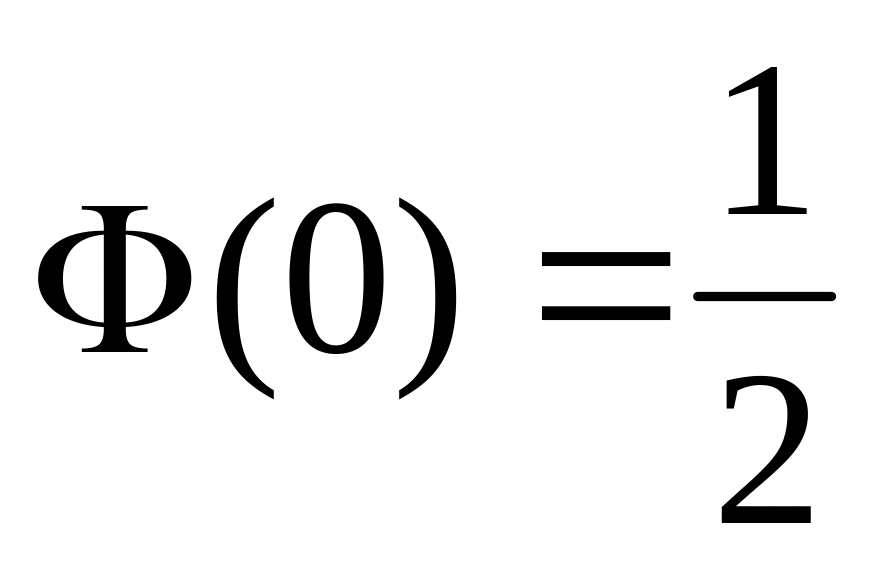 ,
,
7.
![]()
![]() – формула для нахождения вероятности
того, что абсолютная величина отклонения
СВ Х от числа m
меньше положительного числа δ, где δ –
ошибка.
– формула для нахождения вероятности
того, что абсолютная величина отклонения
СВ Х от числа m
меньше положительного числа δ, где δ –
ошибка.
Если m = 0, то
![]() .
.
Вывод 7 свойства.
Из 4 свойства и формулы для вычисления интервальных вероятностей имеем, что:
![]()
![]()
![]()
=
![]()
![]() 1+
1+![]()
![]()
Функция Лапласа затабулирована. Для тех значений x, которых нет в таблице: , Ф(x) = 1.
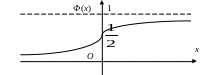
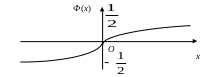
Свойства функции Лапласа
Ф(x) определена для всех действительных х.
Ф(0) = 0.
Ф(x) неубывающая, т. е. возрастает на R.
Ф(–x) = – Ф(x).
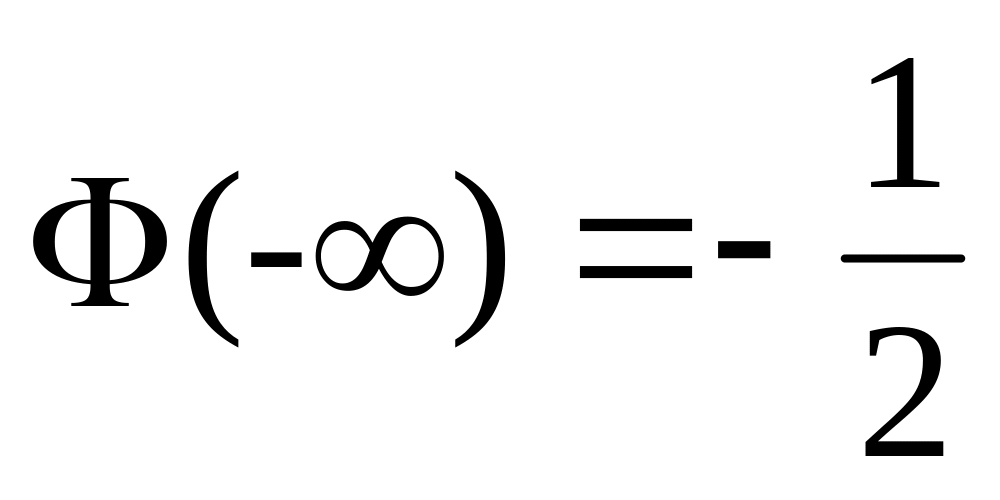 .
.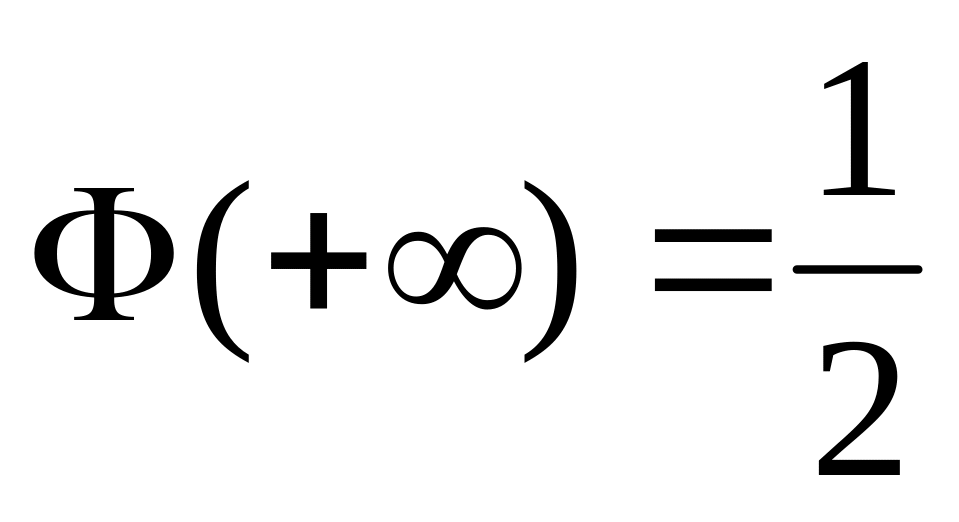 .
.
7.
![]() .
Если m = 0, то
.
.
Если m = 0, то
.
Функция Лапласа затабулирована. Для
тех значений x, которых
нет в таблице:
,
![]() .
.
Пример. Длина изготовленной
автоматом детали представляет собой
случайную величину, распределенную по
нормальному закону с параметрами m
= 10, σ =
![]() .
Найти вероятность брака, если допустимые
размеры детали 10 ± 0,05.
.
Найти вероятность брака, если допустимые
размеры детали 10 ± 0,05.
