
- •Теория вероятностей
- •§ 1. Предмет теории вероятностей
- •§ 2. Случайные события или исходы. Множество элементарных событий. Основные понятия
- •Примеры на построение множества ω.
- •Алгебраические операции над событиями
- •Диаграмма Венна.
- •Свойства операций
- •§ 3. Различные подходы к определению вероятности
- •П. 1. Аксиоматическое определение вероятности
- •П. 2. Классическое определение вероятности
- •Решение.
- •Решение.
- •Пп. 1. Комбинаторный метод вычисления вероятностей в классической схеме
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Пп. 2. Геометрические вероятности в классической схеме
- •Решение.
- •П. 3. Статистическое определение вероятности
- •§ 4. Основные теоремы теории вероятностей п.1. Теоремы сложения вероятностей
- •Доказательство.
- •Доказательство (методом математической индукции).
- •Доказательство.
- •Доказательство.
- •Решение.
- •Д оказательство (геометрическое)
- •П.2. Теоремы умножения вероятностей
- •Доказательство.
- •Решение.
- •Решение.
- •§ 5. Формулы полной вероятности и формула Байеса п. 1. Формула полной вероятности (следствие обеих основных теорем сложения и умножения)
- •Решение.
- •П. 2. Формула Байеса (Бейеса) (следствие теоремы умножения и формулы полной вероятности)
- •Решение.
- •§ 6. Последовательность независимых испытаний п. 1. Независимые испытания
- •П. 2. Формулы Бернулли.
- •Решение.
- •Решение.
- •Замечания.
- •Решение.
- •П. 3. Предельные теоремы в схеме Бернулли
- •Решение.
- •Решение.
- •Доказательство.
- •Решение.
- •П. 4. Наивероятнейшее число появления события в независимых испытаниях
- •Решение.
- •§ 7. Случайные величины п. 1. Основные определения
- •П. 2. Законы распределения случайных величин. Законы распределения дискретных случайных величин. Функция распределения
- •Формы закона распределения дсв.
- •Решение.
- •Решение.
- •3. Функция распределения – универсальный закон распределения (для дсв и нсв).
- •Свойства f(X).
- •Доказательство.
- •Графики функции распределения.
- •Решение.
- •Решение.
- •П. 3. Плотность распределения вероятностей нсв
- •Свойства плотности распределения
- •2. Условие нормировки: интеграл в бесконечных пределах от плотности распределения равен 1: . (4) Доказательство
- •Решение.
- •Решение.
- •П. 4. Числовые характеристики случайных величин, их роль и назначение
- •Пп 1. Характеристики положения (математическое ожидание, мода, медиана)
- •1. Математическое ожидание или среднее значение случайной величины
- •2. Мода случайной величины
- •3. Медиана случайной величины
- •Пп 2. Моменты
- •Доказательство.
- •И эксцесс
- •Решение.
- •Решение.
- •Решение.
- •П. 5. Законы распределения вероятностей дискретных случайных величин: биномиальный, Пуассона, гипергеометрический. Пп 1. Биномиальное распределение
- •Решение.
- •Пп 2. Распределение Пуассона
- •Решение.
- •Решение.
- •Пп 3. Гипергеометрическое распределение
- •Решение.
- •П. 6. Законы распределения вероятностей непрерывных случайных величин: равномерный, показательный, нормальный Пп 1. Равномерное распределение или закон равномерной плотности
- •Решение.
- •Пп 2. Показательное или экспоненциальное распределение
- •Решение.
- •Пп 3. Нормальный закон распределения
- •Смысл параметров m и σ
- •Решение.
- •§ 8. Системы случайных величин или случайные векторы п. 1. Основные понятия.
- •П. 2. Законы распределения свдт и свнт
- •Закон. Таблица распределения – закон распределения свдт.
- •Решение.
- •Решение.
- •Закон. Функция распределения – закон распределения свдт и свнт.
- •Решение.
- •3. Плотность распределения (для свнт)
- •Решение.
- •Решение.
- •П. 4. Плотности распределения отдельных величин, входящих в систему. Равномерное и нормальное распределения. Условные законы распределения
- •Решение.
- •Решение.
- •П. 5. Числовые характеристики системы. Корреляция. Линии регрессии
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •§ 9. Закон больших чисел. Предельные теоремы теории вероятностей
Решение.
Количество испытаний n = 243, количество успехов m = 70, вероятность успеха р = 0,25, вероятность неудачи q = 1 – 0,25 = 0,75.
По формуле Бернулли считать сложно. Так как n и m велики, поэтому применим формулу Муавра - Лапласа.
Найдем сначала x и f(x):
![]() ,
тогда
,
тогда
![]() .
.
Можно было не считать значение f(1,37) напрямую, а обратиться к таблице в учебнике.
Подставим найденное значение f(1,37) в формулу:
P243(70) =
![]() .
.
3. Предельная интегральная теорема Муавра - Лапласа (асимптотическая формула для случая, когда число успехов m лежит в некоторых пределах)
Теорема 1. Если m
– число наступлений события А в
n независимых испытаниях,
в каждом из которых вероятность этого
события равна р (0 < p
< 1), то равномерно относительно a
и b (![]() )
при
имеет место соотношение:
)
при
имеет место соотношение:
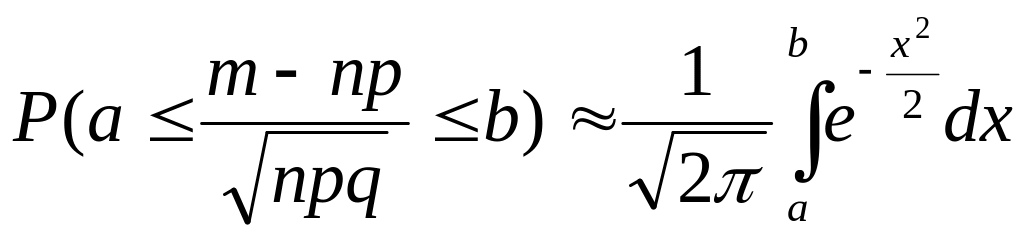 .
.
В некоторых источниках
![]() или
или
![]() .
.
Ранее вывели, что
![]() .
Численное значение нашего интеграла
можно найти с помощью таблиц (стр. 406 в
задачнике Ефимова – Демидовича) для
функции Лапласа Ф(x):
.
Численное значение нашего интеграла
можно найти с помощью таблиц (стр. 406 в
задачнике Ефимова – Демидовича) для
функции Лапласа Ф(x):
![]() ,
где Ф(–x)
= 1 – Ф(x). Для тех
значений x, которых
нет в таблице, т.е для
,
где Ф(–x)
= 1 – Ф(x). Для тех
значений x, которых
нет в таблице, т.е для
![]() ,
Ф(x) = 1.
,
Ф(x) = 1.
Либо, функция Лапласа может быть в виде:
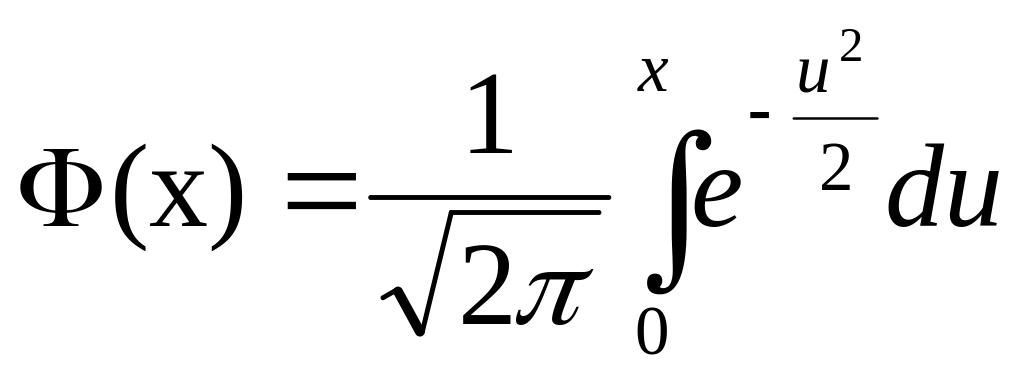 ,
где Ф(–x)
= – Ф(x), для тех
значений x, которых
нет в таблице, т.е. для
,
где Ф(–x)
= – Ф(x), для тех
значений x, которых
нет в таблице, т.е. для
![]() ,
Ф(x) =
,
Ф(x) =
![]() .
.
Теорема 2. (Теорема Муавра-Лапласа) Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < p < 1), событие А наступит не менее m1 раза и не более m2 раз приближенно равна:
![]() ,
,
где Ф(x) – функция
Лапласа, значения
![]() ,
,
![]() .
.
Теорема 3. (Закон больших чисел или теорема Бернулли).
При неограниченном увеличении числа однородных независимых опытов частота события будет сколь угодно мало отличаться от вероятности события в отдельном опыте.
Иначе, вероятность того, что отклонение
относительной частоты наступления
события А (![]() )
от постоянной вероятности события
А (р)
очень мало при
стремится
к 1.
)
от постоянной вероятности события
А (р)
очень мало при
стремится
к 1.
![]()
Доказательство.
![]()
![]()
![]() (разделим
все части неравенства на положительное
число
(разделим
все части неравенства на положительное
число
![]() )
=
)
=
![]() (по
теор. 1)
(по
теор. 1)
![]()
![]() .
.
Пример. Вероятность появления события А в каждом из 100 независимых испытаний постоянна и равна 0,8. Найти вероятность того, что событие появиться не менее 75 раз и не более 90 раз.
Решение.
Количество испытаний n = 100, вероятность успеха р = 0,8, вероятность неудачи q = 1 – 0,8 = 0,2 , m1 = 75, m2 = 90.
Найдем
![]() :
:
![]() ,
,
![]() .
.
По теореме 2:
![]()
![]() (по
таблице для функции Лапласа) = 0,9938 –
1+0,8944 = 0,8882.
(по
таблице для функции Лапласа) = 0,9938 –
1+0,8944 = 0,8882.
П. 4. Наивероятнейшее число появления события в независимых испытаниях
Определение 28. Число
![]() наступления события в независимых
испытаниях, в каждом из которых вероятность
появления события А равна р,
называется наивероятнейшим, если
вероятность того, что событие наступит
в этих испытаниях
раз превышает
или, по крайней мере, не меньше вероятности
остальных возможных исходов испытаний.
наступления события в независимых
испытаниях, в каждом из которых вероятность
появления события А равна р,
называется наивероятнейшим, если
вероятность того, что событие наступит
в этих испытаниях
раз превышает
или, по крайней мере, не меньше вероятности
остальных возможных исходов испытаний.
Наивероятнейшее число определяется из двойного неравенства:
![]() ,
,
причем 1) если
![]() дробное,
то существует одно
,
2) если
целое,
то существует два наивероятнейших
числа, 3) если
дробное,
то существует одно
,
2) если
целое,
то существует два наивероятнейших
числа, 3) если
![]() целое,
то
целое,
то
![]() .
.
Пример. Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которые выдержат испытание и вероятность этого числа.
