Решение.

Событие А произошло. Шар мог быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: .

Найдем вероятности событий:

(две урны состава Н₁ из пяти), , ,

(в каждой урне состава Н₁ 2 белых шара из пяти),

, .

По формуле Байеса найдем условную вероятность :

.

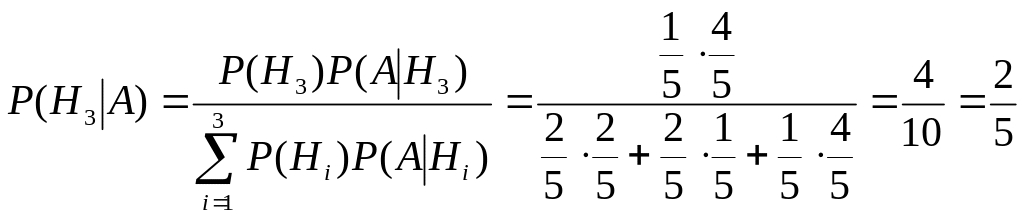§ 6. Последовательность независимых испытаний п. 1. Независимые испытания

Под испытанием станем понимать осуществление определенного комплекса условий, в результате которого может произойти то или иное элементарное событие пространства элементарных событий.

Определение 26. Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А.

В каждом испытании вероятность появления события А одинакова.

Ряд задач связан с экспериментом, в котором проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.

Рассматривается последовательность n независимых испытаний, под которой будем понимать дискретное новое пространство элементарных исходов, состоящее из точек (е¹, е², …, е^s,…, еⁿ), где е^s – произвольная точка пространства, отвечающая испытанию с номером s. В каждом испытании может произойти один из k исходов: или или …. .

– i –тый исход в s-том испытании, где i = 1, 2,…, k; s = 1, 2,…, n.

Пример. Пусть испытание состоит в подбрасывании игральной кости. Пространство элементарных событий состоит из шести точек: , т.е. шесть исходов. Если провести три испытания, то пространство состоит из 216 точек.

Обычно исходы обозначали большими заглавными буквами. Переобозначим!

Пусть происходит n независимых испытаний: 1, 2,…, s,…, n. В каждом испытании может произойти k исходов: 1-ый, 2, 3,…, i,…, k-ый.

Обозначим событие – i –тый исход в s-том испытании, где i = 1,2,…,k; s = 1, 2,…, n.

Эти k исходов – несовместные случайные события. Тогда для s-ого испытания можем записать: , причем Ø.

Обозначим вероятность i –ого исхода при s-том испытании через .

Пусть при первом испытании произошло событие под номером i₁, при 2-ом – событие под номером i₂, …, при n-ом – событие под номером i_n. Результат сразу n испытаний – событие, которое обозначим через произведение событий – цепочка результатов отдельных испытаний. . Данное событие – цепочка состоит из всех точек (е¹, е², …, е^s,…, еⁿ) пространства , для которых е¹ , е² , …, еⁿ .

Испытания – независимые, следовательно, по теореме 4, имеет место равенство:

В случае, когда вероятности событий не зависят от номера испытаний, ,

В силу несовместности и единственной возможности исходов, очевидно, что , так как .

Теорема. Если данные n испытаний независимы, то любые m из них также независимы.

Теорема. Для того, чтобы n испытаний были независимы, необходимо и достаточно выполнения условия:

,

для любой группы чисел s, s₁, s₂,…,s_m (1 < s, s₁, s₂,…,s_m < n) и любых m, i, i₁, i₂,…, i_m, .