2.5.5 Look through the text and find the English equivalents for the following Russian phrases and word-combinations:

в каждый последующий интервал времени; за единицу времени; изменяется равномерно; постоянно изменяется; означает среднее ускорение; уравнения выше; в обоих случаях.

2.5.6 Read and translate the text, give brief difinitions to angular velocity, angular acceleration, rotary inertia and explain Newton’s second law for rotary motions.

Rotary motions

Angular Velocity. — Let one end of a line ОA of Figure 18 be fixed, and then let the line revolve in a plane about this fixed end. The rate at which the line rotates is called its angular velocity which is usually expressed in radians per second. If the rate of rotation of the line is constant, the angular velocity is constant and is equal to the angle through which the line turns in unit time. The angular velocity may also be measured in revolutions per second or per minute. Angu­lar velocity like linear velocity is a vector quantity. It can be repre­sented by drawing a line of suitable length in the direction of the axis about which the rotation takes place.

Angular Acceleration. — The rate at which the angular velocity changes is called the angular acceleration. It is the increase or de­crease in angular velocity per unit of time. It is related to the angular velocity in the same way in which the linear acceleration is relat­ed to linear velocity. In an angular acceleration as in linear accelera­tion it is necessary to specify two units of time. One of these units gives the unit of time in which the angular velocity is measured, and the other gives the unit of time used to measure the change in the angular velocity. Ordinarily, the same unit of time is used in both cases.

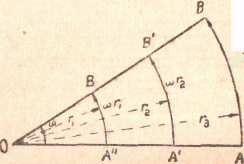
Figure 18 - Relation between angular velocity and linear velocity.

An­gular velocity times radius gives linear velocity

Relation of Torque to Angular Ac­celeration. — In order to produce linear acceleration, it is necessary to apply a force to the body, and the greater the force the greater the acceleration. To produce angular acceleration, it is necessary to apply a torque to the body. The greater the torque, the greater is the angular acceleration that is pro­duced. For a particular body rotating about a fixed axis, it is found that the angular acceleration is proportional to the torque that produ­ces it. This factor of proportionality by which the angular acceleration must be multiplied in order to give the torque is a measure of the opposition of the body to being set in rotation. It is analogous to the mass of a body, which is a measure of the opposition of a body to being set in translation. The relation between the torque and the angular acceleration can be expressed by the equation

T = IA

where A = the angular acceleration in radians per second per second; T = the torque (force in poundals and distance in feet, or force in dynes and distance in centimeters); I = the factor of proportionality called the rotary inertia.

This relation is known as Newton’s second law for rotary motions. It states that the angular acceleration is proportional to the torque.

Rotary Inertia. — Experiment has shown that the opposition of a body to being set in translation is proportional to the mass of the body and does not depend on anything else. It is found, however, that the opposition which a body offers to being set in rotation, or accel­erated, about a fixed axis depends not only on the mass but also on the way in which this mass is distributed about the axis. This opposi­tion which is called the rotary inertia, or the moment of inertia, is proportional to the mass and to the square of the distance of the mass from the axis of rotation. For this reason, when it is desired to make the rotary inertia of a flywheel of given mass as large as possible, the mass of the wheel is concentrated in the rim. When the mass is con­centrated near the axis, the tendency of the wheel to continue in mo­tion, or its resistance to being set in motion, is much less. In order to calculate the rotary inertia, multiply each element of mass by the square of its distance from the axis of rotation, and then add together all these products.

2.5.7 Read the text, translate it and answer the questions: In what way can we find the acceleration when acting force is variable? What is SHM? What is periodic motion? What is oscillatory motion? What is the period of the motion?

Harmonic motion

Now we are to study the motion of a body when the resultant force on it is not constant, but varies during the motion. Naturally, there are an infinite number of ways in which a force may vary and hence no general expression can be given for the motion of a body when acted on by a variable force, except that the accelaration at each instant must equal the force at that instant divided by the mass of the body. There is, however, one particular mode of variation which is met with in practice so frequently that it is worth while to develop formulas for this special case. The force referred to is an elastic restoring force, brought into play whenever a body is distorted from its normal shape. When released, the body will be found to vibrate about its equilibrium position.

The example of this sort of motion is given below.

Suppose that a flat strip of steel is clamped vertically in a vice and a small mass is attached to its upper end as in Figure 19.

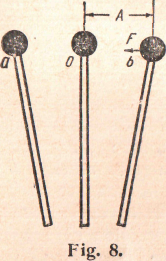
Figure 19 - A flat strip of steel

We shall assume that the strip is sufficiently long and the displace­ment sufficiently small so that the motion is essentially along a straight line. The mass of the strip itself is negligible.

Let the top of the strip be pulled to the right a distance A as in Figure 19 and released. The attached mass is then acted on by a re­storing force exerted by the steel strip and directed toward the equi­librium position O. It therefore accelerates in the direction of this force, and moves on toward the center with increasing speed. The rate of increase (i. e. the acceleration) is not constant, however, since the accelerating force becomes smaller as the body approaches the center.

When the body reaches the center the restoring force has decreased to zero, but because of the velocity which has been acquired, the body overshoots the equilibrium position and continues to move to­ward the left.

As soon as the equilibrium position is passed the restoring force again comes into play directed now toward the right. The body therefore decelerates and it will therefore be brought to rest at some point to the left of O, and repeat its motion in the opposite direction.

Both experiment and theory show that the motion will be con­fined to a range + A on either side of the equilibrium position, each to-and-fro movement taking place in the same length of time.

Were there no loss of energy by friction the motion would con­tinue indefinitely once it had been started. This type of motion, under the influence of an elastic restoring force and in the absence of all friction, is called simple harmonic motion, often abbreviated SHM.

Any sort of motion which repeats itself in equal intervals of time is called periodic, and if the motion is back and forth over the same path it is also called oscillatory.

A complete vibration or oscillation means one round trip, say from α to b and back to α.

The periodic time, or simply the period of the motion, represented by T, is the time required for one complete vibration.

The frequency, f, is the number of complete vibrations per unit time.

Evidently the frequency is the reciprocal of the period or

T = l:f

The displacement, x, at any instant, is the distance away from the equilibrium position or center of the path at that instant.

The amplitude, A, is the maximum displacement. The total range of the motion is therefore 2 A.