Вводная к лабораторной работе №1

Рассмотрим возможности Mathcad для решения дифференциальных уравнений.

Запишем пример.

Это диф. ур-е описывает некоторую неизвестную функцию. здесь производная некой неизвестной функции по переменной . Проинтегрируем его, чтобы найти :

Решение этого диф. ур-я нам даёт некое семейство функций. Чтобы найти конкретную функцию, нужно задать начальное условие :

Нужно найти константу .

Подставляем в решение вместо :

Подставляем конкретное найденное в решение диф. ур-я и получаем искомую функцию:

Построим график получившейся функции:

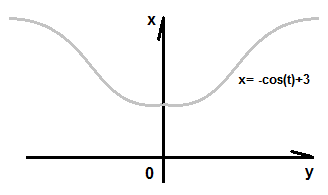
Так обстоит дело с решением простого дифференциального уравнения.

В Mathcad мы будем искать численное решение диф. ур-й, результатом будет таблица значений аргумента и функции, по которой в Mathcad можно легко построить график.

Запишем наш пример на синтаксисе системы Mathcad.

Зададим начальное условие:

Решаемое диф. уравнение (первого порядка) должно быть разрешено относительно производной. Левая часть диф. уравнения не задаётся, по умолчанию в левой части у нас всегда находится первая производная. Всё различие между диф. уравнениями будет заключаться в правой части. Задаётся правая часть диф. уравнения:

– в параметрах функции сначала указываем имя независимой переменной ( ), а потом – имя искомой функции ( ).

После задания правой части и начального условия мы вызываем собственно систему численного решения дифференциальных уравнений. Наиболее эффективным численным методом решения диф. ур-я является метод Рунге-Кутта. Рунге и Кутт – два немецких математика, разработавшие данный метод в конце XIX века. Существовало целое поколение программистов, которые программировали этот метод. Теперь этот метод встроен практически во все математические пакеты.

где – это начальное условие, которые мы задали заранее. В системе Mathcad начальное условие можно указывать прямо в скобках в качестве параметра функции (в явном виде).

– это отрезок интегрирования. Мы выбрали отрезок от 0 до , т. к. наша функция периодическая, и её период равен .

30 – число разбиения отрезка интегрирования. Как мы знаем, для нахождения численного решения интеграла, мы разбиваем отрезок на несколько частей и на каждом участке аппроксимируем исходную функцию некой параболой (метод Симпсона), хордой или прямоугольником. Чем больше частей, тем ближе значение интеграла к аналитическому решению. Длина каждого отрезка в нашем случае равна , т. е. порядка 2.

– это функция, составляющая правую часть нашего диф. ур-я. Без этого параметра Mathcad не будет знать, какое же диф. ур-е мы решаем.

означает фиксированный шаг.

Чтобы получить ответ, достаточно ввести следующую строчку:

Результат мы получим в виде таблицы из 30 строк (по одному на каждый отрезок разбиения) и двух столбцов, где первый столбец – это значение , а правый – значение .

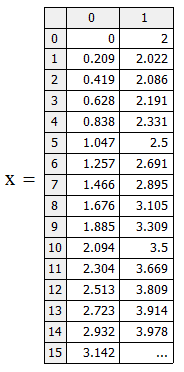
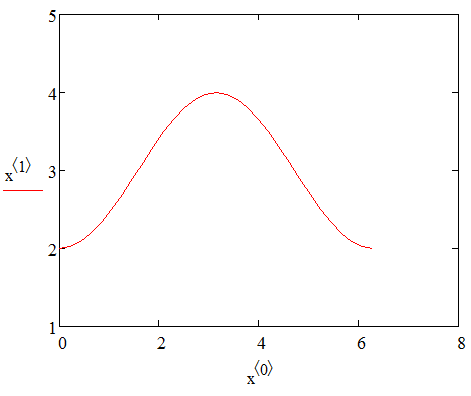
В этой таблице столбик со значениями имеет наименование , а столбик со значениями имеет наименование . Поэтому чтобы построить график найденной функции , нам нужно вызвать декартову плоскость, а затем обозначить левую ось , а нижнюю ось – . Для того чтобы создать треугольные скобочки в степени, нужно набрать , а затем щёлкнуть комбинацию клавиш .

05.04.2012 Практика

ЛАБОРАТОРНАЯ РАБОТА №1

Получим численное решение моделей Мальтуса и Ферхюльста и строим их графики.

Решение в файле Учебные материалы\Мат. моделирование\01. Мальтус и Ферхюльст.xcmd.

11.04.2012 Практика

ЛАБОРАТОРНАЯ РАБОТА №2

Моделируем систему “хищник – жертва”:

В отличие от предыдущих моделей здесь мы имеем систему двух дифференциальных уравнений от двух элементов. В Mathcad мы моделируем эту систему с матричной точки зрения. Матрица будет состоять из двух столбцов, где первый столбец будет описывать первое диф. ур-е, а второй – второе. Отныне под мы подразумеваем не скалярную величину, а векторную, как столбец двух переменных.

– коэффициент репродукции хищников

– коэффициент каннибализма хищников в результате бескормицы

– смертность жертв после встречи с хищниками

– аппетиты хищников

Работа была выполнена и сохранена в файл Учебные материалы\Мат. моделирование\02. Хищник – жертва.xcmd.

В результате работы был сделан следующий вывод: экстремальное значение численности каждой из популяций приходится на тот момент, когда скорость изменения численности другой популяции становится постоянной.

13.04.2012 Практика

ЛАБОРАТОРНАЯ РАБОТА №3

Решение в файле Учебные материалы\Мат. моделирование\03. Затухающие химические процессы.xcmd.

16.04.2012 Практика

ЛАБОРАТОРНАЯ РАБОТА №4

Построим модель колебаний математического маятника при малых углах, при больших углах и общую модель. Варьируем начальные условия ( угол, начальная скорость). Построим ременную и фазовую диаграммы.

Транслируем нашу систему уравнения из математической нотации в нотацию Mathcad:

Где – это начальный угол в радианах, а – начальная скорость.

Всякая модель имеет свою ограниченную область применимости: начальные углы и скорости должны быть таковы, чтобы крайние положения маятника не превышали порядка одного радиана.

Чтобы построить общую модель без упрощений, приведём исходное диф. уравнение 2-го порядка к системе двух диф. ур-й первого порядка. Величина в нашем исследовании является константой, обозначим её просто w.

Решение в файле Учебные материалы\Мат. моделирование\04. Колебания математического маятника.xmcd

18.04.2012 Лекция

КЛАССИФИКАЦИЯ ОСОБЫХ ТОЧЕК

СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

ПЕРВОГО ПОРЯДКА

В основе классификации лежит исследование поведения систем в окрестностях особой точки.

Пример:

Рассмотрим систему дифференциальных уравнений “Хищник – жертва”

– коэффициент репродукции хищников

– коэффициент каннибализма хищников в результате бескормицы

– смертность жертв после встречи с хищниками

– аппетиты хищников

Найдём особые точки – стационарные точки, в которых достигается динамическое равновесие, т. е. производные равны нулю.

Рассмотрим модель в окрестности точки

, ( , ). Произведение – это порядок малости по отношению к предыдущему слагаемому в правых частях уравнений системы. Этой величиной мы собираемся пренебречь. Отбросим из правых частей всё, что содержит произведения . Тогда наша система примет вид:

Для упрощения примем ,

Тогда:

Это гипербола.

Направление движения: слева направо.

Это точка типа “седло”

Таким образом, характер особой точки установлен путём линеаризации системы уравнений в окрестности особой точки и исследование полученной линейной системы.

Линеаризация – это отбрасывание в правых частях уравнений членов второго и более высоких порядков малости.

Теперь рассмотрим модель в окрестности точки

,

Для выяснения характера особой точки произведём в её окрестности линеаризацию данной системы. Однако замечаем, что в правых частях уравнений у нас не содержатся эти отношения. Поэтому следует передвинуть начало координат в точку . Для этого из и вычтем координаты .

Выразим координаты и в исходной модели через наши новые координаты:

Продифференцируем:

Раскроем скобки в первом уравнении и отбросим из него произведение , т. к. оно представляет собой второй порядок малости. Тогда первое уравнение принимает вид:

Представим как

Получаем:

Аналогично поступаем и со вторым уравнением, представив как . Получаем:

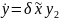
Получили систему

Решим её так же, как и в первом случае:

Получили эллипс.

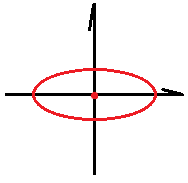
По виду линеаризованной системы определяем, в каком направлении движутся наши фазовые точки со временем на фазовой плоскости: против часовой стрелки.