
- •Общие понятия теории моделирования
- •Цели моделирования
- •Общая классификация моделей
- •Классификация идеальных моделей
- •Логико-математические модели
- •Компьютерные модели
- •Модель динамико-биологических популяций
- •Математическое моделирование химических процессов
- •Незатухающие колебательные процессы в химии
- •Затухающие колебания в химических процессах
- •Моделирование движения маятника
- •Вводная к лабораторной работе №1
- •Качественная теория динамических систем
- •Тримолекулярная модель (брюсселлятор)
- •Не существует
Затухающие колебания в химических процессах
Данная модель была рассмотрена в 1910 году тем же шведским химиком А. Д. Лотка.

Лотка реализовывал особый вид химической реакции для данной цепочки. Особенность её заключается в следующем: превращение вещества в вещество происходит путём химического взаимодействия вещества с продуктом своего распада .
Запишем кинетическое уравнение вещества , которое участвует в двух реакциях. Предполагаем, что вещество A находится в избытке.

 .
Вещество
не просто распадается, а распадается
путём взаимодействия с веществом своего
распада.
.
Вещество
не просто распадается, а распадается
путём взаимодействия с веществом своего
распада.
Обобщённая модель изменения концентрации вещества :
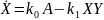
Запишем обобщённую модель изменения концентрации вещества , которое также участвует в двух реакциях:

Аналогично для вещества :
 .
.
Получаем следующую модель:
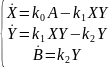
Из этой модели можем сделать вывод, что вещество B никак не влияет на динамику концентрации веществ и . Следовательно, вещество имеет смысл рассматривать уже после получения решения системы первых двух уравнений.

Найдём стационарные точки – точки, в которых скорость изменения концентрации равна нулю, т. е. концентрации постоянны во времени. Получим систему двух алгебраических уравнений:

 противоречит уравнению 1, а следовательно,
не является корнем системы.
противоречит уравнению 1, а следовательно,
не является корнем системы.
 в
уравнение 1.
в
уравнение 1.


Получили
координаты особой точки – (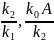 ).
).
В
этой особой точки мы получаем линейное
возрастание вещества
во времени:
 .
.
Выясним, как себя ведут фазовые траектории в этой особой точке. Начертим фазовую плоскость:
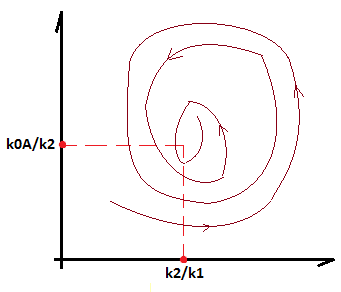
Для данной модели найденная особая точка имеет тип “фокус”. В окрестностях такой точки фазовые траектории не являются замкнутыми, в данном случае фазовые траектории стремятся к фокусу по спирали. Методологию этого вывода мы рассмотрим позже.
Фазовые траектории здесь бесконечно наматываются по спирали вокруг фокуса, но не достигают его.
В данной модели особая точка фокус является устойчивой. Это значит, что каковы бы ни были начальные условия реакции, все фазовые траектории будут стремиться по спирали к фокусу. Если бы фокус был неустойчивым, то фазовые траектории бы постоянно удалялись от него по спирали (стрелочки в обратную сторону).
Существуют системы двух нелинейных дифференциальных уравнений, которые имеют единственную особую точку, являющуюся неустойчивым фокусом. В этом случае фазовые траектории меняют направление на противоположное.
Больше моделировать химические реакции на лекциях мы не будем.
Моделирование движения маятника
Маятник – это колебание твёрдого тела относительно точки подвеса. Обычно маятник ассоциируется у нас с подвешенным на нити или проволоке грузом. Однако теперь мы не будем требовать существования некоторой нити. Маятник – это некое твёрдое тело, колеблющееся относительно точки подвеса , не совпадающей с центром масс данного твёрдого тела.
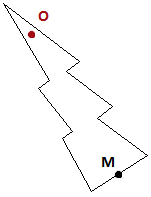
Запишем упрощающие предположения:
Сила трения в точке подвеса пренебрежимо мала
Сопротивление движению среды (вязкое трение) пренебрежимо мало (водород или разреженный воздух)
При движении тело маятника не деформируется.
Математическая цель нашего моделирования – установить связь между координатами центра масс и координатами точки подвеса в зависимости от времени. Это потребует нахождения двух функций. Однако эту задачу можно упростить. Превратим наш физический маятник в математический, полностью убрав всё ненужное. Оставим только точку подвеса и центр масс. Тогда точка центра масс будет жёстко привязана к точке подвеса, т. е. образуется та самая “нить”, которая нам в первую очередь приходит на ум, когда мы думаем о маятнике.

А
теперь опустим из точки подвеса вертикаль.
Эта вертикаль играет важную роль, ведь
колебания симметричны. Всё, что нам
остаётся – это следить за углом отклонения
нити
 от этой самой вертикали. Таким образом
мы приходим к выводу: построить
математическую модель функции
от этой самой вертикали. Таким образом
мы приходим к выводу: построить
математическую модель функции
 ,
которая определяет отклонение угла
нити
маятника от вертикали в зависимости от
времени. Тогда мы сможем найти и скорость
движения маятника – это производная –
,
которая определяет отклонение угла
нити
маятника от вертикали в зависимости от
времени. Тогда мы сможем найти и скорость
движения маятника – это производная –
 ,
вторая производная даст ускорение –
,
вторая производная даст ускорение –
 .
.
Единственная
сила, влияющая на это движение – это
сила тяжести:
 .
.
Момент
силы тяжести вычисляется по формуле
 ,
где
,
где
 – момент инерции тела относительно оси
вращения, а
– момент инерции тела относительно оси
вращения, а
 – это (по аналогии с
– это (по аналогии с
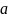 )
изменение скорости угла поворота, т. е.
его вторая производная:
)
изменение скорости угла поворота, т. е.
его вторая производная:
 .
.
Построим уравнение Ньютона и получим искомую математическую модель.
31.03.2012 Лекция |
Используем универсальные ньютоновские законы для движения маятника.
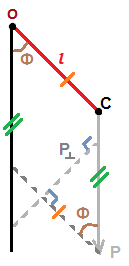
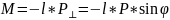



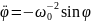
Получили
дифференциальное уравнение второго
порядка. Аналитически его проинтегрировать
невозможно, поэтому сформируем
обоснованные ожидания относительно
результата численного решения. Для
выявления общих свойств движения
маятника целесообразно рассмотреть
упрощённую модель движения – малые
колебания. Сделаем угол
 малым, т. е.
малым, т. е.
 .
Вспомним первый замечательный предел:
.
Вспомним первый замечательный предел:

Это
означает, что мы получили две эквивалентно
малые величины –
и
 .
Тогда заменим
на
.
Тогда наша модель примет вид:
.
Тогда заменим
на
.
Тогда наша модель примет вид:
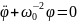
Данное дифференциальное уравнение уже можно проинтегрировать аналитически. Только вместо диф. ур-я второго порядка мы будем решать систему диф. ур-й первого порядка.

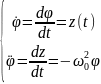
Это система линейных дифференциальных уравнений.
По-членно разделим второй уравнение на первое:

Получили диф. уравнение первого порядка с разделяющимися переменными. Решим его.



Замечаем, что C – это не такая уж и произвольная константа. Она не может быть отрицательной, т. к. сумма неотрицательных слагаемых в левой части не может быть отрицательной. Поэтому просто возведём C в квадрат.

Перенесём
 к первому слагаемому в качестве
знаменателя:
к первому слагаемому в качестве
знаменателя:
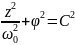
Получили каноническую форму записи уравнения эллипса.
Следовательно, математическое состояние маятника описывается точками этого эллипса.
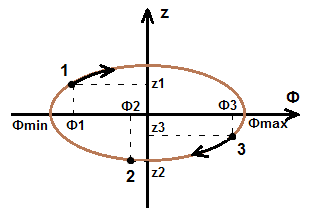
В
точке 1 скорость равна
 ,
а угол –
,
а угол –
 ,
в точке 2 скорость будет
,
в точке 2 скорость будет
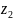 ,
а угол –
,
а угол –
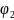 .
При отрицательном значении угла
скорость движения маятника будет
положительной – т. е. маятник будет
двигаться вправо, а при положительном
значении угла
скорость движения наоборот будет
отрицательной.
.
При отрицательном значении угла
скорость движения маятника будет
положительной – т. е. маятник будет
двигаться вправо, а при положительном
значении угла
скорость движения наоборот будет
отрицательной.
Это наша упрощённая модель движения маятника для малого угла, близкого к нулю.
Построим ещё одну упрощённую модель.
Второе
упрощающее предположение: движение
маятника происходит в окрестности угла
 .
Маятник в этом случае будет принимать
неустойчивые положения.
.
Маятник в этом случае будет принимать
неустойчивые положения.
 ,
,

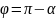

По формулам приведения получаем:

Дважды проинтегрируем , получим:


Получили также дифференциальное уравнение второго порядка. Преобразуем его в систему диф. ур-й первого порядка аналогично тому, как делали в прошлый раз:


По-членно разделим второе уравнение на первое
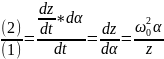



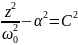
Получили
каноническую форму записи уравнения
гиперболы. Центр гиперболы будет
находиться в точке
 .
В точке
.
В точке
 будет строго аналогичная картина.
будет строго аналогичная картина.

На
фазовой плоскости
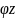 выделяются две области: под асимптотами
область 1, в которой располагаются
эллипсоподобные траектории движения
маятника, и область 2, в которой расположены
вращательные траектории движения
маятника.
выделяются две области: под асимптотами
область 1, в которой располагаются
эллипсоподобные траектории движения
маятника, и область 2, в которой расположены
вращательные траектории движения
маятника.
04.04.2012 Практика |
