
- •1. Линейная алгебра и аналитическая геометрия
- •2. Дифференциальное и интегральное исчисления
- •3. Функции нескольких переменных
- •4. Дифференциальные уравнения
- •5. Ряды
- •6. Теория вероятностей
- •1. Линейная алгебра и аналитическая геометрия Задача 1. Дана система линейных неоднородных алгебраических уравнений
- •2. Дифференциальное и интегральное исчисления
- •3. Функции нескольких переменных
- •4. Дифференциальные уравнения
- •5. Ряды
- •6. Теория вероятностей
6. Теория вероятностей
Задача 17. Имеется 6 одинаковых шаров, занумерованных числами 1, 2, 3, 4, 5, 6. Наудачу раскладываем эти шары в 3 коробки по 2 шара. Найти вероятность того, что в каждой коробке окажется один нечётный шар и один чётный.
Решение.
Опыт состоит в том, что 6 шаров наудачу
раскладываем по 2 шара в 3 коробки. Все
исходы опыта равновозможны и их число
n
конечно. Следовательно, можем применить
классическую формулу вероятности
![]() ,
где А
– событие, состоящее в том, что в каждой
коробке окажется один нечётный шар и
один чётный, а m
– число всех исходов, благоприятствующих
событию А.
,
где А
– событие, состоящее в том, что в каждой
коробке окажется один нечётный шар и
один чётный, а m
– число всех исходов, благоприятствующих
событию А.
Найдём n
– число всех исходов опыта. Выбрать 2
шара из 6-ти в I-ю
коробку можно
![]() способами. Из оставшихся 4 шаров выбрать
2 шара во II-ю
коробку можно
способами. Из оставшихся 4 шаров выбрать
2 шара во II-ю
коробку можно
![]() способами. Оставшиеся после этого 2 шара
попадут в III-ю
коробку (
способами. Оставшиеся после этого 2 шара
попадут в III-ю
коробку (![]() ).
Число всех исходов опыта равно
).
Число всех исходов опыта равно
![]() .
По формуле
.
По формуле
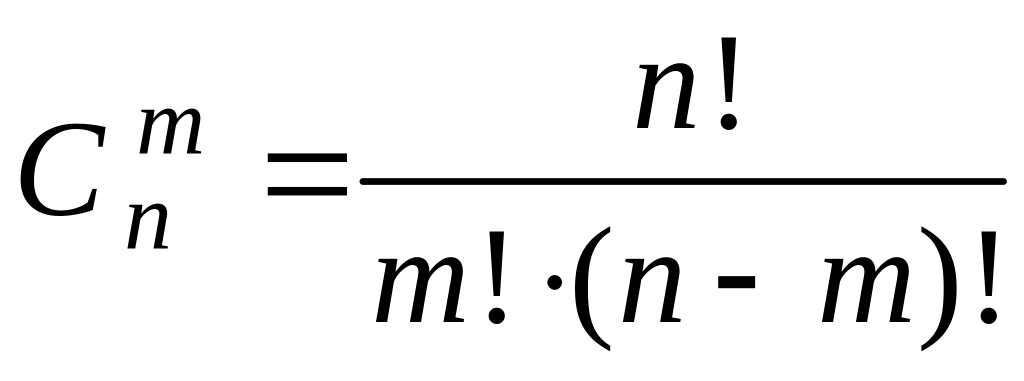 вычислим
вычислим
![]()
Найдём m
– число исходов, благоприятствующих
событию А.
Выбрать нечётный шар в I-ю
коробку можно
![]() способами, чётный –
способами. Следовательно, число всех
благоприятствующих пар шаров для I-й
коробки равно
способами, чётный –
способами. Следовательно, число всех
благоприятствующих пар шаров для I-й
коробки равно
![]() Обозначим сказанное схематично:
Обозначим сказанное схематично:
![]() .
.
Аналогично найдём число благоприятствующих пар шаров для II-й коробки из оставшихся 4 шаров:
![]() .
.
Для III-й коробки
![]() .
.
Тогда
![]() ,
,
![]() .
.
Искомая вероятность равна 0,4.
Задача 18. Три студента сдают экзамен. Для них приготовлены три билета: №1, №2, №3. Первый студент наудачу возьмёт любой билет, второй выберет наудачу один из двух оставшихся, третий заберёт оставшийся. Для каждого из студентов найти вероятность извлечь билет №1.
Решение.
Пусть А1,
А2,
А3
– события, состоящие в том, что
соответственно 1-й, 2-й и 3-й студент
извлечёт билет №1. Требуется найти
![]() .
.
Очевидно, что
![]() Найдём
Найдём
![]() .
Первый студент взял один билет. Второму
осталось два билета. Обозначим гипотезы:
.
Первый студент взял один билет. Второму
осталось два билета. Обозначим гипотезы:
Н1 – билет №1 уже извлечён; Н2 – билет №1 ещё не извлечён.
Н1,
Н2
– полная группа событий ( сумма этих
событий – достоверное событие и они не
могут произойти одновременно).
Следовательно, по формуле полной
вероятности
![]()
Очевидно, что
![]() так как гипотеза Н2
означает что 1-й студент не взял билет
№1. Итак,
так как гипотеза Н2
означает что 1-й студент не взял билет
№1. Итак,
![]()
![]()
Найдём Р(А3).
![]() .
.
Уже вычислено
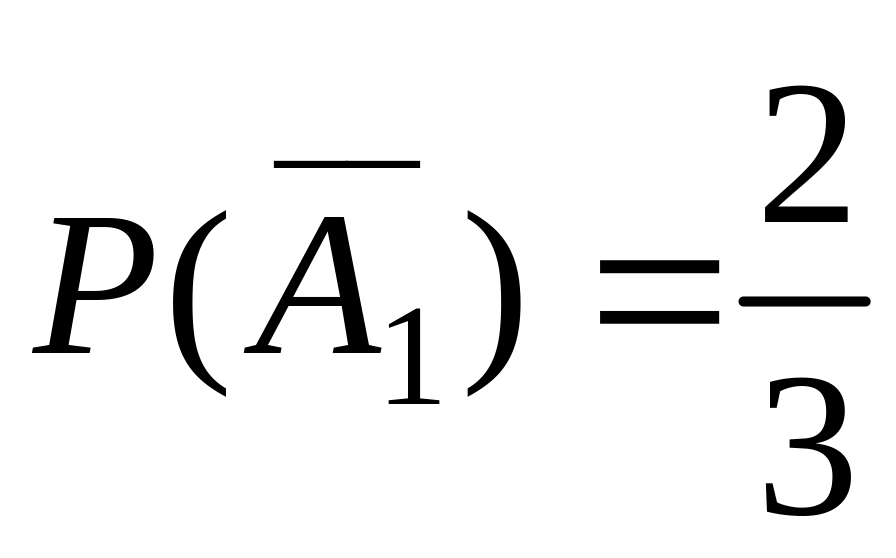 .
Условная вероятность
.
Условная вероятность
![]() – это вероятность того, что 2-й студент
не взял билет №1 при условии, что 1-й
студент не взял билет №1, то есть
вероятность не взять билет №1 из двух
билетов, среди которых есть этот №1.
Получаем
– это вероятность того, что 2-й студент
не взял билет №1 при условии, что 1-й
студент не взял билет №1, то есть
вероятность не взять билет №1 из двух
билетов, среди которых есть этот №1.
Получаем
![]() .
В результате
.
В результате
![]() .
.
Все искомые
вероятности найдены:
![]()
Задача 19. MN – средняя линия треугольника АВС, MN АВ. На треугольник АВС наудачу поставлены три точки. Случайная величина Х равна числу точек, попавших на треугольник MBN. Построить ряд распределения этой случайной величины.
Решение. Случайная величина Х может принимать значения х1 = 0, х2 = 1,
х3 = 2, х4 = 3. Найдем вероятность появления каждого из этих значений.
 Так
как MN
– средняя линия
АВС,
то
Так
как MN
– средняя линия
АВС,
то
![]() .
.
Вероятность того, что точка, наудачу поставленная на
АВС,
попадёт на
MВN
равна
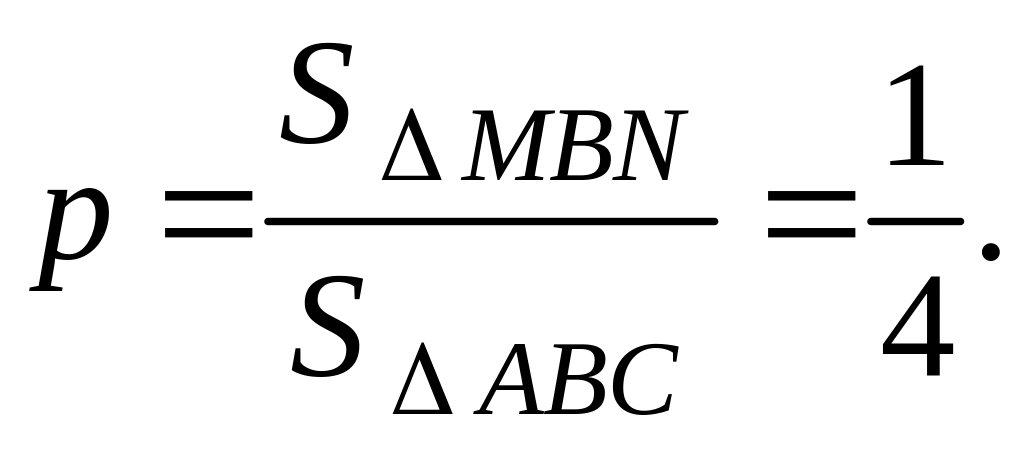
Это испытание (наудачу ставим точку на АВС) повторяем 3 раза. Вероятность того, что в n = 3 испытаниях событие (попадание точки на MВN ) произойдёт ровно k раз вычислим по формуле Бернулли:
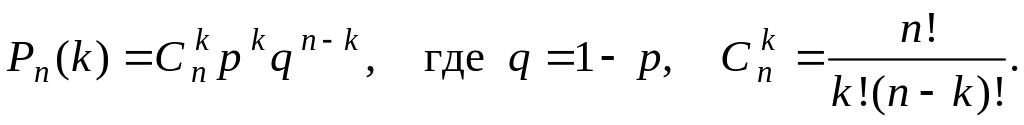
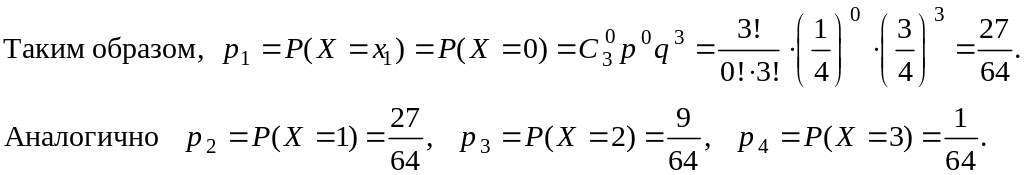
хk
0
1
2
3
pk
![]()
![]()
![]()
Построим искомый ряд распределения .
Задача 20. Задан ряд распределения дискретной случайной величины Х. Найти неизвестный параметр С, математическое ожидание M(X), дисперсию D(X), среднее квадратическое отклонение и вероятность P(a < X < b).
хk
–5
–2
4
7
pk
0,4
С
0,35
0,1
a
= – 3,
b
= 6.
Решение. Сумма вероятностей всех возможных значений Х равна единице. Следовательно, 0,4 + С + 0,35 + 0,1 = 1, С = 0,15.
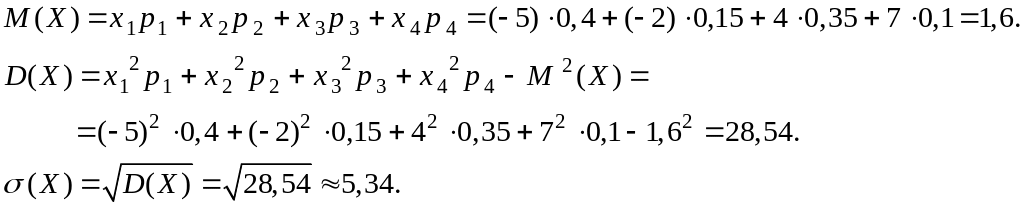
![]()
![]()
![]() Таким образом
найдены
Таким образом
найдены
![]()
Задача
21. Задана
плотность распределения непрерывной
случайной величины Х.
Найти неизвестный параметр С,
математическое ожидание M(X),
дисперсию D(X),
среднее квадратическое отклонение
и вероятность P(a
< X
< b).
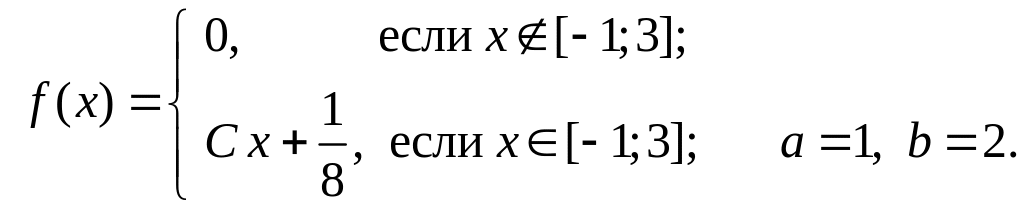
Решение.
Плотность распределения непрерывной
случайной величины удовлетворяет
условию
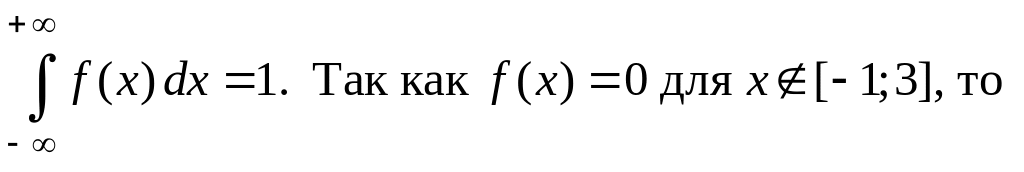

СОДЕРЖАНИЕ
Введение 3
Общие рекомендации студентам по работе над контрольной работой 3
Вопросы к экзамену по курсу “Высшая математика” 4
Литература 9
Задания для контрольных работ 9
Методические указания к решению типовых задач 23
Тема 1. Линейная алгебра и аналитическая геометрия 23
Тема 2. Дифференциальное и интегральное исчисления 27
Тема 3. Функции нескольких переменных 34
Тема 4. Дифференциальные уравнения 35
Тема 5. Ряды 37
Тема 6. Теория вероятностей 40
