Практическая работа № 7 Построение интегральных критериев в q-нормальной форме

_{Цель работы: Определение закона аппроксимации интегрального критерия.}

_{Нормальную форму интегрального критерия можно представить в виде}

или

(u) = _n(u_n) + _n-1(u_n, u_n-1) + … + ₁(u_n, u_n-1, …, u₁).

Можно зафиксировать значение (u) = e_j = const, тогда множество значений составляющих вектора u⁽ⁱ⁾ образует поверхность размерностью (n – 1), называемую поверхностью безразличия, каждая точка которой имеет одинаковое значение интегрального критерия.

Если в пространстве критериев провести не одну, а несколько поверхностей безразличия, то, анализируя их взаимное расположение, можно выяснить вид функции _n(u) в Q-нормальной форме и закон, с помощью которого можно аппроксимировать поведение функции _n(u) вдоль координатной оси и_n для каждого фиксированного вектора u^(n-1).

Линейная аппроксимация

Если значение _n(u) изменяется вдоль координатной оси u_n по линейному закону, тогда

_n(u^(n-1), u_n) = k₀(u^(n-1)) + k₁(u^(n-1))u_n, то есть _n(u) = k₁(u^(n-1), u_n(j))+e_j

и для значения e_j < _n(u) < e_j+1

,

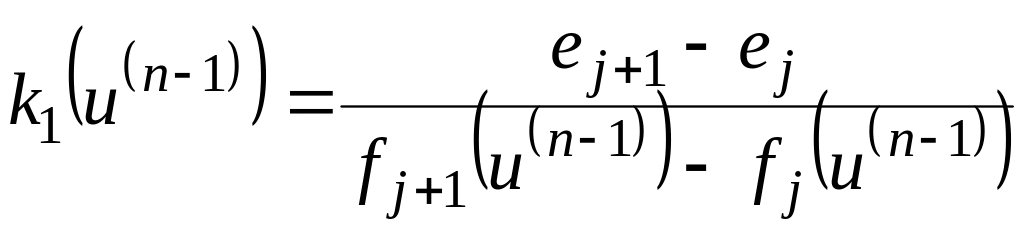то есть значение k₁(u^(n-1)) обратно пропорционально расстоянию между поверхностями Q_j+1 и Q_j, измеренному вдоль координатной оси и_n, что соответствует разности u_n(j + 1) – u_n(j) на рис. 7.1.

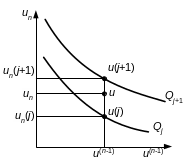
Рис. 7.1. Поверхности безразличия

То есть поверхности безразличия представляют собой семейство параллельно расположенных в пространстве Uⁿ гиперплоскостей и интегральный критерий принимает вид линейной формы. Отсюда следует, что k₁(u^(n-1)) = k₁ = const, если отношение u_n(j+1) к u_n(j) не зависит от значений компонент вектора u^(n-1). Взаимное расположение поверхностей Q_j, и Q_j+1 для этого случая показано на рис. 7.2а.

Аппроксимация логарифмической функцией

В этом случае _n(u) вдоль оси и_п изменяется по закону

_n(u) = k₀(u^(n-1)) + k₁(u^(n-1))ln(u_n), то есть (u) = k₁(u^(n-1))[ln(u_n) – ln(f₁(u^(n-1))]+e_j и для значения e_j < _n(u) < e_j+1

.

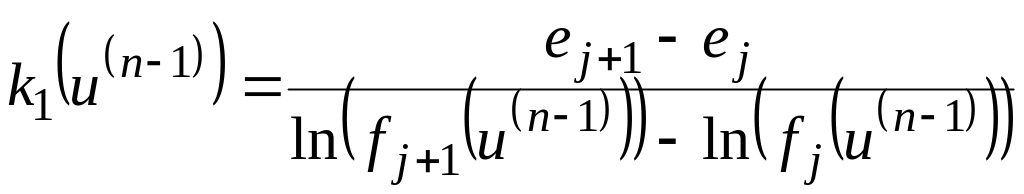Взаимное расположение поверхностей Q_j, и Q_j+1 для этого случая показано на рис. 7.2б.

Рис. 7.2. Взаимное расположение кривых безразличия при k₁(u₁) = const

и линейном (а), логарифмическом (б), показательном (в) и степенном (г)

законах аппроксимации функции _n(u)

Аппроксимация показательной функцией

Если в области u(j, j+1) определена _n(u) = k₀(u^(n-1)) + k₁(u^(n-1))exp(u_n), то есть (u) = k₁(u^(n-1))[exp(u_n) – exp(f_j(u^(n-1))] + e_j, тогда для e_j < _n(u) < e_j+1

.

При этом k₁(u^(n-1)) = k₁ = const, если для любого u^(n-1) разность значений показательной функции в точках f_j+1(u^(n-1)) и f_j (u^(n-1)) остается неизменной, как это показано на рис. 7.2в.

Аппроксимация степенной функцией

Пусть функция _n(u) имеет вид , то есть , откуда

.

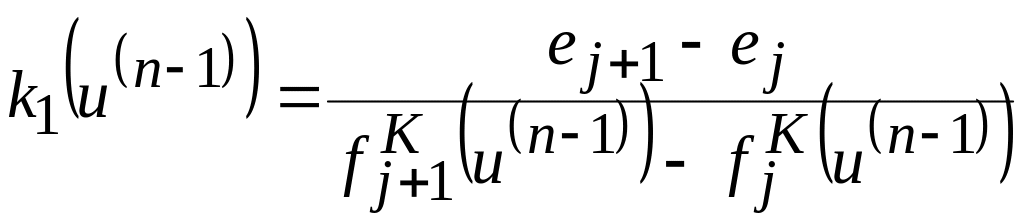На рис. 7.2г показано взаимное расположение двух поверхностей безразличия для случая, когда K = 0,5 и k₁(u^(n-1)) = k₁ = const.

Выбор закона аппроксимации

Если закон аппроксимации заранее известен, то, имея достаточное число поверхностей безразличия, можно построить интегральный критерий на основе Q-нормальной формы. В простейших случаях для этого требуется всего две поверхности безразличия, причем особенности их взаимного расположения, как это видно из рис. 7.2, могут подсказать закон аппроксимации.

В противном случае необходимо определить закон опытным путем. Для этого в области U(j,j+1), ограниченной двумя поверхностями безразличия, выбирают произвольную точку и проводят через нее дополнительную поверхность безразличия . Затем, задавая различные законы аппроксимации функции _n(u), получают соответственно различные формы интегрального критерия. Для каждой такой формы определяют значение и поверхность безразличия , проходящую через точку и описываемую уравнением .

Чем меньше различаются между собой поверхности и , тем точнее принятый закон аппроксимации описывает систему предпочтений ЛПР. Если различия между и не превышают допустимой в данной задаче погрешности, то этот закон может быть использован для построения интегрального критерия. В противном случае следует попытаться отыскать другой закон аппроксимации функции _n(u) в области U(j, j+1), проводя, если надо, дополнительные поверхности безразличия между Q_j и Q_j+1. В наиболее сложных ситуациях функцию _n(u) приходится аппроксимировать полиномом, подбирая его степень так, чтобы обеспечить достаточную точность оценки предпочтительности с помощью соответствующего интегрального критерия.

Пример

Пусть необходимо упорядочить по предпочтительности телевизоры из множества S = [u¹ = (27; 100), u² = (35; 170), u³ = (45, 240), u⁴ = (58, 300)], оцениваемые по критериям u₁ – размер экрана (см) и и₂ – цена (руб.).

Для упрощения будем пользоваться вместо критерия u₂ критерием u₂ = 400 – u₂, характеризующим экономию покупателя при приобретении данного телевизора по сравнению с максимально допустимой ценой 400 руб. Тогда оба критерия (u₁ и u₂) будут соответствовать принципу «чем больше, тем лучше».

На рис. 7.3 построены множество S и кривые безразличия Q₁ и Q₂, полученные на основании опроса ЛПР, указавшего две эквивалентные последовательности векторных оценок (u₁, u₂):

(20, 225) ~ (40, 320) ~ (60, 390); (20, 100) ~ (40, 170) ~ (60,210).

Первая последовательность послужила основанием для построения кривой Q₁, а вторая – для нахождения Q₂.

Кривая безразличия Q₂ разделила множество S на подмножества S₁ = |u¹| и S₂ = |u², u³, u⁴|. Согласно проведенному выше анализу векторные оценки из S₁ явно предпочтительнее векторных оценок из S₂. Для того, чтобы упорядочить по предпочтительности оценки из S₂, необходимо построить интегральный критерий.

Прежде всего необходимо проверить, возможна ли аппроксимация _n(u) простейшими законами на основе Q-нормальной формы, для чего необходимо сопоставить графики на рис. 7.2 с кривыми Q₁ и Q₂ на рис. 7.3. Взаимное расположение Q₁ и Q₂ не может быть описано линейным, логарифмическим, показательным или степенным законом при k₁(u^(n-1)) = const. Следовательно, для построения интегрального критерия требуется больше двух поверхностей безразличия. Для точки b (рис. 7.3) ЛПР указал такие точки а и с, что а ~ b ~ с или (25, 190) ~ (40, 240) ~ (55, 280). Эта дополнительная информация позволяет проверить возможность использования того или иного закона аппроксимации функции _n(u) для случая k₁(u^(n-1)) = = const.

1. Для линейного закона согласно:

(b) = k₁(b₁)[b₂ – f₁(b₁)] + e₁;

.

Предположим, что e₁ = 0, е₂ = 1. Тогда из графиков Q₁ и Q₂ на рис. 7.3:

k₁(b₁) = l/[f₂(b₁) – f₁(b₁)] = l/(0,23–0,08) = 6,667;

(b) = 6,667 (0,16–0,08) = 0,533.

Из уравнения 0,533 = k₁(u₁)[u₂ – f₁(u₁)], где k₁(u₁) = 1/[f₂(u₁) – f₁(u₁)], можно получить уравнение u₂ = 0,533[f₂(u₁) – f₁(u₁)] + f₁(u₁) = 0,533f₂(u₁) + + 0,467f₁(u₁), определяющее кривую безразличия для линейного закона на рис. 7.3, соответствующую значению интегрального критерия е = 0,533.

2. Для логарифмического закона при e₁ = 0, е₂ = 1

_{(b) = k1(b1)[ln b2 – ln f1(b1)],}

где k₁(b₁) = 1/[ln f₂(b₁) – ln f₁(b₁)] = 1/(ln 0,23 – ln 0,08) = 0,947, и, следовательно, (b) = 0,947(ln 0,16 – ln 0,08) = 0,656.

Из уравнения 0,656 = [ln u₂ – ln f₁(u₁)]/[ln f₂(u_i) – ln f₁(u₁)] можно получить уравнение кривой безразличия и₂ = (f₂(u₁))^0,656 (f₁(u₁))^0,344 для логарифмического закона аппроксимации, построенной на рис. 7.3.

Рис. 7.3. Выбор закона аппроксимации функции _n(u)

3. Для показательного закона при e₁ = 0, е₂ = 1

k₁ (b₁) = 1/[ехр (f₂(b₁)) – exp (f₁(b₁))] = 1/(ехр 0,23 – ехр 0,08) = 5,704;

= k₁(b₁) [ехр (f₂(b₁)) – ехр (f₁(b₁))] = 5,704 (exp 0,16 – ехр 0,08) = 0,515, кривая безразличия u₂= ln [0,515ехр(f₂(u₁)) + 0,485ехр (f₁(u₁))] для показательного закона аппроксимации изображена на рис. 7.3.

4. Для степенного закона при K = 0,5

и кривая безразличия для степенного закона аппроксимации на рис. 7.3 описывается уравнением

.

Для проверки близости закона аппроксимации и кривой безразличия, определенной ЛПР, необходимо определить значения интегральных критериев для точек a и с:

1) линейный закон

u₂ = 0,533f₂(u₁) + 0,467f₁(u₁);

u₂(а) = 0,533  0,28 + 0,467  0,15 = 0,219;

u₂(b) = 0,160;

u₂(c) = 0,533  0,20 + 0,467  0,025 = 0,118.

(а) = 6,667(0,219–0,15) = 0,462;

(b) = 0,533

(c) = 6,667(0,219–0,15) = 0,622.

2) логарифмический закон

и₂ = (f₂(u₁))^0,656 (f₁(u₁))^0,344;

u₂(а) = 0,28^0,656  0,15^0,344 = 0,226;

u₂(b) = 0,160;

u₂(c) = 0,20^0,656  0,025^0,344 = 0,098.

(а) = 0,947(ln 0,226–ln 0,15) = 0,388;

(b) = 0,656

(c) = 0,947(ln 0,098–ln 0,025) = 1,292.

3) показательный закон

u₂= ln[0,515ехр(f₂(u₁)) + 0,485ехр(f₁(u₁))]

u₂(а) = ln(0,515 exp 0,28 + 0,485 exp 0,15) = 0,219;

u₂(b) = 0,160;

u₂(c) = ln(0,515 exp 0,20 + 0,485 exp 0,025) = 0,119.

(а) = 5,704(exp 0,219–ехр 0,15) = 0,473;

(b) = 0,515

(c) = 5,704(exp 0,119–ехр 0,025) = 0,576.

4) степенной закон

u₂(а) = = 0,223;

u₂(b) = 0,160;

u₂(c) = = 0,109.

(а) = 5,083 = 0,429;

(b) = 0,595

(c) = 5,083 = 0,875.

Ближе всего к кривой безразличия, которую можно провести через эквивалентные точки a, b и с, подходят кривые, соответствующие линейному и показательному законам аппроксимации функции (u), практически совпадающие на рис. 7.3. Проверка близости может быть проведена по min квадратичных отклонений

:

1) линейный закон:  = 0,114;

2) логарифмический закон:  = 0,346;

3) показательный закон:  = 0,074;

4) степенной закон:  = 0,325.

В качестве закона аппроксимации выбираем показательный закон и из рис. 7.3 имеем:

(u¹) = 5,704(exp 0,3 – exp 0,14) = 1,138;

(u²) = 5,704(exp 0,23 – exp 0,105) = 0,844;

(u³) = 5,704(exp 0,16 – exp 0,065) = 0,607;

(u⁴) = 5,704(exp 0,1 – exp 0,017) = 0,502.

Поскольку (u¹) > (u²) > (u³) > (u⁴), то u¹ u² u³ u⁴.

Задание

1. На основе эквивалентных последовательностей векторных оценок, выявленных ЛПР, провести линейную, логарифмическую, экспоненциальную, степенную аппроксимацию (u) на основе Q-нормальной формы.

2. Определить закон, наиболее точно описывающий (u).

3. Определить упорядочивание заданных векторных оценок.

Содержание отчета

1. Расчет линейной, логарифмической, экспоненциальной, степенной аппроксимации интегрального критерия на основе Q-нормальной формы.

2. Выбор закона, наиболее точно описывающего интегральный критерий.

3. Определение порядка предпочтительности альтернатив.

4. Графическое изображение результатов расчетов.

Вопросы

1. Q-нормальная форма интегрального критерия.

2. Методы аппроксимации.

3. Выбор закона аппроксимации.