Контрольні питання

1. Що таке кутова координата?

2. Визначення кутової швидкості.

3. Визначення кутового прискорення.

4. Яке прискорення зветься нормальним?

5. Яке прискорення зветься тангенціальним?

6. Який звязок між лінійною та кутовою швидкістю?

7. Який звязок між тангенціальним та кутовим прискоренням?

8. Визначення для моменту інерції твердого тіла.

9. Що таке момент сили?

10. Визначення моменту імпульсу твердого тіла та його звязок з кутовою швидкістю обертання.

Лабораторна робота № 4 Знаходження моменту інерції твердого тіла методом Гауса

Обладнання: крутильний маятник, лічильник часу, штангенциркуль, кільце з відомою масою; тіло довільної форми, момент інерції якого вимірюється.

Мета роботи: ознайомитись з одним із методів експериментального визначення моменту інерції твердого тіла – методом Гауса, або методом обертальних коливань, знайти момент інерції заданого тіла.

Теоретичні відомості та описання лабораторної установки

Крутильний маятник зображений на рисунку 1. Він складається з сталевої проволки 1 натягнутої між двома вертикальними затискачами А і В; посередині проволки закріплене тіло 3, момент інерції якого вимірюється; на тілі 3 знаходиться кільце 2, відомої маси.

А

2

1

3

В

Рис. 1

Крутильні або обертальні коливання в даній системі виникають внаслідок дії моменту пружних сил, який виникає при закручуванні сталевої проволки. Згідно закону Гука проекція моменту пружних сил на вісь обертання дорівнює:

(1)

де: - модуль кручення проволки; - малий кут кручення в радіанах.

З іншого боку, якщо знехтувати опором, то проекція моменту пружних сил, за основним законом динаміки обертального руху повинна дорівнювати:

(2)

де: - момент інерції тіла, закріпленого посередині проволки.

Прирівнюючи проекції моменту пружних сил із виразів (1) та (2) отримаємо диференціальне рівняння гармонічних коливань даної системи:

(3)

З рівняння (3) можна визначити циклічну частоту та період власних коливань для крутильного маятника:

(4)

оскільки, за визначенням , то: . (5)

Запровадимо такі позначення: - момент інерції тіла 3; - момент інерції кільця 2; - циклічна частота коливань маятника у випадку, коли посередині проволки закріплене тільки тіло 3; - період коливань маятника у випадку, коли посередині проволки закріплені тіло 3 і кільце 2 разом.

Згідно формулі (5) періоди коливань будуть дорівнювати:

; (6)

. (7)

Підводячи обидві частини рівнянь (6) та (7) до квадрату і розділивши одне рівняння на друге маємо:

. (8)

В даній лабораторній роботі, на досліді, ми будемо вимірювати час , за який тіло 3 здійснить рівно повних коливань і час , за який кільце 2 разом із тілом 3 здійснить таку ж само кількість повних коливань , тоді періоди коливань можна буде знайти таким чином:

. (9)

Підставляючи співвідношення (9) у вираз (8) отримаємо формулу для знаходження моменту інерції тіла 3:

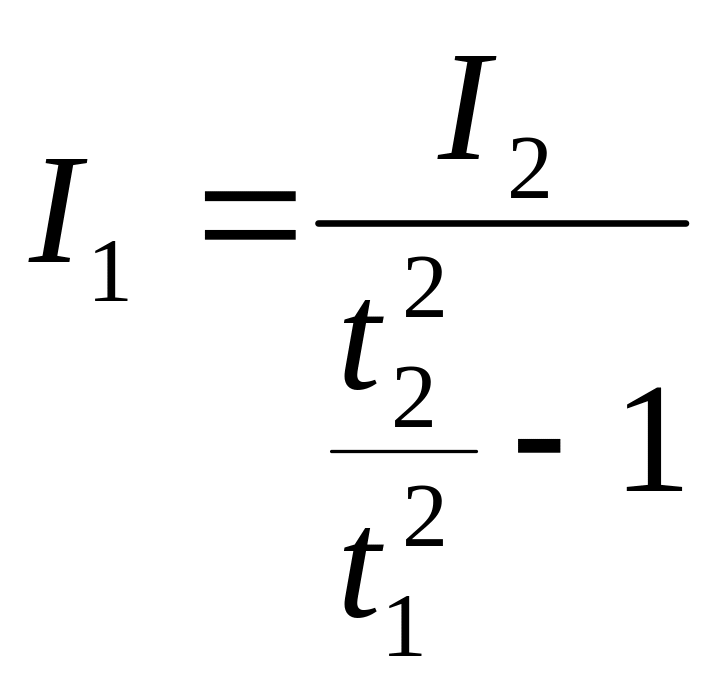. (10)

Використовуючи формулу (10) можна обчислити момент інерції тіла 3, якщо буде відомий момент інерції кільця . Виразимо момент інерції кільця , відносно його осі симетрії, через його масу , зовнішній радіус кільця та його внутрішній радіус .

Якщо розподіл мас у кільця неперервний, то його момент інерції, за визначенням, можна знайти як інтеграл:

, (11)

де: - маса частки кільця нескінчено малого об’єму ( під нескінчено

малою часткою треба розуміти кільце нескінчено малої ширини );

- відстань нескінчено малої частки кільця до осі обертання ( див. рис. 2).

Рис. 2.

Загальний об’єм кільця дорівнює:

, (12)

де: - товщина кільця, тоді середня густина кільця буде дорівнювати:

. (13)

Об’єм нескінчено малої частки кільця буде дорівнювати:

; (14)

тоді маса частки буде такою:

, тобто, . (15)

Підставляючи масу частки (15) в інтеграл (11), отримаємо момент інерції кільця:

. (16)

На досліді вимірюються зовнішній та внутрішній діаметри кільця 2, зв’язок між радіусами та діаметрами, звичайно, буде таким:

. (17)

Підставивши вирази (17) у співвідношення (16) одержимо:

. (18)