Способы описания движения тел

1. Координатный способ

Движение МТ в декартовой системе координат определяется тремя функциями, выражающими зависимость координат от времени (Рисунок 2).

Эта система уравнений называется законом движения (или уравнением движения).

Рисунок 3. Векторный способ описания движения МТ

Рисунок 2. Координатный способ описания движения МТ

2. Ве2

2. Векторный способ

Положение МТ в пространстве определяется в любой момент времени радиус – вектором , проведенным из начала координат до МТ (Рисунок 3).

Кинематические параметры МТ

М

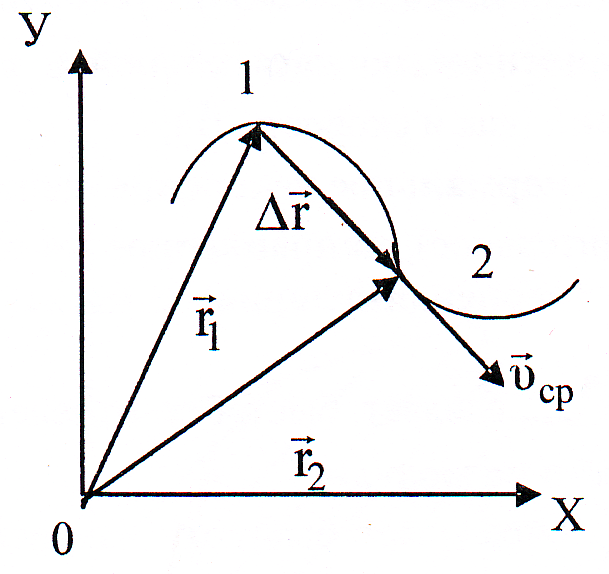
Т обладает следующими кинематическими параметрами: перемещением, скоростью (средней и мгновенной) и ускорением (средним и мгновенным). За малый промежуток времени t МТ совершит малое перемещение из точки 1 в точку 2: (Рисунок 4).

Средняя скорость движения за время t определяется соотношением

= .

Направление средней скорости совпадает с направлением .

Рисунок 2. Скорость движения МТ

Мгновенная скорость — это предел, к которому стремится средняя скорость за бесконечно малый промежуток времени. — называется производной от перемещения по времени или дифференциалом функции перемещения.

М

Вектор мгновенной скорости в любой точке траектории

направлен по касательной к траектории в этой точке

Вектор мгновенной скорости в любой точке траектории

направлен по касательной к траектории в этой точке

Вектор мгновенной скорости в любой точке траектории

направлен по касательной к траектории в этой точке

Вектор мгновенной скорости в любой точке траектории

направлен по касательной к траектории в этой точке

одуль скорости:

Ускорение

Скорость тела может меняться как по модулю, так и по направлению. Изменение скорости характеризуется ускорением.

Среднее ускорение:

М гновенное ускорение: ;

Вектор мгновенного ускорения при криволинейном движении обычно представляют в виде векторной суммы двух ускорений (Рисунок 3).

- тангенциальное ускорение, направленное по касательной к траектории (как и скорость ), определяет быстроту изменения скорости по модулю;

Рисунок 3. Ускорение МТ

- нормальное ускорение (центростремительное), направленное по нормали (перпендикулярно) к касательной, определяет быстроту изменения скорости по направлению.

и перпендикулярны друг другу, поэтому модуль полного ускорения

Контрольные вопросы:

1. Что такое механика и чем она занимается?

2. Что такое кинематика?

3. Расскажите о системе отсчета МТ и о траектории.

4. Какие способы описания движения тел вы знаете?

5. Как вычисляется средняя скорость?

6. Как определить модуль и направление мгновенной скорости?

7. Что такое среднее ускорение и мгновенное ускорение?

8. На какие составляющие можно разложить ускорение при криволинейном движении?

Движение мт по прямой и по окружности

В случае прямолинейного движения МТ ускорение .

При равномерном прямолинейном движении МТ вдоль координаты ( , ) модуль скорости: . Здесь - координата МТ в начальный момент времени. Эту координату называют начальным условием. Если отсчет времени начинается от 0 ( ), то . Отсюда координата МТ в момент : .

В общем случае модуль перемещения МТ к моменту времени : .

Для двухмерного пространства ХОY и прямолинейного равномерного движения МТ координаты МТ в любой момент времени вычисляются по формулам:

, где и - начальные условия (координаты МТ при времени );

- проекции вектора скорости на оси и ;

При равноускоренном прямолинейном движении МТ в двухмерном пространстве (при ) и начальных условиях: , , , проекции скорости на координаты и :

;

.

Рисунок 4. График пройденного пути

Площадь под графиком (Рисунок 4), численно равная пройденному пути, является площадью трапеции:

.

Учитывая, что получим, что перемещение при равнопеременном движении: .

Перемещение может быть вычислено и по формуле: .

Координаты МТ в двухмерном пространстве вычисляются по формулам:

; .

Движение МТ по окружности с постоянной по модулю скоростью

При равномерном движении МТ по окружности (рисунок 7) радиус-вектор описывает за равные промежутки времени t равные углы .

Рисунок 5. Движение МТ по окружности

Отношение называется средней угловой скоростью.. При равномерном движении МТ по окружности =const и . Размерность угловой скорости: .

Пусть радиус-вектор совершит один полный оборот, т.е. повернется на угол Dj = 2 за время Dt = Т. Время Т одного полного оборота МТ называется периодом вращения. Таким образом: , где:

Частота вращения - это число оборотов в 1 секунду. Размерность частоты - (герц)

Один Герц – это частота, при которой МТ совершает один полный оборот за 1 секунду.

Угол поворота в радианах , где - длина дуги, а - радиус окружности.

Модуль линейной скорости МТ, вращающейся по окружности с радиусом , равен производной от длины дуги по времени: . Т.к. , то .

Т

аким образом,

Рисунок 6. Ускорение МТ при ее движении по окружности

Ускорение МТ при равномерном движении по окружности (Рисунок 8) можно определить следующим образом:

так как модуль скорости не меняется, то ускорение меняет только направление вектора скорости, т.е. является нормальным

АВС - равнобедренный. Угол между и в пределе стремится к , а ускорение направлено к центру окружности. Из подобия треугольников ОАD и АВС следует: .

При малом времени t длина дуги DS мало отличается от .

Модуль среднего ускорения : .

Модуль мгновенного ускорения:

.

В этом выражении v – частота вращения.