Приклад 4. Знайдемо . Оскільки і , то , , .

8. Степінь з довільним показником. За означенням

.

Зокрема, .Таким чином, , але не збігається з . Надалі, якщо не вказано на інше, під будемо розуміти .

Приклад 1. .

9. Синус і арксинус комплексного числа. За означенням для довільного комплексного числа z

. (1)

Ця рівність визначає для довільного комплексного числа . Якщо , то з формул Ейлера , отримуємо, що права частина (1) дорівнює , де – те, що під цим символом розуміється в дійсному аналізі. Арксинусом комплексного числа z називається таке число w, для якого , і позначається через . Для знаходження w маємо рівняння

,

звідки . Отож, остання формула задає всі розв’язки рівняння . Тому,

.

Якщо , і , то

, (2)

тобто в даному випадку , . Із рівності (2) отримуємо, що , , тобто тоді і тільки тоді, коли для деякого . Отож, при переході у комплексну площину в рівнянні не з’являється нових коренів.

Гіперболічним синусом комплексного числа називається комплексне число

.

Із означення випливає, що .

Приклад 1.

, , .

Приклад 2. і тому нерівність для комплексних чисел z не обов’язково виконується ( може бути більшим від наперед заданого числа ).

Приклад 3. Запишемо комплексне число в алгебраїчній, тригонометричній та показниковій формах. Маємо

,

, .

Отже,

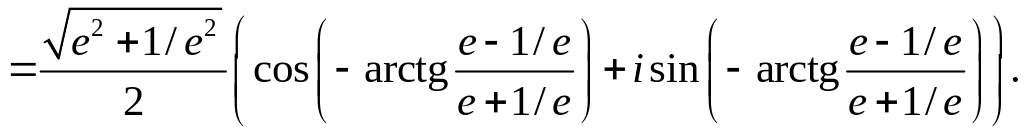
10. Косинус і арккосинус комплексного числа. Косинусом комплексного числа z зветься число

.

З формули Ейлера випливає, що для дійсних z це означення збігається із введеним в дійсному аналізі, а також, що . Арккосинусом комплексного числа називається таке число , яке є розв’язком рівняння . Множина всіх розв’язків рівняння позначається через . Для знаходження маємо рівняння

,

з якого знаходимо, що , тобто

.

Якщо , і , то i

.

Отож, , , . Зокрема, , . Отже, при переході в множину комплексних чисел у рівнянні нових коренів не з’являється. Водночас,

і тому нерівність для комплексних не обов’язково виконується.

Гіперболічним косинусом комплексного числа називається комплексне число

.

Із означення випливає, що .

Приклад 1. Знайдемо . Маємо

.

11. Тангенс, котангенс, арктангенс та арккотангенс комплексного числа. Тангенсом і котангенсом комплексного числа називаються відповідно числа

, .

Множина розв’язків рівняння позначається через , а кожний елемент w цієї множини називається арктангенсом числа z. Для знаходження кожного числа маємо рівняння

,

з якого знаходимо, що

,

Якщо , то звідси отримуємо , .

Множина розв’язків рівняння позначається , а кожний елемент цієї множини називається арккотангенсом комплексного числа . Для знаходження маємо рівняння

з якого знаходимо, що

.

Якщо , то , .

Числа

,

називаються відповідно гіперболічним тангенсом і гіперболічним котангенсом комплексного числа . Із означення випливає, що , . Всі тригонометричні формули залишаються справедливими і в . Наприклад,

, ,

, .

Ці формули доводяться на основі означень.

Приклад 1.

.

12. Відповідність. Відповідністю з множини в множину називається будь-яка сукупність упорядкованих пар , де , а . Іншими словами, відповідність з множини в множину – це будь-яка підмножина декартового добутку . Відповідність позначається так: або . Кожна упорядкована пара називається точкою відповідності , –образом елемента , а – прообразом елемента w. При цьому кажуть, що елемент w відповідає елементу . Множина всіх образів елемента позначається через , а множина всіх прообразів елемента – через . Сукупність тих елементів множини , яким відповідає хоч-би один елемент множини називається множиною (областю) визначення відповідності і позначається через , а сукупність тих елементів множини , які відповідають хоч-би одному елементу множини називається множиною значень відповідності і позначається символом . Символом позначають повний образ множини , тобто сукупність всіх тих елементів w множини , для яких існує хоч-би один елемент множини , образом якого є . Символом – позначають повний прообраз множини , тобто сукупність тих елементів z множини , яким відповідає хоч-би один елемент . Якщо – відповідність і , то кажуть, що відображає на . Якщо , то кажуть, що відповідність є відповідністю в . Відповідність можна задати різними способами (формулою, описом і т.д.).

Приклад 1. Множина є відповідністю в .

Приклад 2. Множина є відповідністю в .

Приклад 3. Кожна із формул , , , задає деяку відповідність в , тобто деяку множину упорядкованих пар .

13. Функції. Функцією з множини в множину називається така відповідність , за якої кожному елементу відповідає не більше одного елемента . Замість терміну “функція” вживаються також терміни “оператор”, “відображення”, “перетворення” і так далі. Коли говорять про функцію, то часто додають слово “однозначна”, тобто говорять “однозначна функція”. Цим підкреслюють, що жодному елементу не відповідає більше одного елемента множини . Багатозначною або многозначною функцією з в називається така відповідність , за якої принаймні одному елементу множини відповідає більше, ніж один елемент множини . За такого означення багатозначної функції, функція (однозначна) не є багатозначною функцією. Інколи функції (однозначні) також відносять до багатозначних. Тоді багатозначна функція – це будь-яка відповідність із множини в . Отож, термін “багатозначна функція” вживається в двох контекстах (частіше в другому). Це не призводить до непорозумінь, бо з тексту завжди зрозуміло, що мається на увазі. Говорячи про функцію ми не припускаємо, що , тобто включення може бути строгим. Якщо , то кажуть, що функція є функцією в . Функція називається оборотною або однолистою, якщо різним відповідають різні , тобто якщо з рівності випливає, що . Якщо – оборотна функція, то оберненою до неї називається така функція , для якої і образом елемента є такий елемент , що . Якщо функція не є оборотною, то вона не має оберненої функції, але вона має багатозначну обернену функцію. Багатозначною оберненою функцією до функції називається така багатозначна функція , для якої і образом кожного елемента є всі ті елементи , для яких . Функції комплексної змінної мають, як правило, тільки багатозначні обернені функції. Наприклад, багатозначні функції , , i є багатозначними оберненими до однозначних, але не однолистих функцій , , та , відповідно. Звуженням функції на множину називається така функція , для якої для всіх . Продовженням функції на множину називається така функція , для якої для всіх . Якщо функція є продовженням функції на множину , то функція є звуженням функції на множину і навпаки. Однозначною гілкою багатозначної функції називається така функція (однозначна) , для якої і для всіх виконується . Сумою, добутком і часткою двох багатозначних функцій та називаються такі багатозначні функції , та , множина визначення кожної з яких є перетином множин визначення функцій та , а образом кожного є відповідно множини , та .

Приклад 1. Відповідність не є функцією в .

Приклад 2.Формула задає функцію в .

Приклад 3. Відповідність, визначена формулою , не є функцією в .

Приклад 4. Багатозначна функція є продовженням функції з на .

Приклад 5. Функції і є однозначними гілками багатозначної функції , а функції

, ,

, ,

, ,

є однозначними гілками багатозначної (двозначної) функції _.

Приклад 6. Якщо , то , .

14. Відкриті і замкнені множини. -околом точки називається множина . -околом (нескінченності) називається множина . Проколеним -околом точки називається множина . Множина називається відкритою, якщо кожна її точка належить разом із деяким своїм околом. Множина називається замкненою в , якщо множина є відкритою. Точка називається межовою точкою множини , якщо будь-який її -окіл містить як точки, які належать так і точки, які не належать . Сукупність всіх межових точок множини називається її межею і позначається через . Множина називається замиканням множини . Замикання будь-якої множини є замкненою множиною. Компактами в , як і в , є обмежені замкнені множини і тільки вони. Тому із кожного відкритого покриття обмеженої замкненої множини множини можна виділити скінчене підпокриття. При цьому множина називається обмеженою в , якщо . Якщо множини і є замкненими, мають порожній перетин і принаймні одна з них є обмеженою, то , де – відстань між множинами і . Це випливає безпосередньо із означень. Далі ми будемо використовувати наступні позначення.

1. – відкритий круг з центром в точці і радіусом .

2. – замкнений круг з центром в точці і радіусом .

3. – коло з центром в точці і радіуса . Рівняння цього кола можна записати так: , .

4. , , , – відповідно права, верхня, ліва, нижня півплощини.

5. , – кут з вершиною в точці нуль, який обмежений променями i .

15. Границя послідовності. Послідовністю в називається така функція , для якої є множиною визначення. Оскільки можна подати у вигляді , де , а , то задання послідовності в рівносильне задаванню двох послідовностей і в . Число називається границею послідовності , якщо для кожного знайдеться таке , що всі члени послідовності , для яких , належить . У випадку це означення можна сформулювати так: число називається границею послідовності , якщо

_{. (1)}

У випадку це означення можна сформулювати так: число називається границею послідовності , якщо

. (2)

Послідовність, яка має границю , називається збіжною в . Послідовність, яка має границю називається збіжною в .

Теорема 1. Для того щоб послідовність була збіжною і мала своєю границею число , необхідно і достатньо, щоб збіжними в були послідовності та і мали границі та , відповідно, тобто

, (3)

якщо останні дві границі існують. Для того щоб число було границею послідовності , необхідно і достатньо, щоб принаймні одна з границь

, (4)

дорівнювала в . Для того щоб число було границею в послідовності , , необхідно і достатньо, щоб числа та були границями в послідовностей та , відповідно, тобто , якщо існує границя в лівій частині цієї рівності або існують обидві границі в її правій частині.

Доведення. Перша частина цієї теореми випливає із нерівностей

а друга – безпосередньо з означень. ►

Теорема 2. Для того щоб послідовність була збіжною в , необхідно і достатньо, щоб

_.

Теорема 3. Для кожної обмеженої послідовності існує збіжна в її підпослідовність. Для кожної послідовності існує збіжна в її підпослідовність.

Доведення. Теореми 2 і 3 отримують з теореми 1 і відповідних теорем для дійсних послідовностей. При цьому послідовність називається обмеженою в , якщо . ►

Наслідок 1. Множина з відстанню є повним метричним простором.

Основні теореми про границю суми, добутку та частки справедливі і для комплексних послідовностей.

Приклад 1.

.

Приклад 2. Для існування границі

, (5)

необхідно і достатньо, щоб

, (6)

і для деякого , а тому і для кожного, існувала послідовність , для якої

. (7)

Справді, якщо виконується (6) і (7), то

.

Навпаки, якщо виконується (6), то із нерівності та означення границі випливає (7). Далі, для великих . Тому для заданих та знайдеться , для якого . Звідси випливає (7). Водночас, безпосередньо з означення границі випливає, що тоді і тільки тоді, коли .

Зауваження 1. Послідовністю в називається така функція , для якої є множиною визначення. Інколи зручно називати послідовністю в довільну функцію . У випадку такого означення множина визначення послідовності може бути і скінченною (випадок не виключається). Послідовність, для якої є множиною визначення, називають, інколи, нескінченною послідовністю, а послідовність, множина визначення якої є скінченною, – скінченною послідовністю. Про скінченні послідовності доцільно говорити при вивченні послідовностей нулів функцій та інших питань.

16. Числові ряди. Нехай – послідовність комплексних чисел,

. (1)

Ряд

називається збіжним в (в ), якщо існує границя

. (2)

При цьому число S називається сумою ряду (1) і цей факт записують так

. (3)

Ряд (1) називається абсолютно збіжним, якщо збіжним в є ряд

.

Теорема 1. Якщо ряд (1) є збіжним, то його загальний член прямує до нуля: .

Теорема 2. Для того щоб ряд (1) був збіжним в і мав суму , необхідно і достатньо, щоб були збіжними в ряди

і , (4)

і мали суми та відповідно.

Теорема 3. Для того щоб ряд (1) був збіжним в , необхідно і достатньо, щоб

. (5)

Теорема 4. Якщо ряд (1) є абсолютно збіжним, то він є збіжним в .

Теореми 2 і 3 випливають з відповідних теорем для послідовностей, а теорему 4 отримують на основі теореми 2 так само, як відповідну теорему для дійсних числових рядів. Теорема 1 випливає з рівності .

Наслідок 1. Якщо , то ряд (1) є збіжним абсолютно. Якщо ж , то ряд (1) розбіжний.

Наслідок 2. Якщо , то ряд (1) є збіжним абсолютно. Якщо ж , то ряд (1) є розбіжним.

Добутком ряду (1) і ряду

(6)

називається такий ряд

, , (7)

члени якого утворюються із все можливих добутків .

Теорема 5. Якщо абсолютно збіжними є ряди (1) та (7) і мають суми S і відповідно, то збіжним абсолютно є також їх добуток і має суму S , причому

Доведення цієї теореми таке ж як і її аналогу для дійсних рядів.

Приклад 1. Оскільки ряд є розбіжним, то ряд також є розбіжним.

Приклад 2. Оскільки і ряд є збіжним, то ряд є збіжним абсолютно.

_{Приклад 3. Розглянемо ряд}

.

Оскільки

,

то цей ряд є розбіжним, якщо , і є збіжним та має суму , якщо Отже, ,

_{Приклад 4. Знайдемо суму}

.

Маємо

.

17. Функції з в . Функцією з в називається така функція , для якої і . Кожну таку функцію можна подати у вигляді , де і . Тому задання функції рівносильне задаванню функції . Число називається границею функції в точці , якщо

.

Функція називається неперервною в точці , якщо

.

Похідною функції в точці називається границя

.

Теорема 1. Для того щоб число було границею функції в точці , необхідно і достатньо, щоб i , тобто

,

якщо останні дві границі існують. Для того щоб функція була неперервною в точці , необхідно і достатньо, щоб в цій точці були неперервними функції і , як функції із в . Для того щоб функція мала похідну в точці , необхідно і достатньо, щоб функції і як функції з в , мали похідну в точці . Якщо остання умова виконана, то .

Доведення. Перша частина цієї теореми випливає з нерівностей , а решта є наслідком першого. ►

Клас функцій, які мають на проміжку неперервні похідні до порядку включно, позначатимемо через . При цьому – клас функцій, неперервних на . Якщо проміжок є замкненим, то під похідною на кінцях проміжку розуміються відповідні однобічні похідні.

18. Шлях і рівняння його дотичної. Шлях в задається функцією , , а також параметрично системою

.

При цьому і . Якщо функція має похідну в точці , то в точці шлях має дотичну, рівняння якої має вигляд , . В параметричній формі рівняння дотичної записується так:

Тому кожне число дорівнює одному з кутів, утворених дотичною та вектором . Шлях це не тільки множина точок, але й порядок їх проходження, який задається функцією . При написанні рівняння шляху, можна вважати, що проміжком є проміжок , чим ми будемо часто користуватися. Точка шляху – це упорядкована пара , де . Ми будемо точку шляху позначати часто однією буквою , хоч таке позначення є природним лише у випадку, коли шлях не має точок самоперетину.

Приклад 1. Шляхи

1) , ; 3) , ;

2) , ; 4) , ;

задають коло. Проте тільки шляхи 1) і 3) можна вважати однаковими.

19. Шлях і крива. Шляхом в області називається будь-яка функція , де і . Шлях називається неперервним, якщо є неперервною функцією на і не існує проміжку , , на якому  є сталою (останню умову інколи не включають в означення неперервного шляху). Шлях називається гладким або регулярним, якщо він є неперервним і в кожній точці функція має похідну , причому є неперервною функцією на . Гладкий шлях в кожній точці має дотичну. Шлях називається кусково-гладким, якщо він є неперервним, існують точки , , такі, що і звуження на кожний проміжок , , є гладким шляхом. Точка називається початком шляху, а точка – його кінцем. Коло – це гладкий шлях, а ламана – кусково-гладкий. Шлях називається замкненим, якщо його початок збігається з його кінцем, тобто якщо . Шлях , , називається протилежним до шляху . Множина називається носієм шляху . При цьому, і можна сказати, що порядок проходження точок шляху є протилежним до проходження точок шляху : початок збігається з кінцем шляху і навпаки. Шлях називається жордановим, якщо він є неперервним і відображення є бієктивним (взаємнооднозначним). Жордановий шлях не має точок самоперетину. Шлях називається замкненим жордановим шляхом, якщо він є неперервним замкненим і різним з відповідають різні значення . Замкнений жордановий шлях не є жордановим шляхом. Надалі ми розглядатимемо тільки неперервні шляхи. Об’єднанням або добутком шляхів і називається шлях такий, що звуження на є шлях , а звуження на є шлях . Кривою в називається така множина, яка є носієм деякого шляху. Якщо крива є носієм шляху , то рівняння , , називається її параметризацією, а проміжок – множиною параметрів. Одна і та ж крива може бути носієм багатьох шляхів. Орієнтовною кривою називається упорядкована пара множини і одного з шляхів , носієм якого є . При цьому кажуть, що шлях  задає орієнтацію кривої . Вважають, що шляхи і задають однакову орієнтацію кривої , якщо існує зростаюча і неперервна на функція така, що і . При цьому кажуть, що шлях отримують із шляху заміною параметрів. Орієнтовна неперервна крива – це те спільне, що мають всі неперервні шляхи з однаковим носієм і однаковим порядком проходження точок. Із шляхів 1) – 4) тільки шляхи 1) і 3) є еквівалентними, і, отже, породжують одну і ту ж орієнтовну криву. Крива (орієнтовна крива) називається спрямованою, гладкою і т. д., якщо вона породжена відповідним шляхом. При цьому означення спрямованого шляху дається так само як і в дійсному аналізі.

Приклад 1. Пряма , , як і будь-яка інша пряма, не є неперервним шляхом в . Разом з цим, пряма , , як і будь-яка інша пряма, є неперервним шляхом в , де і , є неперервним шляхом в .

20. Область. Областю називається відкрита зв’язна множина. Відкрита множина є зв’язною тоді і тільки тоді, коли вона є лінійно зв’язною. Тому область – це відкрита множина , будь-які дві точки якої можна з’єднати неперервним шляхом , який лежить в . Оскільки множина неперервних шляхів є компактом, то будь-які дві точки області можна з’єднати ламаною, яка складається з скінченного числа відрізків і цілком лежить в . Область називається однозв’язною, якщо її межа є зв’язною множиною. Іншими словами, область називається однозв’язною, якщо внутрішність будь-якої замкненої жорданової кривої, що лежить в , також належить . Компонентою множини називається будь-яка найбільша зв’язна підмножина (тобто така підмножина, яка не належить жодній іншій зв’язній підмножині) множини. Кількість компонент межі області називається порядком зв’язності області. Кожна замкнена жорданова крива в ділить на дві області ( та – та що містить ) спільною межею, яких вона є. Замкненою областю називається така множина , для якої множина , є областю. Для кожної області існує послідовність замкнених обмежених областей таких, що

, ,

причому, якщо – однозв’язна, то і – однозв’язні області. Області можна побудувати у вигляді об’єднання скінченної кількості квадратів із сторонами паралельними осям координат. Для великих можна також взяти .

Приклад 1. Круг, півплощина – однозв’язні області, а кільце – двозв’язна область. Множина є нескінченнозв’язною областю.

Приклад 2. Можна побудувати область таку, що задану точку не можна з’єднати з деякою точкою неперервною кривою , яка лежить в . Так буде, наприклад, якщо

Приклад 3. Існують незліченнозв’язнні області. Наприклад, такою є область , де – канторова множина.

Зауваження 1. Межа області – це множина . При знаходженні інтегралів під ми будемо розуміти орієнтовну межу. Якщо область є обмеженою і однозв’язною, то орієнтовна межа – це замкнений шлях , який є параметризацією , причому такий, що якщо точка t рухається по від до , то точка рухається по так, що лежить зліва від спостерігача, який рухається по разом з і, крім цього, звуження на жодний проміжок не є такою параметризацією . Таку параметризацію будемо називати додатною.

Приклад 4. Якщо , то , а орієнтовною межею є шлях визначений так:

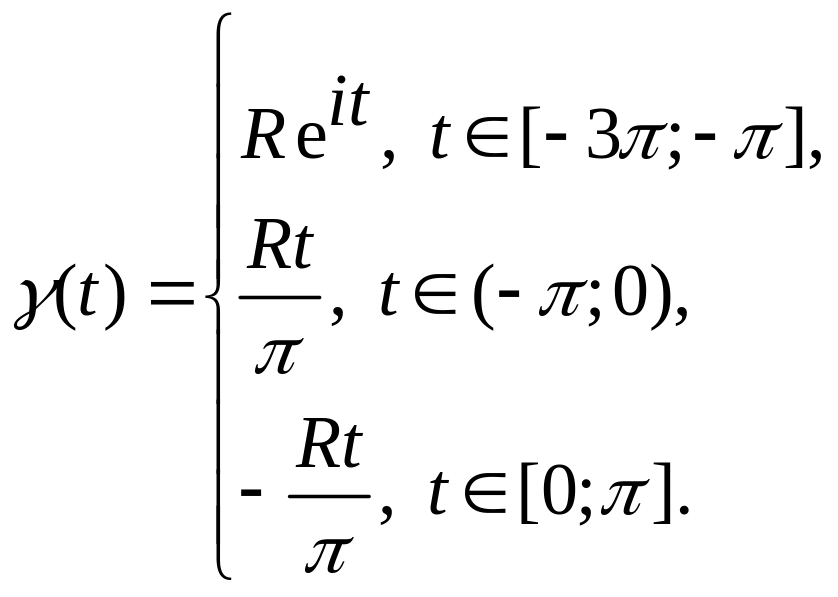
При цьому шлях , , називають нижнім берегом розрізу круга , а шлях , , – верхнім. Якщо область не є однозв’язною, а її межа є об’єднанням компонент , то під орієнтовною межею D розуміємо об’єднання замкнених шляхів , кожний з яких є параметризацією і володіє вказаними вище властивостями.

Приклад 5. Якщо , то орієнтовна межа D є об’єднанням шляхів , , і

21. Ще один погляд на криву. Інколи на криву дивляться інакше. Кривою в області називають зв’язну множину , кожна точка якої має окіл такий, що існує взаємно однозначна і взаємно неперервна відповідність між і однією із множин або . Ті точки із , для яких вказана відповідність існує між і називаються крайовими. Крива називається замкненою, якщо вона не має крайових точок і є замкненою множиною. Крива, яка не є замкненою називається незамкненою. Крива називається орієнтовною, якщо на ній задано орієнтацію. Орієнтацію задають вказуючи порядок проходження точок за допомогою вказування на кривій трьох (двох для незамкнених: початку і кінця), параметризації, напрямку одиничного вектора дотичної, напрямку одиничного вектора нормалі або якимсь іншим чином. При цьому природним чином вводиться поняття протилежно орієнтовної кривої . Криві в розглядуваному зараз розумінні є досить простими об’єктами: не мають точок самоперетину. За допомогою скінченної кількості таких орієнтовних кривих утворюються складніші об’єкти , які називають ланцюгом орієнтовних кривих. Ланцюг орієнтовних кривих, приблизно кажучи, є об’єднання множин з врахуванням їх орієнтації, причому якщо в ланцюгу є дві протилежно орієнтовні криві, то вони взаємно знищуються і отриманий після їх викидання новий ланцюг вважається рівним попередньому.

Приклад 1. Коло, пряма в – замкнені криві.

Приклад 2. Пряма в – незамкнена крива, яка не має крайових точок.

Приклад 3. Скінченний проміжок – незамкнена крива, яка має дві крайові точки та .

Приклад 4. Межа кільця є ланцюгом кіл та . Орієнтовна межа області , зображеної на малюнку 1 попереднього пункту, є ланцюгом кривих та , де , , а

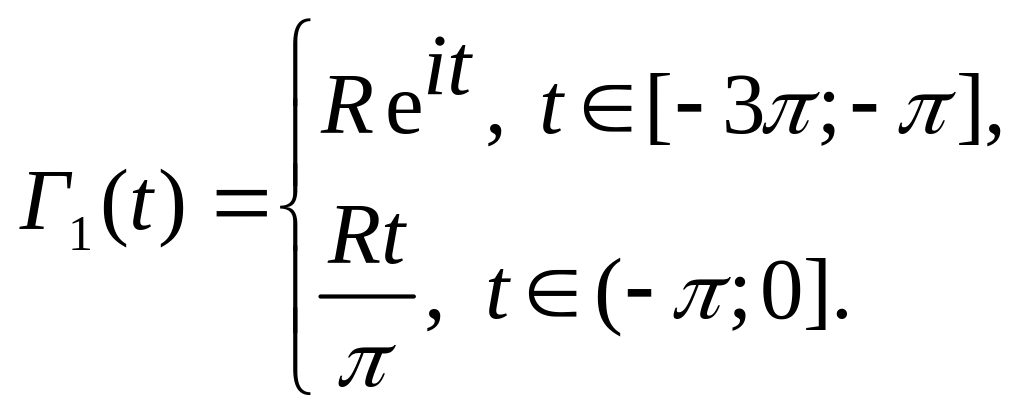
Приклад 5. Якщо , , то .

Зауваження 1. Є певні труднощі з означенням кривої. Ці труднощі пов’язані з тим, що зустрічаються криві, які мають точки самоперетину, а також не є зв’язними множинами. Крім наведених вище є і інші означення кривої. Тому в кожній конкретній ситуації потрібно добре задумуватись, що вкладається в терміни “крива” і ”шлях”.

22. Границя і неперервність функцій з в . Функція – це така функція, для якої і . Функція називається дійсною частиною, а функція – уявною частиною функції . Тому задавання функції рівносильне задаванню двох функцій i . Число називається границею функції в точці , якщо

.

Функція називається неперервною в точці , якщо .

Теорема 1. Для того щоб , , необхідно і достатньо, щоб

, .

Доведення. Теорема 1 випливає із нерівностей

.

Теорема 2. Для того щоб функція f була неперервною в точці , необхідно і достатньо, щоб функції u і v, як функції із в , були неперервними в точці (а₁; а₂).

Доведення. Ця теорема є наслідком теореми 1. ►

Як і в кожному метричному просторі функція є неперервною в області тоді і тільки тоді, коли прообразом кожної відкритої множини є відкрита множина.

Як і в курсі математичного аналізу дається означення границі функції за множиною :

.

Число називається границею функції в точці за множиною , якщо

.

Функція f називається неперервною на множині , якщо

.

Функція f називається рівномірно неперервною на множині , якщо

.

Теорема 3(Кантора). Якщо функція є неперервною на контакті , то вона є рівномірно неперервною на .

Доведення. Ця теорема випливає безпосередньо із теореми 2 і відповідної теореми для функції двох змінних. ►

Інколи ми будемо розглядати функції . Тоді означення границі потрібно відповідним чином змінити, сформулювавши його на мові околів.

Зобразити геометрично графік функції важко, оскільки потрібно чотири осі координат. Як правило поступають так. Беруть дві площини: z-площину і -площину. У z-площині зображають прообрази, а в -площині образи відповідних множин. Наприклад, якщо , то образом круга буде круг .

Рис. 1

Приклад 1. Покажемо, що

.

Справді,

.

Для фіксованого і великих точка лежить у правій півплощині, і

.

Але

.

Залишилось звернути увагу на приклад 2 пункту 15.

Приклад 2. Функція є неперервною в області . Це випливає з рівності

, де .

Зауваження 1. В комплексному аналізі розглядають загальніше поняття, ніж неперервність функції в замкненій області. Відстанню Мазуркевича між точками і області називається число , яке дорівнює точній нижній межі довжин ламаних, які з’єднують ці точки і лежать в . Функція називається неперервною в аж до межі, якщо

. (1)

Кожна рівномірно неперервна в функція задовольняє умову (1). Кожна неперервна в функція є рівномірно неперервною в і тому також задовольняє умову (1). Якщо складається із скінченної кількості замкнених жорданових кривих, то умова (1) рівносильна рівномірній неперервності в . Для областей з розрізами, неперервність аж до межі є загальнішим поняттям, ніж неперервність в замкненій області. Якщо межа області складається зі скінченної кількості жорданових кусково-гладких кривих і функція є неперервною в аж до межі, то область можна розбити на скінченне число областей так, що звуження на кожну область можна продовжити до функції неперервної . Якщо для функції область можна таким чином розбити, то говоримо, що функція є неперервною в замкненій області з орієнтовною межею.

Приклад 3. Функція , , розглядувана в області , є неперервною в , але не є неперервною в , бо коли залишаючись у верхньому півкрузі, то , а коли залишаючись у нижньому півкрузі, то . Ця функція стає неперервною в з орієнтовною межею, якщо під на верхньому березі розрізу розуміти , а на нижньому – . Такий підхід природний, бо так продовжена функція є неперервною в замкнених областях і , де , .