Розділ 6

Розділ 6. Аналітичне продовження і аналітичні функції

1. Поняття голоморфного продовження. Голоморфним продовженням функції з множини в область називається така голоморфна в функція , що . Якщо множина має граничну точку , то за теоремою єдиності голоморфне продовження єдине, якщо воно існує. Якщо функція є голоморфною в області і не існує голоморфного продовження в жодну область , , то кажуть, що є природною областю голоморфності, а є природною межею голоморфності функції . Якщо функція задана деякою формулою, то часто для знаходження голоморфного продовження досить задати іншою формулою, яка має зміст на ширшій множині, ніж . Узагальненням поняття голоморфного продовження є аналітичне продовження, яке розглядається далі.

Приклад 1. Функції є голоморфними продовженнями в відповідних функцій, розглядуваних в .

Приклад 2. Функція є голоморфною в , але ряд

є збіжним при всіх . Отже, є голоморфним продовженням із множини Е в .

Приклад 3. Функція

є голоморфною в . Але

і є голоморфною в . Тому є голоморфним продовженням з в .

Приклад 4. Функція

, ,

є голоморфною в півплощині , оскільки останній інтеграл рівномірно збігається на кожному компакті з цієї півплощини. Але в розглядуваній півплощині

. (1)

Перший доданок правої частини формули (1) є голоморфною функцією в області , другий є голоморфною функцією в півплощині , а останній є цілою функцією. Отож, права частина (1) є функцією голоморфною в області і задає голоморфне продовження функції в цю область. Оскільки можна брати будь-яким, то приходимо до висновку, що функція допускає аналітичне продовження в область .

Приклад 5. Розглянемо функцію

Ця функція голоморфна в крузі і , якщо бо , . Але . Тому , якщо . Аналогічно, і тому Але в будь-якому колі кожної точки є нескінченно багато точок виду . Тому функцію не можна голоморфно продовжити в жодну область D, яка містить і .

Приклад 6. Нехай

, (2)

, (3)

. (4)

Функція є голоморфною в і її значення належать , є взаємно-однозначним відображенням на і , тобто . Формула ( 1 ) визначає і для , але так визначена функція не є неперервною як функція з в і , тим більше, голоморфною в точках від’ємного дійсного променя. Водночас, функція є голоморфною в області і для всіх маємо . З іншого боку , функція є голоморфною в області і для всіх виконується . Безпосередньо з означення випливає, що . Отож, голоморфним продовженням в звуження на є функція , а голоморфним продовженням в звуження на є функція . Водночас, . Цей приклад показує, що хоч функція не допускає голоморфного продовження в , але її звуження допускає і результат голоморфного продовження залежить від множини, на якій розглядають звуження. Тому доцільного розглянути загальніше поняття, ніж поняття голоморфного продовження.

2. Безпосереднє аналітичне продовження. Аналітичним елементом або елементом називається упорядкована пара області D і голоморфної в D функції f. Елемент називається безпосереднім аналітичним продовженням елемента через область , якщо і . При цьому називається результатом аналітичного продовження. Кажуть, що є безпосереднім аналітичним продовженням через точку , якщо існує область така, що і є безпосереднім аналітичним продовженням через . Функція

не обов’язково, як показує останній приклад, є голоморфною в області , бо в цій області F може бути багатозначною, оскільки і крім можуть мати і інші спільні області.

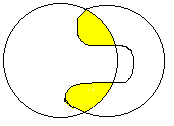
Рис.1

Проте, якщо і є кругами або будь-якими іншими опуклими областями, то є областю і F є голоморфною в і в такому випадку F є аналітичним продовженням із в .

Елемент називається аналітичним продовженням елемента вздовж ланцюга канонічних елементів або через області , , якщо для кожного k елемент є безпосереднім аналітичним продовженням елемента через область .

Теорема 1. Якщо елементи і є безпосереднім аналітичним продовженням елемента через область , то .

Доведення. Ця теорема є іншим формулюванням теореми єдиності. ►

Приклад 1. Нехай

,

.

Функції і є голоморфними в і відображають взаємно-однозначно на області і . Крім цього, ( ): , тобто вони є оберненими до звуження функції відповідно на і . Нехай

,

.

Тоді є аналітичним продовженням вздовж ланцюга , , , .

3. Канонічний елемент. Продовження вздовж шляху. Канонічним елементом з центром в точці а називається упорядкована пара круга і голоморфної в ньому функції f. Функцію f голоморфну в крузі також називають канонічним елементом з центром в точці а . Канонічний елемент називається аналітичним продовженням елемента вздовж неперервного шляху , якщо існують точки , , і ланцюг канонічних елементів з центрами в точках , такі, що є аналітичним продовженням вздовж ланцюга . При цьому називають результатом аналітичного продовження вздовж , а , , – канонічними елементами, за допомогою яких здійснюється аналітичне продовження вздовж . Результатом аналітичного продовження називають також канонічний елемент . Якщо є результатом аналітичного продовження вздовж деякого неперервного шляху , то є результатом аналітичного продовження і вздовж деякої ламаної, яка з’єднує точки . Справді, досить з’єднати точки і ламаною, яка є об’єднанням відрізків таких, що , . З таких же міркувань випливає, що множина результатів аналітичного продовження вздовж гладких шляхів збігається з множиною результатів аналітичного продовження вздовж неперервних шляхів. Здійснення аналітичного продовження за допомогою канонічних елементів вздовж шляху є досить складною справою, оскільки воно пов’язане зі знаходженням сум степеневих рядів.

Приклад 1. Нехай

, ,

Канонічні елементи , є безпосереднім аналітичним продовженням один одного, бо і в D виконується , . Якщо взяти елемент , де , то він є безпосереднім аналітичним продовженням елемента , а також аналітичним продовженням елемента вздовж ланцюга , , , або вздовж ламаної, утвореної відрізками [0;i], [i;2].

Приклад 2. Нехай , і , де

, ,

.

Тоді , і відповідно в кругах , та . Кожний з канонічних елементів , і є безпосереднім аналітичним продовженням іншого. Можна також сказати, що є аналітичним продовженням вздовж ланцюга , а також вздовж ламаної, утвореної відрізками і .

Приклад 3. Нехай функція f є голоморфною в області і . Тоді канонічний елемент , де

допускає аналітичне продовження вздовж будь-якого спрямлюваного шляху такого, що а= і , причому результат аналітичного продовження в точку має вигляд

.

Справді, досить розглянути випадок, коли і , де – відстань від до . Тоді функція є голоморфною в і для . Звідси випливає потрібне.

4. Аналітичні функції. Канонічним елементом багатозначної функції , називається такий канонічний елемент , що і для всіх виконується . Повною аналітичною функцією називається така багатозначна функція , що: 1) має принаймні один канонічний елемент ; 2) кожний канонічний елемент , який є аналітичним продовженням вздовж деякого неперервного шляху, є канонічним елементом функції ; 3) для кожної точки функції знайдеться такий її канонічний елемент , що ; 4) кожні два її канонічні елементи є аналітичним продовженням один одного вздовж деякого неперервного шляху. Повну аналітичну функцію слід відрізняти від загальної аналітичної функції. Так називається така функція , яка володіє властивостями 1)-3).

Пагоном або відростком повної аналітичної функції в точці називається сукупність всіх елементів функції таких, що для всіх та виконується: і , коли .

Приклад 1. Функції

є загальними, але не є повними аналітичними функціями. Кожна ціла функція є повною аналітичною функцією. Функції також є, як буде показано далі, повними аналітичними функціями. Якщо – ціла функція, а – повна аналітична функція, то функція є повною аналітичною функцією. Сума і добуток двох повних аналітичних функцій є загальною аналітичною функцією, але не обов’язково є повною аналітичною функцією, оскільки і .

Теорема 1. Множина визначення повної аналітичної функції є областю.

Доведення. Справді, об’єднання кругів збіжності канонічних елементів розглядуваної функції є відкрита лінійно зв’язна множина. ►

Повною аналітичною функцією в області , називається така багатозначна функція , що: 1) має принаймні один канонічний елемент ; кожний канонічний елемент , який є аналітичним продовженням вздовж деякого неперервного шляху з , є канонічним елементом функції ; 3) для кожної її точки знайдеться такий її канонічний елемент , що ; кожні два її канонічні елементи є аналітичним продовженням один одного вздовж деякого неперервного шляху, який лежить в D. ►

Якщо дві повні аналітичні функції в області D мають спільний канонічний елемент з центром в точці a D, то вони є рівними, тобто рівними є їх множини точок.

Аналітичною функцією, називається така багатозначна функція , що: 1) має принаймні один канонічний елемент ; кожний її канонічний елемент є аналітичним продовженням вздовж деякого неперервного шляху; 3) для кожної її точки знайдеться такий її канонічний функції , що ; 4) кожні два її канонічні елементи є аналітичним продовженням один одного вздовж деякого неперервного шляху. Аналітична функція F однозначно визначається одним зі своїх канонічних елементів і множиною Г тих неперервних шляхів , аналітичним продовженням вздовж яких отримують всі інші канонічні елементи F . Тому аналітичну функцію F часто позначають так : . Наприклад, функція , , є аналітичною. Кожна голоморфна функція також є аналітичною.

Аналітичною гілкою функції F називається така аналітична функція f, яка має спільний з F канонічний елемент.

Функція називається аналітичною в області , якщо вона є аналітичною і .

Приклад 2. Функція , , є аналітичною.

Приклад 3. Функція , , є аналітичною в області .

Зауваження 1. Часто при розгляді аналітичного продовження розглядають канонічні елементи вигляду , де ,

,

, , ,

причому ці ряди збігаються для кожного і для кожного значення або , відповідно. Якщо , то таким f в точці а можна приписати значення

У випадках: ; узагальнений канонічний елемент називають відповідно: голоморфним (правильним); голоморфно-полярним (мероморфним); голоморфно-істотно особливим; голоморфно критичним; алгебраїчним (полярно-критичним, мероморфно-критичним); трансцендентним (критично істотно особливим). Відповідно називають повні аналітичні функції (з голоморфними елементами і т.д.). При цьому трансцендентний канонічний елемент називається безпосереднім аналітичним продовженням трансцендентного канонічного елемента , якщо і існують голоморфні гілки функцій , відповідно в деякій області , що .

5. Гармонійні функції і їх зв’язок із аналітичними. Функція називається гармонійною в області D, якщо вона має в D неперервні частинні похідні другого порядку і

(x; y)D. (1)

Оператор

називається оператором Лапласа.

Гармонійна в області D функції v називається спряженою до гармонійної в D функції u, якщо

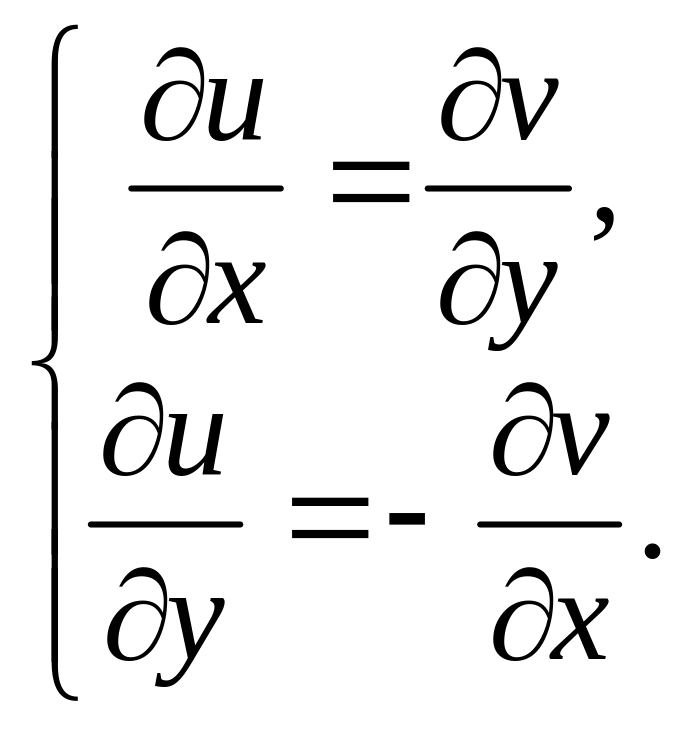(2)

Теорема 1. Для того, щоб функція була голоморфною в області D, необхідно і достатньо, щоб функції u та v були гармонійними функціями в області D і v була спряженою до u.

Доведення. Якщо функція є голоморфною, то вона має неперервні похідні всіх порядків. Тому функції u і v мають неперервні частинні похідні другого порядку і з умов Коші-Рімана маємо (2). З (2) випливає, що

,

Якщо функції u і v є гармонійними і виконуються умови (2), то функція має похідну в кожній точці , тобто є голоморфною. ►

Теорема 2. Нехай функція u є гармонійною в області D. Тоді в кожній однозв’язній області спряженою до u є гармонійна в G функція

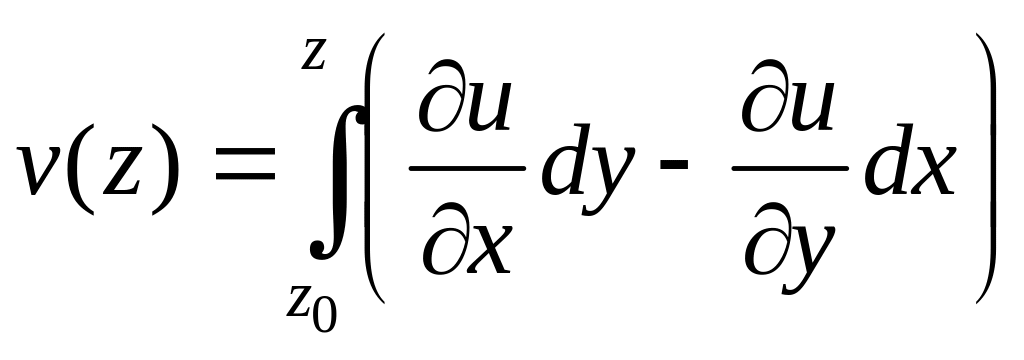, (3)

де – довільна точка області G. Якщо – інша спряжена до u функція, гармонійна в області G, то існує стала c₁ така, що .

Доведення. Нехай , . Тоді

, .

Тому криволінійний інтеграл (3) не залежить в G від шляху інтегрування. Крім цього, за властивостями криволінійних інтегралів

, .

Звідси випливає, що

, ,

тобто є спряженою гармонійною функцією. Якщо – інша спряжена гармонійна функція, то функції є голоморфною в D і , . Тому . Оскільки , то із умов Коші-Рімана, отримуємо, що

Тому не залежить від y і теорема 1 доведена. ►

Наслідок 1. Якщо функція u є гармонійною в однозв’язній області D, то існує функція v, гармонійна в D, яка є спряженою в D до .

Зауваження 1. Якщо область D не є однозв’язною, то в D однозначної спряженої гармонійної функції може не існувати. Наприклад, функція є гармонійною в області . Спряженою до неї в кожній однозв’язній області є однозначна і неперервна в цій області гілка функції . Функція є багатозначною спряженою гармонійною функцією. Багатозначна спряжена гармонійна функція також знаходиться за формулою (3). Але в багатозв’язній області інтеграл (3) може залежати від шляху інтегрування. Наприклад, так буде, якщо .

Приклад 1. Функція є гармонійною в , , . . 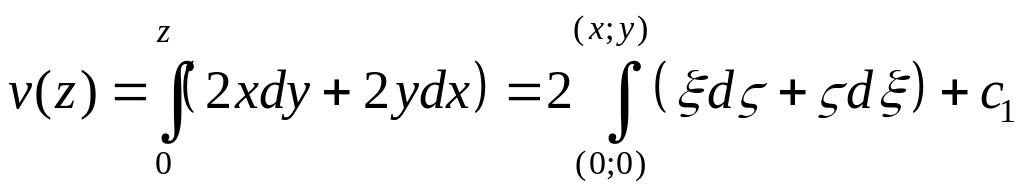Беручи інтеграл по відрізку , який з’єднує точки і , тобто по відрізку , , отримаємо .

Теорема 3 (єдиності). Якщо функція є гармонійною в області і дорівнює нулеві в деякому крузі , то для всіх .

Доведення. Нехай – довільна точка області і –гармонійна функція, яка є спряженою в до . Тоді функція є голоморфною в і з умов Коші-Рімана випливає, що є сталою. З’єднаємо точки і ламаною . Оскільки – компакт, то відстань між і є додатною і . Візьмемо на точки , , так, щоб , і довжина частини ламаної, яка лежить між точками була меншою за . Тоді , де . Нехай – гармонійна функція, яка є спряженою до в деякому крузі , . Тоді функція є голоморфною в і з умов Коші-Рімана випливає, що є сталою. Отже, є сталою в . Але круги і мають непорожній перетин. Тому для . Оскільки має скінчену довжину, то за скінчене число кроків ми прийдемо до круга і покажемо, що в цьому крузі. Тому і теорема доведена. ►

Зауваження 2. Теорему 3 можна розглядати як деякий аналог теореми єдиності для голоморфних функцій. Водночас, функція є гармонійною в і рівна нулеві на дійсній осі. Отже, аналогія з голоморфними функціями в цьому напрямку не йде дуже далеко.

Канонічним гармонійним елементом називається упорядкована пара круга і гармонійної в цьому крузі функції . За аналогією до означень безпосереднього аналітичного продовження та аналітичного продовження вздовж шляху можна сформулювати означення безпосереднього гармонійного продовження, гармонійного продовження вздовж шляху та означення повної гармонійної функції . При цьому виявляється, що кожна повна гармонійна функція є дійсною частиною деякої повної аналітичної функції.

6. Теорема про монодромію. Таку назву має наступне твердження.

Теорема 1. Якщо багатозначна функція є аналітичною в однозв’язній області D і деякий, а, отже, і кожний, її канонічний елемент можна продовжити вздовж будь-якого неперервного шляху із , то є голоморфною в D.

Доведення. Оскільки , то досить показати, що F є однозначною функцією. Припустимо протилежне. Тоді існують канонічний елемент функції F з центром в точці а і замкнена ламана q із D з початком в точці а такі, що результат аналітичного продовження вздовж q не збігається з . Звідси випливає, що існує трикутник , , і канонічний елемент з центром в одній із його вершин такі, що результат аналітичного продовження f₁ вздовж є відмінним від . Розбиваючи трикутник середніми лініями на чотири рівних прийдемо до трикутника і канонічного елемента з центром в одній із вершин таких, що результат аналітичного продовження вздовж є відмінним від і площа дорівнює четвертині площі . Продовжуючи цей процес одержимо послідовність ( ) трикутників з властивостями: а) б) послідовність площ цих трикутників є збіжною до 0; в) трикутники мають єдину спільну точку , в будь-якому околі U якої знайдуться такі трикутник і канонічний елемент функції F з центром в точці , аналітичне продовження вздовж не збігається з . Отже, мусить існувати неперервний шлях в з кінцем в точці , вздовж якого деякий канонічний елемент функції F не продовжується. Cуперечність. ►

Теорема 2. Якщо канонічний елемент з центром в точці допускає аналітичне продовження вздовж будь-якого неперервного шляху , який лежить в області D, а шляхи і є гомотопними в області D і мають спільний початок у точці а, то результати аналітичного продовження вздовж і співпадають.

Доведення. Справді, оскільки шляхи і є гомотопними і мають спільний початок, то вони мають і спільний кінець. Тому існує однозв’язна область така, що ₁ і функція , де Г – множина всіх неперервних шляхів, які мають спільний початок в точці і лежать в G, є аналітичною в G і не має в G особливих точок. Тому твердження теореми 2 випливає з теореми про монодромію.►

Теорема 3 (Пуанкаре). Якщо F – повна аналітична функція, то для кожного множина є зліченною або скінченою.

Доведення. Справді, нехай – деякий канонічний елемент такий, що і . Кожне число є значенням деякого канонічного елемента з центром в точці b, який є аналітичним продовженням вздовж ламаної, яка з’єднує точки а і b. Можна вважати, що всі відмінні від а та b вершини цієї ламаної є такими, що числа та є раціональними, оскільки різних таких ламаних є зліченна кількість, то звідси випливає твердження теореми. ►

Приклад 1. Для кожного множина = є зліченною.

Аналітичним продовженням функції з множини в область називається така аналітична в функція , що . Якщо множина є областю або неперервною кривою і функція є неперервною на , то аналітичне продовження, якщо воно існує, єдине, що випливає з теореми єдиності для голоморфних функцій та теореми Пуанкаре.