
- •Министерство образования и науки рф ни Иркутский государственный технический университет математичесКая логиКа
- •Иркутск 2010
- •I.Ответьте на следующие вопросы:
- •II.Выполните следующие упражнения:
- •I.Ответьте на следующие вопросы:
- •II.Выполните следующие упражнения:
- •I.Ответьте на следующие вопросы.
- •II.Выполните следующие упражнения:
- •I.Ответьте на следующие вопросы:
- •I.Ответьте на следующие вопросы:
- •II.Выполните следующие упражнения:
- •(Силлогизма);
- •(Контропозиции).
- •I.Ответьте на следующие вопросы:
- •II.Выполните следующие упражнения:
- •I.Ответьте на следующие вопросы:
- •II.Выполните следующие упражнения:
I.Ответьте на следующие вопросы:
Дайте определение исчисления предикатов.
Какое исчисление предикатов называется чистым (прикладным)?
Какое исчисление предикатов называется исчислением первого порядка (высших порядков)?
Что понимают под интерпретацией исчисления предикатов?
Какие формулы исчисления предикатов называются общезначимыми?
Как определяется полнота исчисления предикатов?
Дайте определения логического следствия и логической эквивалентности.
Сформулируйте задачу автоматического доказательства теорем.
Сформулируйте принцип «доказательства от противного»
Приведите алгоритм сведения формул к предложениям.
Запишите правило резолюций для исчисления предикатов.
Приведите алгоритм опровержения методом резолюций.
Рассмотрим один из возможных вариантов построения исчисления
предикатов
Алфавит:
 -
предметные переменные;
-
предметные переменные; -
предметные константы;
-
предметные константы; -
символы (буквы) n-местных
предикатов;
-
символы (буквы) n-местных
предикатов; -
символы (буквы) n-местных
функция;
-
символы (буквы) n-местных
функция; -
логические символы;
-
логические символы;- технические символы.
Слово – конечная последовательность букв алфавита.
Терм:
всякая предметная переменная и константа есть терм;
если
 - n-местный
функциональный символ и
- n-местный
функциональный символ и
 - термы, то слово
- термы, то слово
 - терм;
- терм;никаких термов, кроме построенных по пп. а) и б), нет.
Атомарная
формула –
это слово
 ,
где
,
где
 - n-местный
предикатный символ, а
- термы.
- n-местный
предикатный символ, а
- термы.
Формула:
атомарная формула есть формула;
если А и В – формулы, то слова
 - формулы;
- формулы;никаких формул, кроме построенных по пп. a) и б) нет.
Понятия вывода и выводимой формулы определяются аналогично соответствующим понятиям для исчисления высказываний.
Аксиомы:
;
;
;
;
;
;
;
;
;
;
;
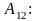
 ;
;

 .
.
В схемах аксиом 1-11 A, B, C – любые формулы; В схемах аксиом 12-13 A(x) – формула, t – терм, свободный для x в A(x), A(t) – формула, полученная из A(x) заменой всех свободных вхождений x на t.
Правила вывода:
 (modus
ponens);
(modus
ponens); (
-
введения);
(
-
введения); (
-
удаления);
(
-
удаления);
причем, в правилах (2) и (3) x не входит свободно в A, a y не входит свободно в B(x).
II.Выполните следующие упражнения:
Доказать следующие правила:
 (переименование
свободных переменных), где все свободные
вхождения x
в A(x)
не содержатся
в области действия квантора по y;
(переименование
свободных переменных), где все свободные
вхождения x
в A(x)
не содержатся
в области действия квантора по y; (переименование
связных переменных);
(переименование
связных переменных);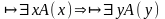 (переименование
связных переменных);
(переименование
связных переменных);
В правилах б) и в) A(x) не содержит свободного вхождения y и свободные вхождения x не входят в область действия квантора по у.
 (
- удаление);
(
- удаление); (
- введение);
(
- введение);
В правилах г) и д) t – терм свободных для x в A(x), A(t) – формула, полученная из A(x) заменой всех свободных вхождений x на t.
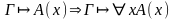 (
- введение), где x
не входит свободно в формулы из Г;
(
- введение), где x
не входит свободно в формулы из Г;
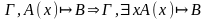 (
- удаление), где x
не входит свободно ни в формулу из Г,
ни в формулу и B;
(
- удаление), где x
не входит свободно ни в формулу из Г,
ни в формулу и B;(Силлогизма);
(Контропозиции).
Построить вывод следующих формул:
 ;
;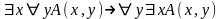 ;
;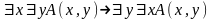 ;
; ;
;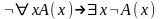 ;
; ;
; ;
; ;
; ;
; .
.
Доказать, что:
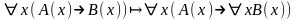 ;
; ;
;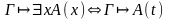 ,
для некоторого терма t
свободного для x
в A(x);
,
для некоторого терма t
свободного для x
в A(x); ,
для любого терма t
свободного для x
в A(x).
,
для любого терма t
свободного для x
в A(x).
Пусть A не содержит x свободно. Доказать, что:
 ;
; ;
; ;
;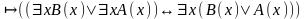 ;
; ;
; ;
;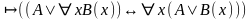 ;
;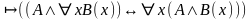 ;
; ;
; ;
;
Выводимы ли в исчислении предикатов следующие формулы:
 ;
; ;
;;
 ;
; ;
; ;
; ;
; ;
; ;
; .
.
Свести к предложениям следующие формулы:
;
;
;
;
;
Индивидуальные задания
1) Свести к предложениям следующие формулы:
2) выполнить унификацию дизъюнктов.
№варианта |
Формула
|
|
|
∀x(A(x)→B(y))&∀y(A(x)→(B(y)→C(z)))→ A(x) |
|
|
∀x(B(x)→∃z(A(z)))&∃y(A(z)→C(y))→ ¬C(y) |
|
|
∀x(A(x)→∃y(B(y)))→∃y(¬A(x)∨¬C(z)∨B(y)) |
|
|
∀x(A(x)→∃z(C(z)))&∀y(C(z)→B(y))→(A(x)→B |
|
|
∀x(A(x)→B(y))&∀y(A(x)→(B(y)→C(z) |
|
|
∀x(A(x)→∃y(B(y)→C(z)))→∀z(A(x)&B(y)→C(z) |
|
|
∀x(A(x)→B(z))&∀y(C(y)→A(x))→∃z(C(y)→B(z) |
|
|
∀x((A(x)→B(y))→∀y((C(y)∨A(x)))→C(y) |
|
|
∀x(A(x)→B(y))&∀y(A(x)→(B(y)→C(z)))→(A(x) |
|
|
∀x(A(x)→B(y)&A(x)→∀y(B(y)→C(z)))→(A(x) |
|
|
∀x(A(x)→∃z(B(y)→C(z)))→∀y(B(y)→(A(x)→C(x)) |
|
|
(∀x(A(x))→∃z(B(z)))→∀z((B(x)→C(z))→(A(x) |
|
|
(∃x(¬A(x))→∀z(¬B(z)))→(¬B(x)∨A(x)) |
|
|
(∀x(A(x))→∀y(B(y)))→∃y(C(y)&A(x)→C(y)&B |
|
|
∀x(¬A(x)→∃y(B(y)))→(¬B(y)→A(x)) |
|
|
∀x(B(x)→∃z(A(z)))&∃y(A(z)→C(y))→(¬C(y) |
|
|
∀x(A(x)→∃z(C(z)))&∀y(C(z)→B(y))→(A(x)→B |
|
|
∀x(¬A(x)→∃y(¬B(y)))→(B(y)→A(x)) |
|
|
∀x(A(x)→B(x))&∃y(B(x)→C(y))→∃z(C(y)→D(z |
|
|
∀x(A(x)→B(x))&∀z(C(z)→A(x))→∃y(C(z)→B(y |
|
|
∀x(B(x)→∀y(A(y)))&∀y(B(y)→(A(x)→C(z)))→ |
|
|
∀x(A(x)→B(y)&A(x)→∀y(B(y)→C(z)))→(A(x) |
|
|
∀x(A(x)→B(x))→(∀y(C(y)→A(x))→∃z(C(z)→B |
|
|
1 |
|
|
∀x(B(x)→A(y))&(B(x)→∀y(A(y)→C(z)))→∃z(C |
|
|
(∃x(A(x)→B(z))→∃y(C(y)∨A(x)))→∀z(C(y)∨B(z |
|
|
(∀x(B(x))→∃y(A(y)))&(A(y)→∃yC(y))→(¬A(x) |
|
|
((∀x(A(x))→∃x(B(x)))→∃y(A(x)∨C(y)))→(B(x) |
|
|
∃x(A(x)→∀y(B(y)))&(¬A(x)→∀y(B(y)))→B(y) |
|
|
∀x(A(x)→∃y(B(y)))&(¬A(x)→B(x))→B(x) |
|
|
∀x(A(x)→B(x))&∀z(C(z)→A(x))→∃y(C(z)→B( |
|
|
(∃x(B(x))→∀y(A(y)))&(¬B(x)→A(y))→A(z) |
|
|
(∀x(B(x))→∃z(C(z)))→(A(y)&B(x)→A(y)&C(z) |
|
|
∃x(A(x)→B(y))→∀y∀z((C(z)→A(x))→(C(z)→B |
|
|
(∀x(A(x))→∃z(C(z)))&∀y(C(z)→B(y))→A(x) |
|
|
∀x(A(x))→∃y(B(y))&∀y(C(y)→∃xD(x))→(A(x) |
|
|
∀x(A(x)→B(y))&∀z(C(z)→A(x))→∃y(C(z)→B(z) |
|
|
(∀x(A(x)→∃z(B(z)))→∃y(A(x)∨C(y)))→(B(z)∨C |
|
|
∀x(B(x)→∀y(A(y)))&∀y(B(x)→(A(y)→C(z)))→ |
|
|
∀x(B(x)→A(y))&(B(x)→∀y(A(y)→C(z)))→∃z(B |
|
|
∀x(A(x)→B(x))→∀y((C(y)→A(x))→(C(y)→B(x |
|
|
∀x(A(x)→B(y))&(A(x)→∀y(B(y)→C(z)))→(A(x |
|
|
(∀x(B(x))→∃z(C(z)))→(A(y)&B(x)→A(y)&C(z) |
|
|
∃x(A(x)→B(z))→∃y((C(y)∨A(x))→∀z(C(y)∨B(z) |
|
|
∀x(A(x)→B(y))&∀z(C(z)→A(x))→∃y(C(z)→B(y) |
|
|
∀x(A(x)→B(x))&∃y(B(x)→C(y))&∃z(C(y)→D(z) |
|
|
(∀x(B(x)→∃y(A(y))))&∃y(A(x)→C(y))→¬C(y) |
|
|
(∀x(A(x))→∃z(C(z)))&∀y(C(z)→B(y))→(A(x) |
|
|
∀x(A(x)→B(y))&∀y(A(x)→(B(y)→C(z))) |
Занятие №6
Тема: Теория алгоритмов. Машины Тьюринга.
