I.Ответьте на следующие вопросы:

1. К какому типу математических теорий относятся исчисления высказываний?

2. Каким образом определяется формальная аксиоматическая теория?

3. Какие аксиоматизации исчисления высказываний вам известны?

4. Дайте определение непосредственной выводимости формулы по правилу вывода.

5. Что называется выводом формулы в формальной теории? Что называется теоремой

6. Какова связь между формулами алгебры высказываний и исчисления высказываний?

7. Дайте определение полноты исчисления высказываний.

8. Какая система аксиом исчисления высказываний называется независимой?

9. Дайте определение непротиворечивости исчисления высказываний.

10. Сформулируйте теорему дедукции.

11. Запишите правило резолюций для исчисления высказываний

12. Приведите алгоритм опровержения методом резолюций.

II. Выполнить упражнения.

Рассмотрим один из возможных вариантов построения исчисления высказываний (обозначим его L₁ ).

Алфавит:

1. - пропозициональные переменные;

2. - логические символы;

3. - технические символы.

Правило построение формул:

1. всякая пропозициональная переменная – формула;

2. если А и В – формулы, то - формулы;

3. других формул нет.

Аксиомы. Пусть А, В, С – произвольные формулы, тогда следующие формулы являются аксиомами:

;

;

;

;

;

;

;

;

;

;

.

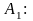
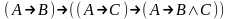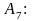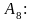
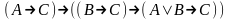Правило вывода - Modus Ponens

M.P.

1. В данном исчислении построить вывод следующих формул:

1. ;

2. ;

3. ;

2. Пользуясь теоремой дедукции построить вывод следующих формул:

1. ;

2. ;

3. ;

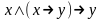3. Доказать, что:

1. А ,В |— А В;

2. А |—( В→А);

3. А |—( В А);

4. ¬А ¬В |— ¬(А В) ;

5. В |—( А В);

6. А→(В→С) |— (А В) →С (правило соединения посылок);

7. А→В, В→С |— А→С (правило разъединения посылок);

8. А (В→С) |— А→(В→С) (правило силлогизма) ;

9. А→ (В→С) |—( В →(А →С)) (правило перестановки посылок);

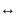10. А, В |— А В;

4. Доказать методом резолюций:

1. (A&B →C), (C&D →¬ M), ( ¬N →D&M) |— (A&B →N) ;

2. (A →B)&(C →D), (D&B→ M), ¬M|—(¬A ∨¬C) ;

3. ((¬ A ∨¬ B∨ ¬ A& ¬ B) → C), ((A ∨B ∨A&B) →¬C)|—(C →¬A).

Индивидуальные задания

Задание 1

В исчислении L₁ п. II построить вывод следующих формул:

№ варианта
	;
	;
	;
	;
	;
	;

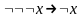Пользуясь теоремой дедукции построить вывод следующих формул:

№ варианта

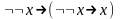
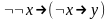
Доказать, что в исчислении высказываний L₂.

.

№ варианта
	формула II + III = IIIII выводима
	формула I + I = I не выводима

Доказать, что в исчислении L₄ имеют место следующие утверждения:

№ варианта
	А → (B → C) | — B → (A → C)
	А→ (B → C) ,А ,В| — C
	А→В| — С∨А→С∨В
	| — (А→В) →((С→А)→(С→В))
	С→А, А→В| — С→В
	| — ¬В→(В→С)
	| — ¬В→¬¬В→С

Доказать, что в исчислении L₅ справедливы утверждения.

№ варианта
	А→В,В→С| — ¬ (¬С&А)
	| — ¬ (¬А&А)
	| — ¬ ¬А→А
	| — ¬ (А&В)→(В→¬ А)

Доказать, что в исчислении L₆ справедливы утверждения.

№ варианта
	| — (А→В) →((С→А)→(С→В))
	С→А, А→В| — С→В
	| — ¬В→(В→С)
	| — ¬В→¬¬В→С

Задание 2

Проверить, используя правило резолюций

1. (A→B), (C→D), (B→¬D) ,C |⎯ (¬A∨¬D)

2. (A→B), (C→B) ,(B→D), ¬D |⎯ (¬A&¬C)

3. (A→B), (C→¬B), (¬C&D) |⎯ A

4. (A→B), (D→C), ¬B ,¬C |⎯ ¬( A∨D)

5. (A→B), (C→¬B), (C&¬D) |⎯ ¬ (¬A→D)

6. (A→B) ,(B→C) ,(C→D) ,A&B |⎯ B&D

7. (A→B), (D→C), ¬(B∨C) |⎯ (¬A&¬D)

8. (A→B), (B→C) ,(D→C) ,(A∨D) |⎯ (C∨D)

9. 4 (A→B), (B&D →C) ,(A&D) |⎯ C

10. (A→B), (A→(B→C)), (A&D) |⎯ C

11. (A→B), (C→B) ,(D→(A∨C)) ,D |⎯ B

12. (A→B), (B→C), (C→D), A&B |⎯ B&D

13. (A→(B→C)), (¬D∨A), B |⎯ (¬D∨C)

14. (A→(B→C)) ,(D∨A) ,B, D |⎯ C

15. (A→(B→C)), (A→B) ,A&D |⎯ C&D

16. (A→(B→C)), (¬ D∨A) ,B |⎯ (D∨C)

17. (A→(B→C)), (⎤ D∨A), B |⎯ (D→C)

18. (A→(B→C)) ,((A→C)→D), ¬D |⎯ ¬B

19. (B→A), (B→(A→C)), B&D |⎯ C

20. (B→A), (B→(¬A∨C)), (B&D) |⎯ C&D

21. (B→A), (A→C), (D→C) ,(B∨D) |⎯ (C∨D)

22. (B→(A→C)), (B→A), (C→D), ¬D |⎯ ¬B

23. (¬A∨B), (C∨¬B) ,(¬С&¬D) |⎯ ¬(A∨D)

24. (¬A∨¬B) ,(C→A), (B∨¬D) |⎯ (¬C∨¬D)

25. (¬A∨B) ,(C∨¬B), (A∨D) ,¬D |⎯ C

26. (¬A∨¬B), (C→A), B&D|⎯D→C

27. (A∨B) ,(A→C), (B→D) ,¬C |⎯ D

28. (A∨B), (C→ B), ¬(C→B) |⎯ ¬(¬A→B)

29. (A↔B), (A→(B∨C)), (D∨B) |⎯ (¬C→D)

30. (A&B→C) ,(¬D∨¬C), D |⎯ ¬A∨¬B)

Приложение

1. Исчисление высказываний L₂.

Список термов исчисления: {I, +, =}

Правила образования формул:

а) I - формула;

б) если  - формула, то I - также формула;

в) если  и  - формулы, то  +  и  =  также формула.

Задана единственная аксиома I+I = II и

два правила вывода: а) если ₁+I = ₂ – выводимая формула, то ₁I+I = ₂I также выводимая формула; б) ₁+₂ = ₃ – выводимая формула, то ₁+₂I = ₃I – также выводимая формула.

2. Исчисление высказываний L₃ (исчисление Лукасевича).

Множество термов состоит из бесконечного числа букв и знаков  , .

Правила образования формул:

а) все буквы есть суть формулы;

б) если  - формула, то  - также формула;

в) если  и  - формулы, то    также формула.

Система аксиом следующая:

1. (A  B)  ((B  C)  (A  C));

2. (A A) A;

3. A  (A  B).

Справедливы правило подстановки и правило заключения.

3. Исчисление высказываний L₄ (Гильберт и Аккерман, 1938).

• Связки: , (А  В :=  А В).

• Аксиомы:

1. А A  А,

2. А  А В,

3. А В  В А,

4. (В  С)  (А В  А С).

• Правило: Modus ponens.

4. Исчисление высказываний L₅ (Россер, 1953).

.

Связки: &, , (А  В :=  (А&  В)).

Аксиомы:

1. А  А & А,

2. А & В  А,

3. (А  В)  ( (В & С)   (С & А)).

Правило: Modus ponens.

5. Исчисление высказываний L₆ (Клини, 1952).

• Связки: , &, , .

• Аксиомы:

1. А  (В  А),

2. (А  (В  С))  ((А  В)  (А  С)),

3. А & В  А,

4. А & В  В,

5. А  (В  (А & В)),

6. А  (А В),

7. В  (А В),

8. (А  С)  ((В  С)  ((А В)  С)),

9. (А  В)  ((А   В)   А,

10. А  А.

• Правило: Modus Ponens.

Занятие №5

Тема: Исчисление предикатов.