
- •Міністерство освіти і науки України
- •Правила оформлення контрольної роботи:
- •Основні питання програми
- •Модуль 1 Системи рівнянь, вектори та аналітична геометрія
- •1.1. Визначники, матриці, розв’язання систем лінійних рівнянь
- •1.2. Елементи векторної алгебри
- •1.3. Пряма на площині
- •1.4. Криві другого порядку
- •1.5. Площина та пряма в просторі
- •Модуль 2 вступ в математичний аналіз
- •2.1. Розкриття невизначеностей, і і іі визначні границі
- •2.2. Диференціальне числення функцій однієї змінної
- •Основні правила диференціювання:
- •2.3. Застосування похідних для дослідження функцій
- •2.4. Похідні в механіці
- •2.5. Диференціальне числення функцій декількох змінних
- •Модуль 3 нЕвизначений і визначений інтеграли
- •3.1. Основні методи інтегрування
- •Основні властивості невизначеного та визначеного інтегралів:
- •3.2. Невласні інтеграли
- •3.3. Застосування визначених інтегралів
- •Модуль 4 диференціальні рівняння
- •4.1. Розв’язання диференціальних рівнянь деяких типів
- •Модуль 5 кратні, криволінійні та поверхневі інтеграли
- •5.1. Подвійні, потрійні інтеграли та їх застосування
- •5.2. Криволінійні інтеграли
- •Модуль 6 числові і степеневі ряди
- •6.1. Числові ряди
- •Ознака Даламбера. Якщо для знакододатного ряду існує
- •(Границя відношення наступного члена до попереднього), то
- •Радикальна ознака Коші. Якщо для ряду, загальний член якого , існує
- •6.2. Степеневі ряди
- •Модуль 7 комплексні числа. Елементи теорії функцій комплексної змінної
- •7.1. Комплексні числа
- •7.2. Обчислення значень елементарних функцій
- •Модуль 8. Теорія ймовірностей і елементи математичної статистики
- •8.1. Основні поняття і теореми теорії ймовірностей
- •8.2. Дискретні випадкові величини
- •8.3. Неперервні випадкові величини
- •8.4. Біноміальний та пуассонів закони розподілу
- •8.5. Нормальний, рівномірний та показниковий закони
- •Числові характеристики:
- •8.6. Елементи математичної статистики
- •Контрольна робота № 1 Модуль 1. Системи рівнянь, вектори та аналітична геометрія
- •Модуль 2. Вступ в математичний аналіз
- •Модуль 3. Невизначений і визначений інтеграли
- •Модуль 4. Диференціальні рівняння
- •Контрольна робота № 2 Модуль 5. Кратні, криволінійні та поверхневі інтеграли
- •Модуль 6. Числові і степеневі ряди
- •Література
- •Продовження додатка а
- •Додаток б
- •Продовження додатка б
- •Додаток в Значення (розподіл Пуассона)
- •Продовження додатка в Значення (розподіл Пуассона)
Модуль 2 вступ в математичний аналіз
2.1. Розкриття невизначеностей, і і іі визначні границі
Обчислення границь базується на таких основних теоремах:
Якщо існують
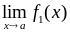 і
і
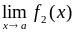 ,
то:
,
то:

![]() ,
(2.1.1)
,
(2.1.1)
![]() ,
(2.1.2)
,
(2.1.2)
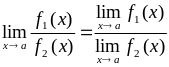
![]() ,
(2.1.3)
,
(2.1.3)
![]() .
(2.1.4)
.
(2.1.4)
Перша визначна границя:
![]() .
(2.1.5)
.
(2.1.5)
Друга визначна границя:
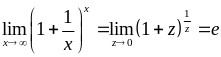 .
(2.1.6)
.
(2.1.6)
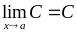 ;
;
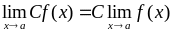 ,
(
‑ стала
величина). (2.1.7)
,
(
‑ стала
величина). (2.1.7)Для всіх неперервних функцій
![]() .
(2.1.8)
.
(2.1.8)
Слід пам'ятати, що (для
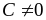 ):
):


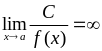 ,
якщо
,
якщо
![]() ;
;
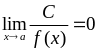 ,
якщо
,
якщо
![]() .
.
Щодо
техніки обчислення границь, слід
відзначити, що в найпростіших випадках
знаходження границі зводиться до
підстановки у вираз під знаком границі
граничного значення аргументу. Але
часто така підстановка призводить до
невизначених виразів виду
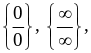
![]() Знаходження границь у цих випадках
називається розкриттям невизначеності.
Знаходження границь у цих випадках
називається розкриттям невизначеності.
Наприлад,
якщо невизначеність
![]() з’явиться,
коли в чисельнику (знаменнику) є
ірраціональний вираз, тоді треба
позбутися ірраціональність у чисельнику
(знаменнику) шляхом помноження на
"спряжений" вираз.
з’явиться,
коли в чисельнику (знаменнику) є
ірраціональний вираз, тоді треба
позбутися ірраціональність у чисельнику
(знаменнику) шляхом помноження на
"спряжений" вираз.
Невизначеність
виду
при наявності тригонометричних функцій
розкривається за допомогою першої
визначної границі та часто вимагає
попередніх тотожних перетворень
(наприклад, за допомогою формул:
![]() ,
,
![]() ,
,
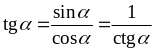 ,
,
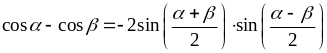 ).
).
Друга
визначна границя розкриває невизначеність
![]() .
Наслідками (2.1.6) є вирази:
.
Наслідками (2.1.6) є вирази:
![]() ,
,
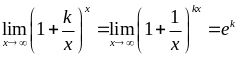 .
(2.1.9)
.
(2.1.9)
Приклад 2.1.1.
Знайти
границі:
1) 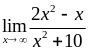 ,
2)
,
2) ![]() ,
3)
,
3) ![]() .
.
Розв’язання.
1) Маємо
невизначеність
![]() .
Винесемо в чисельнику і знаменнику
старший ступінь змінної і скоротимо:
.
Винесемо в чисельнику і знаменнику
старший ступінь змінної і скоротимо:
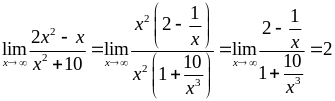 (тому,
що
(тому,
що
![]() ,
,
![]() ).
).
Аналогічно,
2) 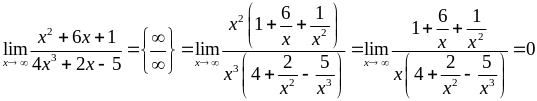 ;
;
3) 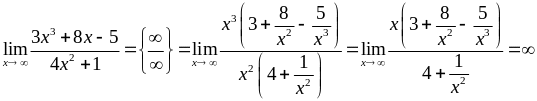 .
.
Приклад 2.1.2.
Обчислити
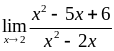 .
.
Розв’язання.
В даному випадку користуватися формулою
(2.1.3) не можна, тому що границя знаменника
дорівнює нулеві. Безпосередня же
підстановка у вираз під знаком границі
граничного значення аргументу
![]() приводить
до невизначеності
.
приводить
до невизначеності
.
Розкладемо
на множники чисельник і знаменник.
(Зауважимо, що
![]() ,
якщо
,
якщо
![]() ‑ корені). Коренями квадратного
рівняння
‑ корені). Коренями квадратного
рівняння
![]() є
є
![]() ,
,
![]() ,
значить
,
значить
![]() .
.
Отже, за рахунок розкладання на множники і скорочення, позбавляємось невизначеності, після чого в результаті підстановки в отриманий вираз маємо
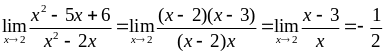 .
.
Приклад 2.1.3.
Обчислити
1) 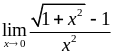 ,
2)
,
2) ![]() .
.
Розв’язання.
1) Підстановка
у вираз (під знаком границі)
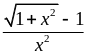 значення
значення
![]() приводить до невизначеності
.
Для її розкриття помножимо чисельник
і знаменник на вираз, що "спряжений"
з чисельником (користуючись формулою
скороченного множення
приводить до невизначеності
.
Для її розкриття помножимо чисельник
і знаменник на вираз, що "спряжений"
з чисельником (користуючись формулою
скороченного множення
![]() ).
Після цього скоротимо на
).
Після цього скоротимо на
![]() і одержимо:
і одержимо:
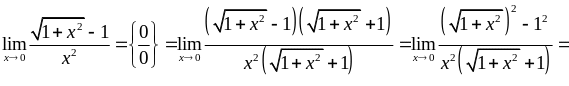
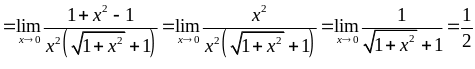 .
.
2) У
випадку
маємо невизначеність
![]() .
Помноження і ділення виразу під знаком
границі на "спряжений" з ним вираз
.
Помноження і ділення виразу під знаком
границі на "спряжений" з ним вираз
![]() з урахуванням (2.1.7)) дає:
з урахуванням (2.1.7)) дає:
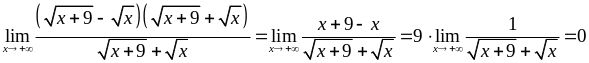 .
.
Приклад 2.1.4.
Знайти
границі: 1) 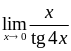 ,
2)
,
2) 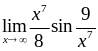 ,
3)
,
3) ![]() .
.
Розв’язання.
Враховуючи, що
![]() ,
,
![]() ,
за допомогою формул тригонометрії,
властивості (2.1.2) та першої визначної
(2.1.5) маємо:
,
за допомогою формул тригонометрії,
властивості (2.1.2) та першої визначної
(2.1.5) маємо:
1) 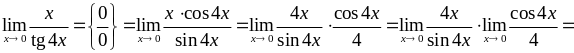
![]() ,
,
2) 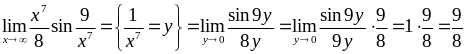 ,
,
3) 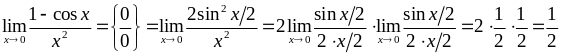 .
.
Приклад 2.1.5.
Знайти
границі: 1) 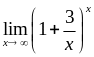 ,
2)
,
2) 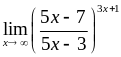 .
.
Розв’язання. Маємо невизначеність , яка розкривається за допомогою другої визначної границі (2.1.6).
1) 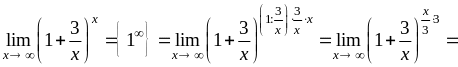
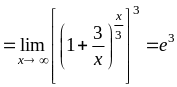 (відповідь
у данному випадку можна було отримати
безпосередньо за (2.1.9)).
(відповідь
у данному випадку можна було отримати
безпосередньо за (2.1.9)).
2) 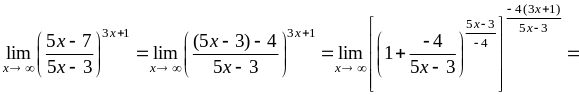
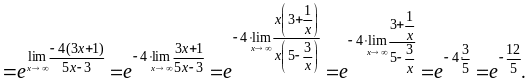
Зауважимо, що приклади 2.1.1 – 2.1.5 відповідають завданню 2.1 контрольної роботи.
Література: [1, с. 93 ‑ 125], [2, с. 101 ‑ 134], [3, с. 172 – 208, 247 ‑ 264], [7].
