
- •Міністерство освіти і науки України
- •Правила оформлення контрольної роботи:
- •Основні питання програми
- •Модуль 1 Системи рівнянь, вектори та аналітична геометрія
- •1.1. Визначники, матриці, розв’язання систем лінійних рівнянь
- •1.2. Елементи векторної алгебри
- •1.3. Пряма на площині
- •1.4. Криві другого порядку
- •1.5. Площина та пряма в просторі
- •Модуль 2 вступ в математичний аналіз
- •2.1. Розкриття невизначеностей, і і іі визначні границі
- •2.2. Диференціальне числення функцій однієї змінної
- •Основні правила диференціювання:
- •2.3. Застосування похідних для дослідження функцій
- •2.4. Похідні в механіці
- •2.5. Диференціальне числення функцій декількох змінних
- •Модуль 3 нЕвизначений і визначений інтеграли
- •3.1. Основні методи інтегрування
- •Основні властивості невизначеного та визначеного інтегралів:
- •3.2. Невласні інтеграли
- •3.3. Застосування визначених інтегралів
- •Модуль 4 диференціальні рівняння
- •4.1. Розв’язання диференціальних рівнянь деяких типів
- •Модуль 5 кратні, криволінійні та поверхневі інтеграли
- •5.1. Подвійні, потрійні інтеграли та їх застосування
- •5.2. Криволінійні інтеграли
- •Модуль 6 числові і степеневі ряди
- •6.1. Числові ряди
- •Ознака Даламбера. Якщо для знакододатного ряду існує
- •(Границя відношення наступного члена до попереднього), то
- •Радикальна ознака Коші. Якщо для ряду, загальний член якого , існує
- •6.2. Степеневі ряди
- •Модуль 7 комплексні числа. Елементи теорії функцій комплексної змінної
- •7.1. Комплексні числа
- •7.2. Обчислення значень елементарних функцій
- •Модуль 8. Теорія ймовірностей і елементи математичної статистики
- •8.1. Основні поняття і теореми теорії ймовірностей
- •8.2. Дискретні випадкові величини
- •8.3. Неперервні випадкові величини
- •8.4. Біноміальний та пуассонів закони розподілу
- •8.5. Нормальний, рівномірний та показниковий закони
- •Числові характеристики:
- •8.6. Елементи математичної статистики
- •Контрольна робота № 1 Модуль 1. Системи рівнянь, вектори та аналітична геометрія
- •Модуль 2. Вступ в математичний аналіз
- •Модуль 3. Невизначений і визначений інтеграли
- •Модуль 4. Диференціальні рівняння
- •Контрольна робота № 2 Модуль 5. Кратні, криволінійні та поверхневі інтеграли
- •Модуль 6. Числові і степеневі ряди
- •Література
- •Продовження додатка а
- •Додаток б
- •Продовження додатка б
- •Додаток в Значення (розподіл Пуассона)
- •Продовження додатка в Значення (розподіл Пуассона)
Модуль 5 кратні, криволінійні та поверхневі інтеграли
5.1. Подвійні, потрійні інтеграли та їх застосування
Основні види простих областей інтегрування на площині:
Область інтегрування
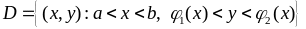 є стандартною
відносно вісі
.
Вона обмежена зліва і справа прямими
і
є стандартною
відносно вісі
.
Вона обмежена зліва і справа прямими
і

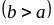 ,
а знизу і зверху – неперервними кривими
,
а знизу і зверху – неперервними кривими
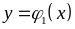 і
і

 ,
кожна з яких перетинається вертикальною
прямою
,
кожна з яких перетинається вертикальною
прямою
 (для будь-якого
(для будь-якого
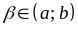 ),
лише в одній точці.
),
лише в одній точці.
Для такої області подвійний інтеграл обчислюється за формулою:
 ,
(5.1.1)
,
(5.1.1)
причому
спочатку обчислюється за змінною
“внутрішній” інтеграл
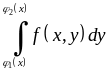 ,
в якому
вважається сталим.
,
в якому
вважається сталим.
Область інтегрування
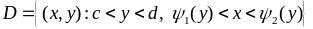 є стандартною
відносно вісі
є стандартною
відносно вісі
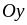 .
Вона обмежена знизу і зверху прямими
.
Вона обмежена знизу і зверху прямими
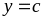 і
і

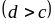 ,
а справа а зліва – відповідно неперервними
кривими
,
а справа а зліва – відповідно неперервними
кривими
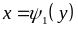 і
і
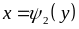
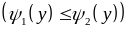 ,
кожна із яких перетинається довільною
горизонтальною прямою
,
кожна із яких перетинається довільною
горизонтальною прямою
 (для будь-якого
(для будь-якого
 )
лише в одній точці.
)
лише в одній точці.
Для такої області подвійний інтеграл обчислюється за формулою:
 ,
(5.1.2)
,
(5.1.2)
причому
спочатку обчислюється за змінною
“внутрішній” інтеграл
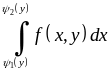 ,
в якому
вважається сталим.
,
в якому
вважається сталим.
Праві частини формул (5.1.1), (5.1.2) називаються двократними, або повторними інтегралами. Таким чином, подвійний інтеграл обчислюється за допомогою зведення його до повторного інтеграла. Якщо область не є стандартною, то як часто трапляється, її можна представити у вигляді об’єднання стандартних множин.
Перетворення
подвійного інтеграла в прямокутних
декартових координатах
![]() до інтеграла в полярних
координатах
до інтеграла в полярних
координатах
![]() ,
, ![]() ,
які пов’язані з прямокутними координатами
співвідношеннями
,
які пов’язані з прямокутними координатами
співвідношеннями
![]() ,
,
![]() ,
(5.1.3)
,
(5.1.3)
здійснюється за формулою:
 .
(5.1.4)
.
(5.1.4)
Якщо
область
![]() обмежена променями, які утворюють з
полярною віссю кути
обмежена променями, які утворюють з
полярною віссю кути
![]() і
і
![]()
![]() ,
і кривими
,
і кривими
![]() і
і
![]()
![]() ,
то відповідні полярні координати
змінюються в межах області
,
то відповідні полярні координати
змінюються в межах області
![]() ,
і тоді
,
і тоді
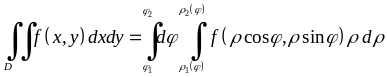 .
(5.1.5)
.
(5.1.5)
Приклад
5.1.1. Обчислити
інтеграл
 ,
де
‑ чверть круга
,
де
‑ чверть круга
![]() ,
що лежить в першій координатній чверті
,
що лежить в першій координатній чверті
![]() .
.
Розв’язання. У відповідності з формулами (5.1.4), (5.1.5):
 .
.
Площа плоскої фігури виражається формулою
 .
(5.1.6)
.
(5.1.6)
Об’єм
циліндричного тіла
(обмеженого зверху неперервною поверхнею
![]() ,
знизу – площиною
,
знизу – площиною
![]() і з боків – циліндричною поверхнею з
твірними, паралельними осі
і з боків – циліндричною поверхнею з
твірними, паралельними осі
![]() ),
що вирізає на площині
),
що вирізає на площині
![]() область
,
обчислюється за формулою:
область
,
обчислюється за формулою:
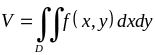 .
(5.1.7)
.
(5.1.7)
Якщо
пластинка займає область
площини
і має змінну поверхневу густину
![]() ,
то маса
пластинки
виражається подвійним інтегралом
,
то маса
пластинки
виражається подвійним інтегралом
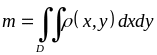 .
(5.1.8)
.
(5.1.8)
Координати центра мас обчислюються за формулами:
 ,
,
![]() ,
(5.1.9)
,
(5.1.9)
де
![]() ,
,
![]() .
.
Якщо
область інтегрування
![]() визначається нерівностями
визначається нерівностями
![]() ,
,
![]() ,
,
![]() ,
де
,
де
![]() ,
,
![]() ,
,
![]() ,
,
![]() – неперервні функції, то потрійний
інтеграл від
функції
– неперервні функції, то потрійний
інтеграл від
функції
![]() по області
,
обчислюється за формулою:
по області
,
обчислюється за формулою:
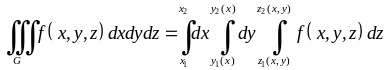 .
(5.1.10)
.
(5.1.10)
Об’єм просторового тіла, що займає область , визначається за формулою:
 .
(5.1.11)
.
(5.1.11)
Якщо
– деяка область простору, яку займає
матеріальне тіло з густиною
![]() ,
то маса
тіла
визначається формулою:
,
то маса
тіла
визначається формулою:
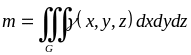 .
(5.1.12)
.
(5.1.12)
Приклад
5.1.2. Для
фігури
,
що обмежена лініями, вказаними в прикладі
3.3.1: а) записати подвійний інтеграл
![]() (
(![]() ‑ неперервна функція в
)
у вигляді повторного інтеграла та
змінити порядок інтегрування;
б) знайти
масу пластини
,
якщо густина
маси
‑ неперервна функція в
)
у вигляді повторного інтеграла та
змінити порядок інтегрування;
б) знайти
масу пластини
,
якщо густина
маси
![]() ;
в) обчислити
об’єм циліндричного тіла
;
в) обчислити
об’єм циліндричного тіла
![]() ,
обмеженого зверху площиною
,
обмеженого зверху площиною
![]() ,
знизу – площиною
і з боків – прямою циліндричною поверхнею,
що вирізає на площині
область
;
г) знайти
масу циліндричного тіла
,
якщо густина маси
,
знизу – площиною
і з боків – прямою циліндричною поверхнею,
що вирізає на площині
область
;
г) знайти
масу циліндричного тіла
,
якщо густина маси
![]() .
.
Розв’язання.
а) Криволінійна
трапеція
(див. рис. 3.3.1) обмежена
зверху –
параболою
,
знизу ‑ віссю
та проектується на відрізок
осі
.
Значить,
![]() є стандартною відносно вісі
.
є стандартною відносно вісі
.
З
іншого боку,
обмежена
зліва –
віткою параболи
![]() ,
справа – віткою параболи
,
справа – віткою параболи
![]() та проектується на відрізок
та проектується на відрізок
![]() осі
.
Таким чином,
осі
.
Таким чином,
![]() є стандартною відносно вісі
.
є стандартною відносно вісі
.
Отже, запишемо подвійний інтеграл у вигляді обох повторних за формулами (5.1.1), (5.1.2):
 .
.
б) Знайдемо
масу пластини
за формулою (5.1.8)
(де густина
маси
):
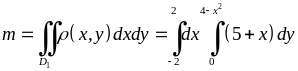 .
Спочатку обчислимо за змінною
“внутрішній” інтеграл, в якому
вважається сталим:
.
Спочатку обчислимо за змінною
“внутрішній” інтеграл, в якому
вважається сталим:
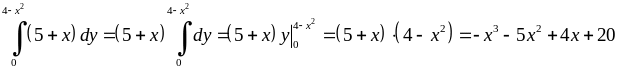 .
.
Тоді
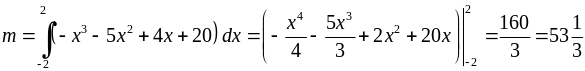 .
.
в) Об’єм
циліндричного тіла (обмеженого зверху
площиною
![]() )
згідно (5.1.7):
)
згідно (5.1.7):
 .
“Внутрішній” інтеграл
.
“Внутрішній” інтеграл

![]() .
.
Значить,
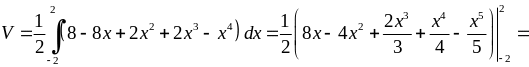
![]() (куб. од.)
(куб. од.)
г) Знайдемо масу циліндричного тіла за формулою (5.1.12):
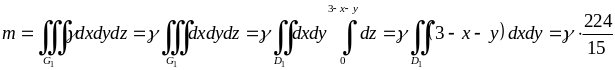 .
.
Зауважимо, що приклад 5.1.2 відповідає завданню 5.1 контрольної роботи.
Література: [1, с. 470 ‑ 492], [2, с. 581 ‑ 616], [3, с. 494 – 499], [13].
