8.3. Неперервні випадкові величини

Неперервною називається випадкова величина, що може приймати будь-які значення з деякого проміжку. Інтегральна функція неперервної випадкової величини є неперервною функцією. Неперервні випадкові величини можна задавати також за допомогою диференціальної функції. Диференціальною функцією або щільністю розподілу (щільністю ймовірностей) називається похідна від інтегральної функції:

(8.3.1)

Властивості диференціальної функції розподілу:

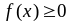• , (8.3.2)

• , (8.3.3)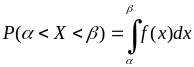

• , (8.3.4)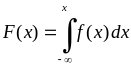

• (8.3.5)

(зв'язок між диференціальною й інтегральною функціями).

Математичним сподіванням неперервної випадкової величини називається невласний інтеграл

, (8.3.6)

де – диференціальна функція. Якщо випадкова величина , то .

Дисперсію неперервної випадкової величини можна обчислити за формулою:

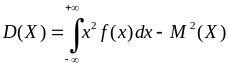, (8.3.7)

причому якщо , то .

Приклад 8.3.1. Інтегральну функцію розподілу ймовірностей неперервної випадкової величини задано формулою:

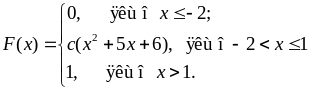
Знайти: а)  коефіцієнт с, б)  диференціальну функцію , в)   , , , г)  ймовірність попадання випадкової величини в інтервал ; д)  побудувати графіки функцій і .

Розв’язання. а), б)  Знайдемо диференціальну функцію за формулою (8.3.1):

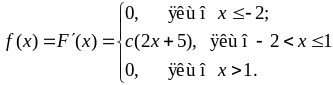
Коефіцієнт с визначаємо з умови (8.3.3), тобто , значить, , отже інтегральна і диференціальна функції набувають вигляду: , .

в)  Знайдемо математичне сподівання випадкової величини та випадкової величини за формулою (8.3.6):

.

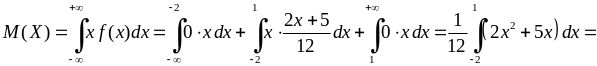
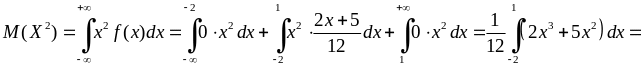
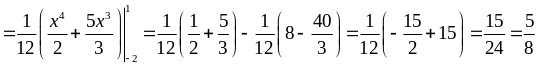Тоді дисперсія за формулою (8.2.9) , середнє квадратичне відхилення за (8.2.14): .

г)  ймовірність попадання випадкової величини в інтервал знайдемо за допомогою інтегральної функції й формули (8.2.4):

.

Цю ж ймовірність можна обчислити за допомогою диференціальної функції й формули (8.3.4): .

д)  графіки диференціальної й інтегральної функції мають вигляд:

Рис. 8.3.1 – Графік диференціальної функції

Рис. 8.3.2 – Графік інтегральної функції розподілу

Література: [1, с. 526 ‑ 529], [4, с. 529 – 559], [16], [18], [20].

8.4. Біноміальний та пуассонів закони розподілу

Біноміальним називається розподіл імовірностей дискретної випадкової величини за формулою Бернуллі. Для такої випадкової величини

, , . (8.4.1)

Приклад 8.4.1 Знайти математичне сподівання й дисперсію випадкової величини – числа людей, які можуть звернутися до консультанта (з приклада 8.2.1)

Розв’язання. Безпосередній підрахунок числових характеристик цієї випадкової величини, що є біноміально розподіленою, було виконано у прикладі 8.2.1 З іншого боку, , , і тому згідно (8.4.1): , .

Розподілом Пуассона називається розподіл імовірностей дискретної випадкової величини за формулою Пуассона. Для такої випадкової величини

, (де ). (8.4.2)

Закон Пуассона називають також законом рідких подій, він апроксимує біноміальний розподіл при досить великих і малих .

Приклад 8.4.2. Прилад містить 2500 мікроелементів, які працюють незалежно друг від друга. Імовірність того, що мікроелемент вийде з ладу під час роботи приладу, дорівнює 0,003. Знайти математичне сподівання, дисперсію й середнє квадратичне відхилення випадкової величини – числа мікроелементів, які вийдуть із ладу під час роботи приладу.

Розв’язання. Випадкова величина розподілена за законом Пуассона з параметром . Обчислимо її числові характеристики: згідно (8.4.2) , і за формулою (8.2.14) .

Література: [4, с. 563 – 564], [16], [18], [20].