8.5. Нормальний, рівномірний та показниковий закони

розподілу ймовірностей.

Нормальним називається розподіл імовірностей неперервної випадкової величини, диференціальна функція якої має вигляд: , де параметр – математичне сподівання, параметр – середнє квадратичне відхилення. Графік щільності ймовірності нормального розподілу називають нормальною кривою (кривою Гаусса):

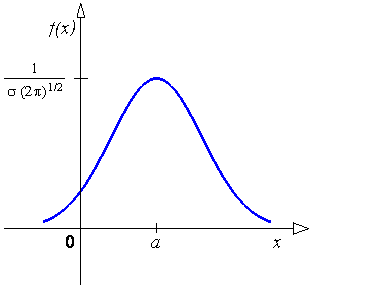
Рис. 8.5.1 – Крива Гаусса

Імовірність того, що нормальна випадкова величина прийме значення з інтервалу :

, (8.5.1)

де – функція Лапласа (табульована у додатку Б).

Імовірність того, що відхилення нормально розподіленої випадкової величини від її математичного сподівання за абсолютною величиною менше заданого додатного числа :

(8.5.2)

Правило “трьох сигм” Практично достовірною є подія, що полягає у тому, що абсолютна величина відхилення нормально розподіленої випадкової величини від її математичного сподівання не перевищує потроєного середнього квадратичного відхилення:

(8.5.3)

Нормальний закон проявляється в усіх тих випадках, коли випадкова величина є результатом дії великого числа різних факторів. Прикладами випадкових величин, що мають нормальний розподіл, можуть бути: відхилення від номінальних розмірів деталей, оброблених на станку, помилки при вимірюваннях, відхилення від цілі при стрільбі і т.д.

Приклад 8.5.1. Вага виробу має нормальний закон з  г і  г. Знайти ймовірності того, що: а)  вага виробу не менша 2990 г і не більша 3005 г; б)  вага виробу відхиляється від середнього значення   не більше ніж на 15 г.

Розв’язання. Випадкова величина – вага виробу є нормально розподіленою, тому маємо:

а)  за формулою (8.5.1) ( , ):

.

За таблицею (додаток Б) знаходимо: , , значить, .

б)  при  г за формулою (8.5.2):

.

Рівномірним називається розподіл імовірностей неперервної випадкової величини, всі значення якої належать відрізку , а диференціальна функція зберігає стале значення на . Диференціальна та інтегральна функції рівномірного розподілу мають вигляд:

. (8.5.4)

Графіки цих функцій:

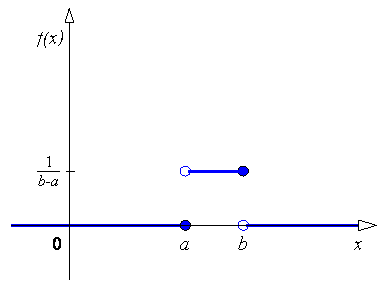
Рис. 8.5.2 – Диференціальна функція рівномірного розподілу

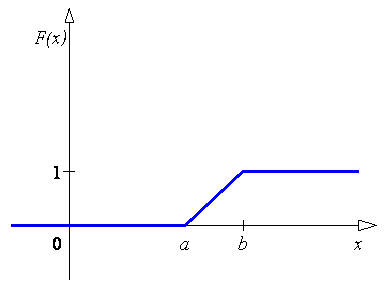
Рис. 8.5.3 –Інтегральна функція рівномірного розподілу

Числові характеристики (математичне сподівання, дисперсія):

, . (8.5.5)

Приклад 8.5.2. Потяги метрополітена йдуть строго за розкладом з інтервалом 2 хвилини. Час очікування потягу (пасажиром, який вийшов на платформу) є рівномірно розподіленою випадковою величиною . Знайти: а)  диференціальну та інтегральну функції; б)   , , .

Розв’язання. Випадкова величина – час очікування потягу – рівномірно розподілена на відрізку [0; 2]. Таким чином, у даному випадку , .

а)  Диференціальна та інтегральна функції цього рівномірного розподілу згідно (8.5.4) мають вигляд:

, .

б)  математичне сподівання, дисперсія та середнє квадратичне відхилення за формулами (8.5.5): , , та (8.2.14): .

Показниковий розподіл неперервної випадкової величини описується диференціальною та інтегральною функціями:

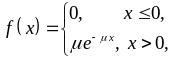
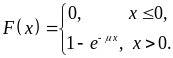(8.5.6)

де параметр розподілу .