Модуль 1 Системи рівнянь, вектори та аналітична геометрія

1.1. Визначники, матриці, розв’язання систем лінійних рівнянь

методами оберненої матриці, Крамера, Гаусса

Визначником (детермінантом) другого порядку називається число, яке обчислюється за формулою

. (1.1.1)

Приклад 1.1.1. Обчислити визначник .

Розв’язання. За формулою (1.1.1) маємо:

Визначником третього порядку називається число, яке визначається формулою

(1.1.2)

і обчислення якого можна ілюструвати за допомогою наступної схеми:

«+» «‑»

Рис. 1.1.1 ‑ Правило трикутника

Таким чином, у суму (1.1.2) зі своїм знаком входять добутки елементів, розташованих на головній діагоналі ( ) та на відповідних трикутниках (паралелі до головної діагоналі з’єднуються з протилежним кутом таблиці), а з протилежним знаком ‑ добутки елементів, розташованих на побічній діагоналі та на відповідних трикутниках (паралелі до побічної діагоналі з’єднуються з протилежним кутом).

Приклад 1.1.2. Обчислити визначник .

Розв’язання. За формулою (1.1.2) маємо:

.

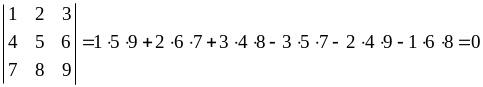Мінором елемента називається визначник, який утворюється з даного викреслюванням i-го рядка і j-го стовпчика, на яких розташований елемент . Алгебраїчним доповненням елемента називається мінор, помножений на . Отже, .

Приклад 1.1.3. Знайти для визначника з прикладу 1.1.2.

Розв’язання. .

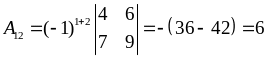Матрицею називається таблиця чисел. Матриця має розмірність (n´m), де n – кількість рядків, m – кількість стовпчиків. Якщо , матриця називається квадратною.

На головній діагоналі квадратної матриці розташовані елементи , для яких номер рядка та стовпчика співпадають. Якщо всі елементи нижче (вище) головної діагоналі квадратної матриці дорівнюють нулю, то матриця називається трикутною.

Якщо визначник (позначення: ) квадратної матриці не дорівнює нулю, то матриця називається невиродженою.

Транспонованою матрицею називається матриця, у якої рядки записані замість стовпчиків (стовпчики ‑ замість рядків).

Сумою двох матриць і однакової розмірності називається матриця , елементи якої дорівнюють сумі відповідних елементів матриць і .

Добутком матриці на число k називається матриця, елементами якої є .

Добутком матриці розмірності (n´k) на матрицю розмірності (k´m) називається матриця розмірності (n´m), кожний елемент якої дорівнює скалярному добутку (див. формулу (1.2.4)) -го вектора‑рядка матриці на -й вектор‑стовпчик матриці .

Приклад 1.1.4. 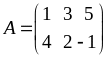, 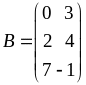. Знайти .

Розв’язання. Матриця розмірності , а матриця ‑ , отже буде мати розмірність (множити на не можна). .

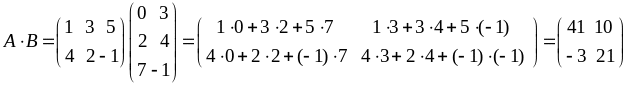Одиничною матрицею називається матриця, елементи головної діагоналі якої дорівнюють одиниці, а всі інші ‑ нулю.

Оберненою матрицею до невиродженої матриці називається матриця, для якої виконується рівність

. (1.1.3)

Матрицю (розмірності 3´3) можна знайти за формулою

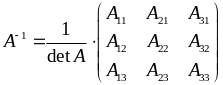. (1.1.4)

Розглянемо систему трьох лінійних рівнянь з трьома невідомими:

. (1.1.5)

Позначимо 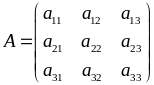‑ матриця системи, 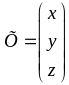‑ стовпчик невідомих, ‑ стовпчик вільних членів, тоді систему (1.1.5) можна записати в матричному виді:

. (1.1.6)

Якщо , то розв’язок системи (1.1.6) має вигляд:

, (1.1.7)

та може бути знайдений за методом оберненої матриці.

Якщо , то за формулами Крамера розв’язком (1.1.5) є:

, (1.1.8)

де ( , ) ‑ матриця, одержана із матриці заміною стовпця із коефіцієнтів при невідомому ( , ) стовпчиком вільних членів.

Метод Гаусса розв’язання системи складається з двох кроків: спочатку система шляхом виключень невідомих приводиться еквівалентними перетвореннями до трикутного виду (тобто матриця отриманої системи є трикутною). Зазначимо, що

• множення (або ділення) обох частин будь якого рівняння системи на число, що не дорівнює нулю;

• додавання (або віднімання) рівнянь

є еквівалентними перетвореннями системи, тобто не змінюють її розв’язку. Зауважимо, що метод Гаусса є застосовним не лише для систем, матриця яких є квадратною.

Приклад 1.1.1. Розв’язати систему 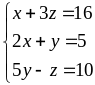методом оберненої матриці.

Розв’язання. Матриця системи (із коефіцієнтів при невідомих) 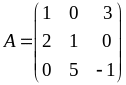, її визначник . Значить, матриця має обернену.

Для побудови запишемо спочатку алгебраїчні доповнення:

, , ,

, , , , , .

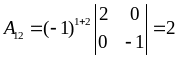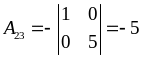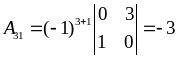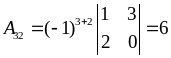Тоді за формулою (1.1.4) обернена матриця .

Значить, згідно формули (1.1.7)

.

Отже, .

Приклад 1.1.2. Розв’язати систему методом Крамера.

Розв’язання. Матриця системи (із коефіцієнтів при невідомих) , її визначник . Значить, систему можна розв’язати за методом Крамера.

Допоміжні визначники:

, , .

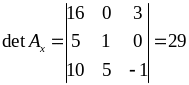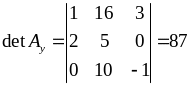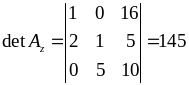Тоді за формулами Крамера .

Отже, .

Приклад 1.1.3. Розв’язати систему методом Гаусса.

Розв’язання. Розв’яжемо систему методом Гаусса. Перше рівняння запишемо без змін. З усіх інших рівнянь виключимо невідому . (Без змін можна записати будь-яке рівняння системи і обрати для виключення з усіх інших рівнянь будь-яку невідому, що входить в це рівняння з ненульовим коефіцієнтом). Якщо помножити перше рівняння на (-2) і додати до другого рівняння: , то після цього перетворення друге рівняння матиме вигляд: . Третє рівняння вже не містить . (Інакше ми б помножили перше та третє рівняння на такі числа, щоб додавання отриманих рівнянь призвело до зникнення ). Отримали систему .

Тепер перше та друге рівняння запишемо без змін, а з третього рівняння виключимо невідому . Для цього помножимо друге рівняння на (-5) і додамо до третього рівняння: . Отримаємо третє рівняння вже без невідомої : . Таким чином, ми шляхом елементарних перетворень призвели систему до еквівалентного трикутного виду: .

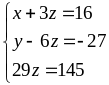З останнього рівняння, яке містить лише одну змінну, знаходимо , потім із передостаннього . Підставляючи знайдені значення в перше рівняння, маємо .

Отже, .

Зауважимо, що приклади  1.1.1 ‑ 1.1.3 відповідають завданню  1.1 контрольної роботи.

Література: [1, с. 281 ‑ 294], [2, с. 383 ‑ 389], [3, с. 23 – 35, 64 ‑ 81], [5], [6].