Модуль 3. Невизначений і визначений інтеграли
3.1. Знайти невизначені та визначені інтеграли:
а) методом безпосереднього інтегрування,
б) методом заміни змінної (підстановки),
в) інтегруванням частинами,
г) від раціональної або ірраціональної функції шляхом виділення
повного квадрату у знаменнику,
д) способом перетворення добутків тригонометричних функцій у
суми.
3.1.1. |
а) б) в) г) д) |
3.1.2. |
а) б) в) г) д) |
3.1.3. |
а) б) в) г) д) |
3.1.4. |
а) б) в) г) д) |
3.1.5. |
а) б) в) г) д) |
3.1.6. |
а) б) в) г) д) |
3.1.7. |
а) б) в) г) д) |
3.1.8. |
а) б) в) г) д) |
3.1.9. |
а) б) в) г) д) |
3.1.10. |
а) б) в) г) д) |
3.1.11. |
а) б) в) г) д) |
3.1.12. |
а) б) в) г) д) |
3.1.13. |
а) б) в) г) д) |
3.1.14. |
а) б) в) г) д) |
3.1.15. |
а) б) в) г) д) |
3.1.16. |
а) б) в) г) д) |
3.1.17. |
а) б) в) г) д) |
3.1.18. |
а) , б) в) г) д) |
3.1.19. |
а) б) в) г) д) |
3.1.20. |
а) б) в) г) д) |
3.1.21. |
а) б) в) г) д) |
3.1.22. |
а) б) в) г) д) |
3.1.23. |
а) б) в) , г) д) |
3.1.24. |
а) б) в) г) д) |
3.1.25. |
а) б) в) г) д) |
3.1.26. |
а) б) в) г) д) |
3.1.27. |
а) б) в) г) д) |
3.1.28. |
а) б) в) г) д) |
3.1.29. |
а) б) в) г) д) |
3.1.30. |
а) б) в) г) д) |
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
,
,
,
,
.
3.2. Дослідити на збіжність невласний інтеграл.
3.2.1.
|
3.2.2.
|
3.2.3.
|
3.2.4.
|
3.2.5.
|
3.2.6.
|
3.2.7.
|
3.2.8.
|
3.2.9.
|
3.2.10.
|
3.2.11.
|
3.2.12.
|
3.2.13.
|
3.2.14.
|
3.2.15.
|
3.2.16.
|
3.2.17.
|
3.2.18.
|
3.2.19.
|
3.2.20.
|
3.2.21.
|
3.2.22. |
3.2.23.
|
3.2.24.
|
3.2.25. |
3.2.26.
|
3.2.27.
|
3.2.28.
|
3.2.29.
|
3.2.30.
|
3.3.
За допомогою інтегрального числення
для обмеженої заданими лініями плоскої
фігури
:
обчислити площу,
знайти координати центра ваги, якщо густина маси
,обчислити об’єм тіла, що утворюється при обертанні фігури навколо вісі
.
3.3.1.
|
3.3.2.
|
3.3.3.
|
3.3.4.
|
3.3.5.
|
3.3.6.
|
3.3.7.
|
3.3.8.
|
3.3.9.
|
3.3.10.
|
3.3.11.
|
3.3.12.
|
3.3.13.
|
3.3.14.
|
3.3.15.
|
3.3.16.
|
3.3.17.
|
3.3.18.
|
3.3.19.
|
3.3.20.
|
3.3.21.
|
3.3.22.
|
3.3.23.
|
3.3.24.
|
3.3.25.
|
3.3.26.
|
3.3.27.
|
3.3.28.
|
3.3.29.
|
3.3.30.
|
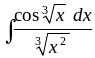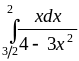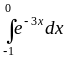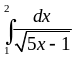