
Алгебраїчні доповнення.
Визначення. Алгебраїчним доповненням мінору матриці називається його додатковий мінор, помножений на (-1) в ступені, що дорівнює сумі номерів рядків і номерів шпальт мінору матриці.
В окремому випадку, алгебраїчним доповненням елемента матриці називається його додатковий мінор, взятий зі своїм знаком, якщо сума номерів стовпця і рядка, на яких стоїть елемент, є число парне і з протилежним знаком, якщо непарне.
Теорема Лапласа. Якщо вибрано s рядків матриці з номерами i1, … ,is, то визначник цієї матриці дорівнює сумі добутків усіх мінорів, розташованих у вибраних рядках на їх алгебраїчні доповнення.
Зворотна матриця.
Визначимо операцію ділення матриць як операцію, зворотну множенню. Визначення. Якщо існують квадратні матриці Х і А одного порядку, що задовольняють умові: XA = AX = E,
де Е - одинична матриця того ж самого порядку, що й матриця А, то матриця Х називається оберненою до матриці А і позначається А-1.
Кожна квадратна матриця з визначником, не рівним нулю має зворотну матрицю і притому тільки одну.
Розглянемо загальний підхід до знаходження зворотної матриці. Виходячи з визначення добутку матриць, можна записати:
AX
= E
![]() ,
i=(1,n), j=(1,n),
,
i=(1,n), j=(1,n),
eij = 0, i j,
eij = 1, i = j .
Таким чином, ми отримуємо систему рівнянь:
![]()
Розв’язав цю систему, знаходимо елементи матриці Х:
Приклад.
Дана матриця А =
![]() ,
знайти А-1.
,
знайти А-1.
![]()
![]()
![]()
Таким
чином, А-1=![]() .
.
Проте, такий спосіб не зручний при знаходженні зворотних матриць великих порядків, тому зазвичай застосовують наступну формулу:
-
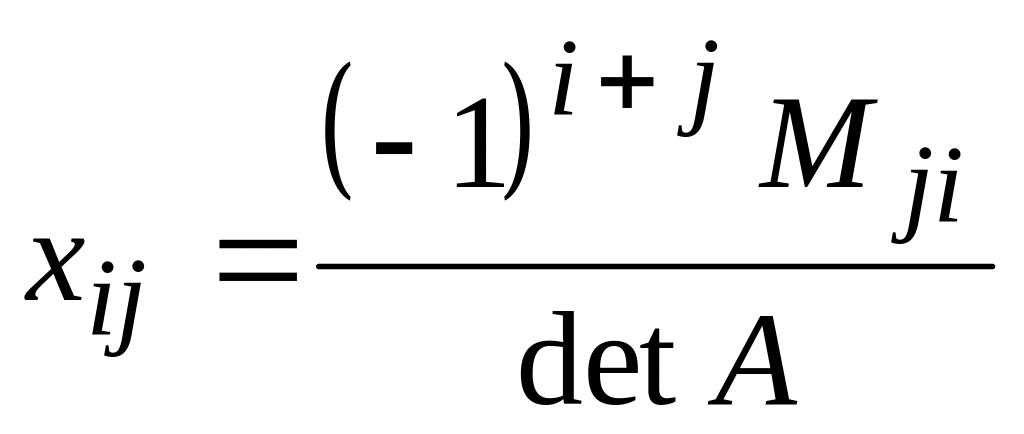 ,
,
де Мji- додатковий мінор елементу аji матриці А.
Приклад. Дана матриця А = , знайти А-1.
det A = 4 - 6 = -2.
M11=4; M12= 3; M21= 2; M22=1
x11= -2; x12= 1; x21= 3/2; x22= -1/2
Таким чином, А-1= .
Властивості зворотних матриць.
Зазначимо такі властивості зворотних матриць:
(A-1)-1 = A;
2) (AB)-1 = B-1A-1
3) (AT)-1 = (A-1)T.
Приклад.
Дана матриця А =
![]() ,
знайти А3.
,
знайти А3.
А2
= АА =
=
![]() ;
A3
=
=
;
A3
=
=
![]() .
.
Відзначимо, що матриці і є перестановочні.
Приклад.
Обчислити
визначник
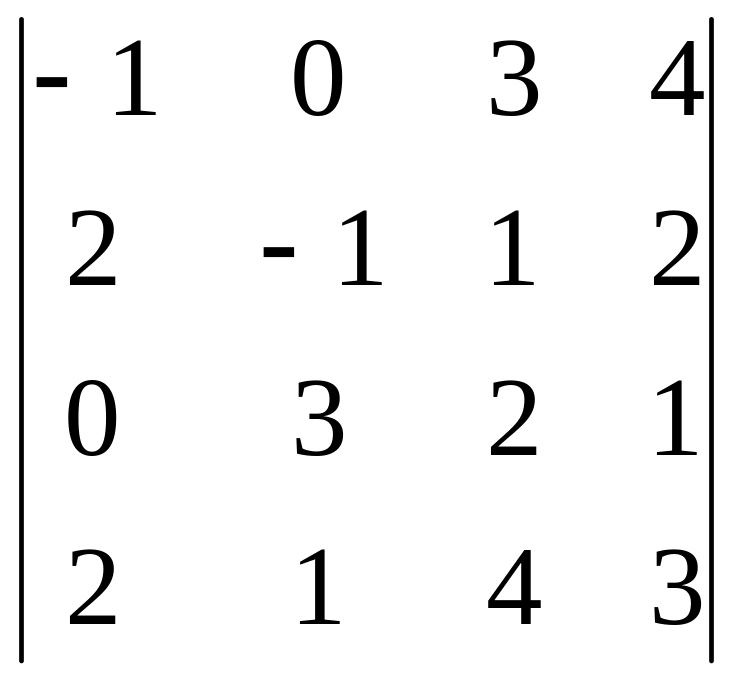 .
.
= -1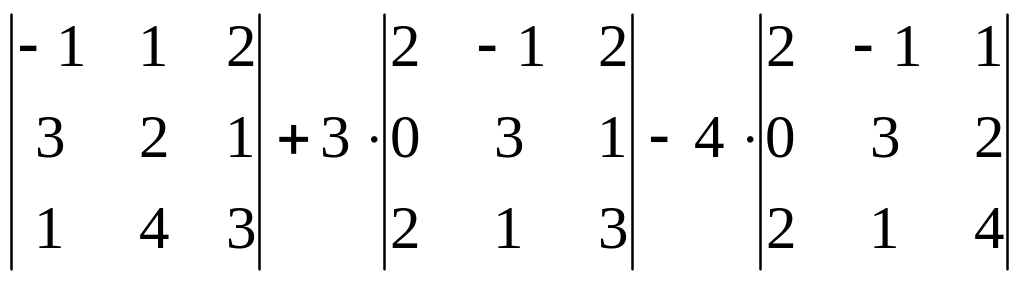
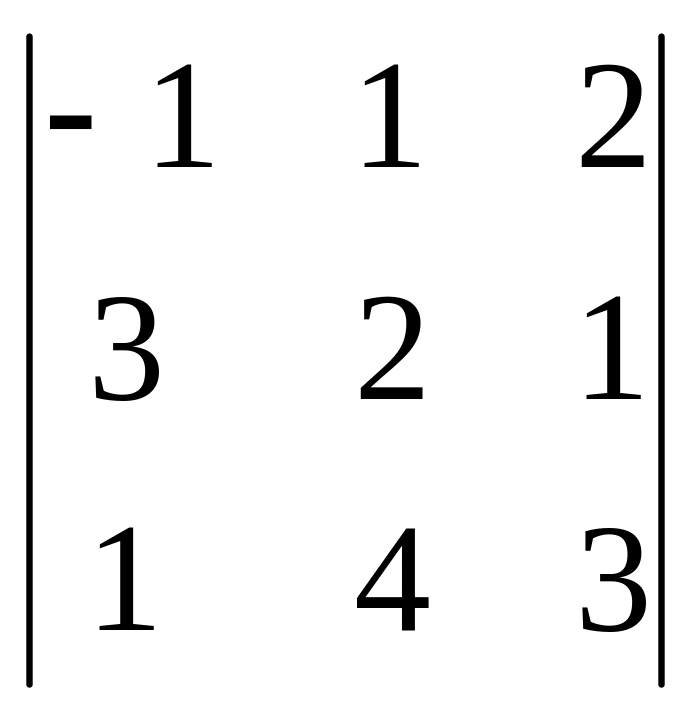 = -1(6 – 4) – 1(9 – 1) +
2(12 – 2) = -2 – 8 + 20 = 10.
= -1(6 – 4) – 1(9 – 1) +
2(12 – 2) = -2 – 8 + 20 = 10.
 =
=
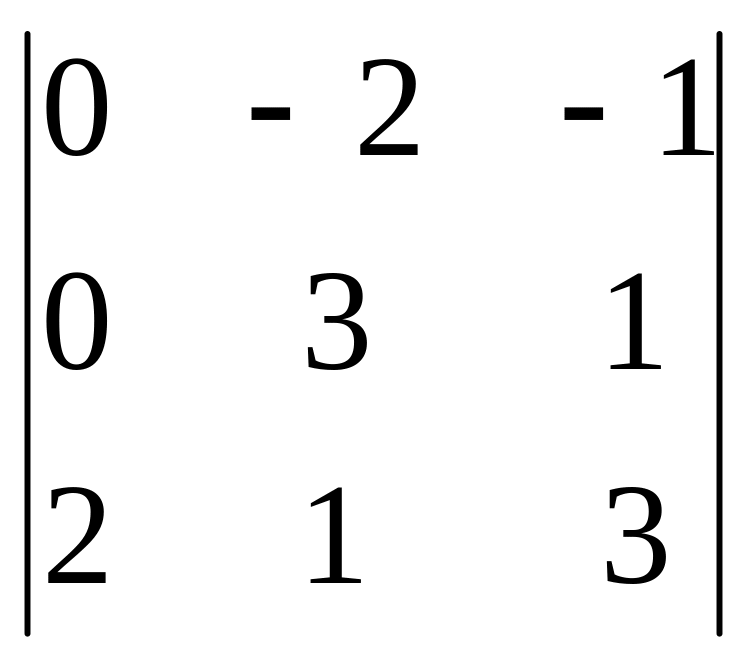 =
2(0 – 2) – 1(0 – 6) = 2.
=
2(0 – 2) – 1(0 – 6) = 2.
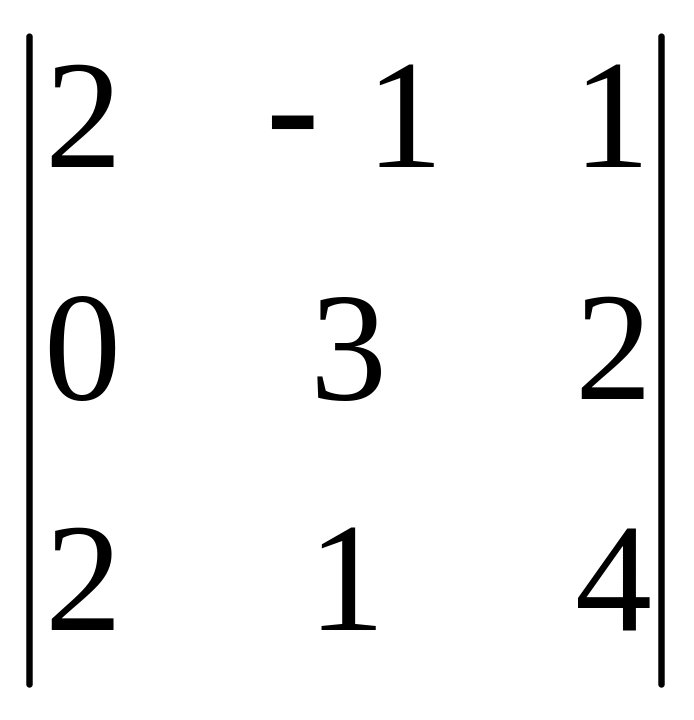 =
=
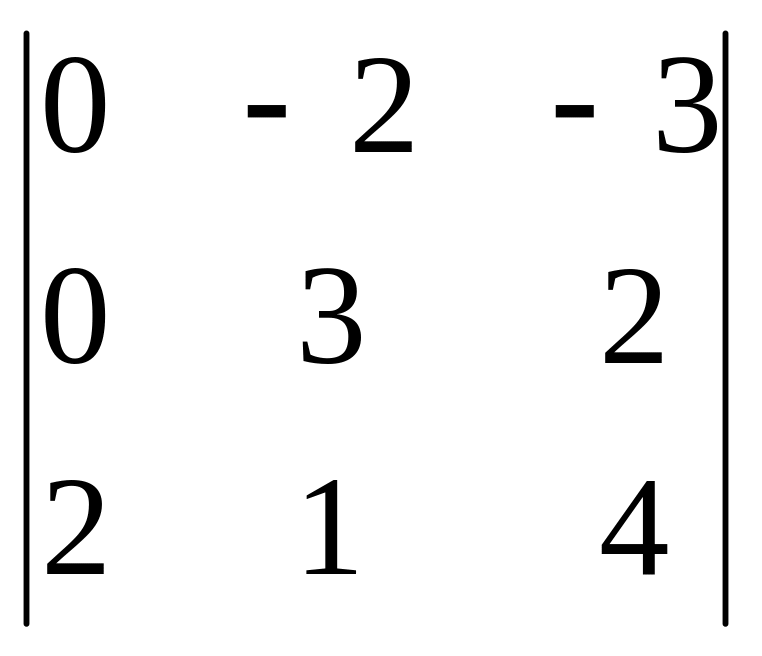 = 2(-4) – 3(-6) = -8 + 18 = 10.
= 2(-4) – 3(-6) = -8 + 18 = 10.
Значення визначника: -10 + 6 – 40 = -44.
Базисний мінор матриці. Ранг матриці.
Як було сказано вище, мінором матриці порядку s називається визначник матриці, утвореної з елементів вихідної матриці, що знаходяться на перетині будь - яких обраних s рядків і s стовпців. Визначення. У матриці порядку mn мінор порядку r називається базисним, якщо він не дорівнює нулю, а всі мінори порядку r +1 і вище дорівнюють нулю, або не існують зовсім, тобто r збігається з меншим із чисел m або n.
Стовпці і рядки матриці, на яких стоїть базисний мінор, також називаються базисними. У матриці може бути декілька різних базисних мінорів, що мають однаковий порядок. Визначення. Порядок базисного мінору матриці називається рангом матриці і позначається Rg А.
Дуже важливою властивістю елементарних перетворень матриць є те, що вони не змінюють ранг матриці.
Визначення. Матриці, отримані в результаті елементарного перетворення, називаються еквівалентними. Треба відзначити, що рівні матриці і еквівалентні матриці - поняття абсолютно різні. Теорема. Найбільше число лінійно незалежних стовпців в матриці дорівнює числу лінійно незалежних рядків.
Так як елементарні перетворення не змінюють ранг матриці, то можна істотно спростити процес знаходження рангу матриці.
Приклад. Визначити ранг матриці.
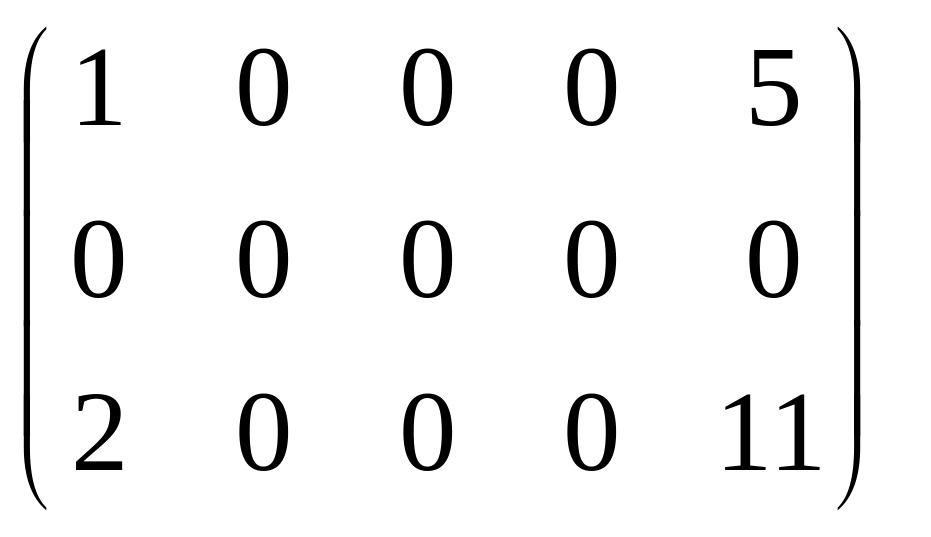
![]()
![]() ,
,
![]() RgA
= 2.
RgA
= 2.
Приклад. Визначити ранг матриці.
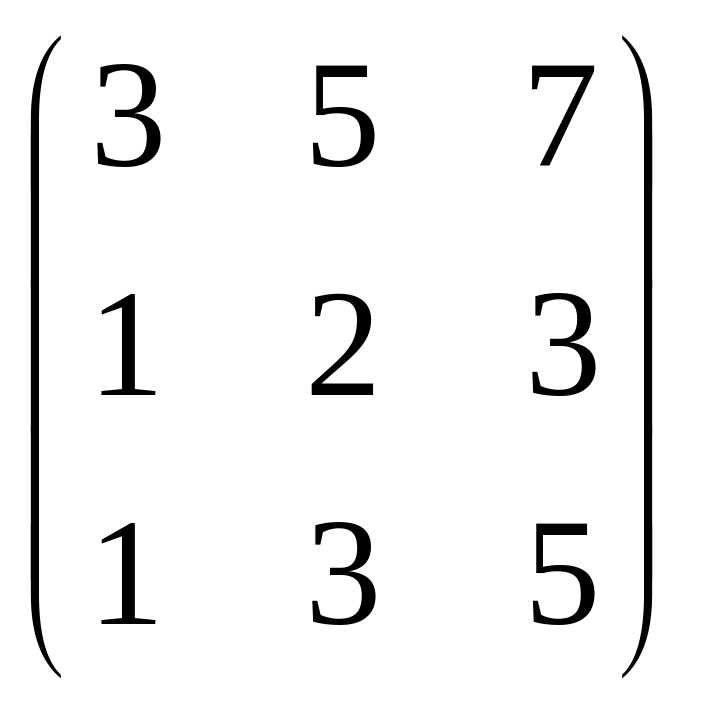
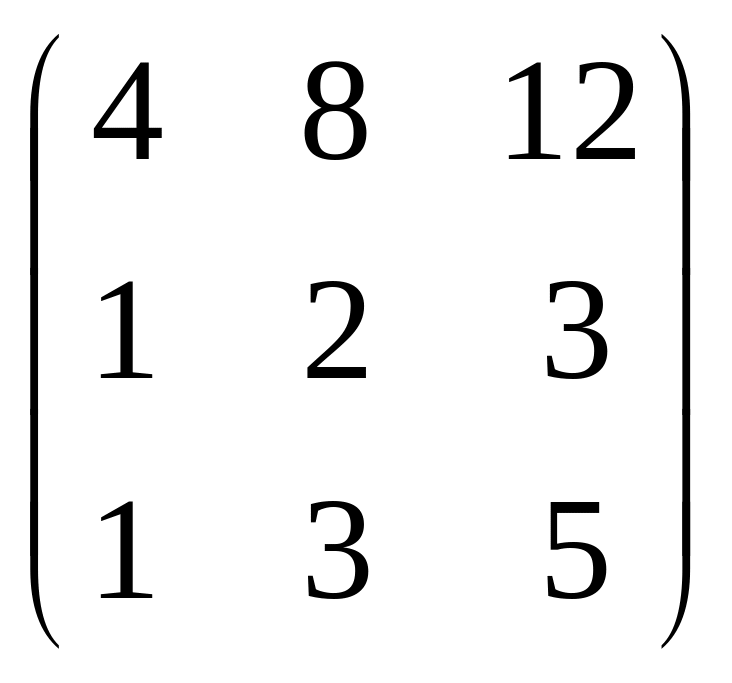
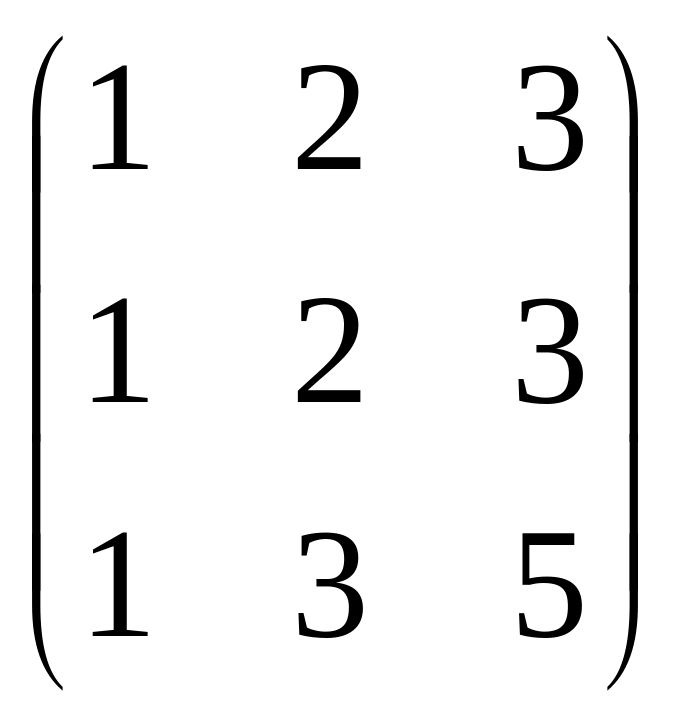
![]() ,
,
![]() Rg
= 2.
Rg
= 2.
Приклад. Визначити ранг матриці.
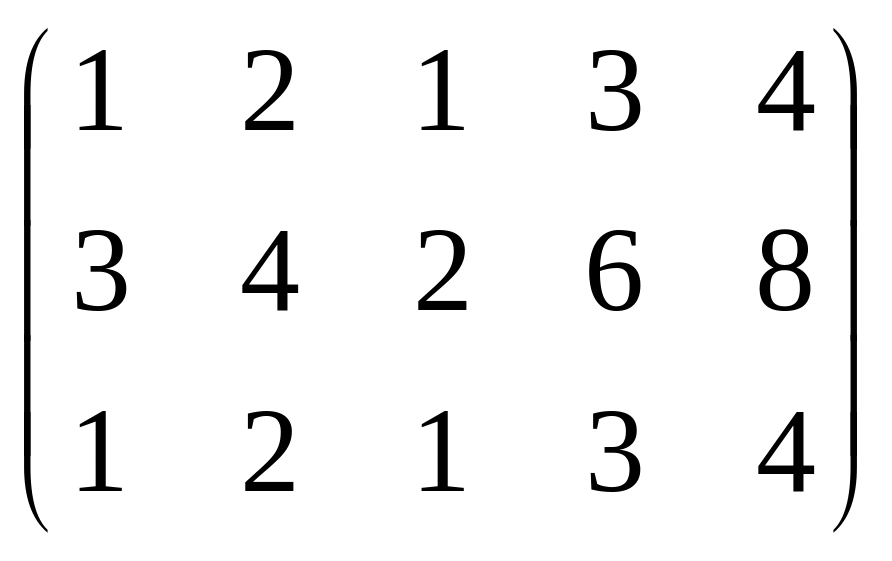
![]() ,
,
![]()
Rg
= 2.
Rg
= 2.
Якщо за допомогою елементарних перетворень не вдається знайти матрицю, еквівалентну вихідній, але меншого розміру, то знаходження рангу матриці слід починати з обчислення мінорів найвищого можливого порядку. У наведеному вище прикладі - це мінори порядку 3. Якщо хоча б один з них не дорівнює нулю, то ранг матриці дорівнює порядку цього мінору. Теорема про базисний мінор.
Теорема. У довільній матриці А кожен стовпець (рядок) є лінійною комбінацією стовпців (рядків), в яких розташований базисний мінор.
Таким чином, ранг довільної матриці А дорівнює максимальному числу лінійно незалежних рядків (стовпців) в матриці.
Якщо А-квадратна матриця і det A = 0, то по крайній мірі один зі стовпців - лінійна комбінація інших стовпців. Те ж саме справедливо і для рядків. Дане твердження випливає з властивості лінійної залежності при визначнику рівному нулю.
Матричний метод розв'язання систем лінійних рівнянь.
Матричний метод застосуємо до рішення систем рівнянь, де число рівнянь дорівнює числу невідомих.
Метод зручний для рішення систем невисокого порядку. Метод заснований на застосуванні властивостей множення матриць. Нехай дана система рівнянь:
![]()
Складемо
матриці: A
=
;
B
=
![]() ;
X
=
;
X
=
![]() .
.
Систему рівнянь можна записати:
AX = B.
Зробимо наступні перетворення: A-1AX = A-1B,
Так як А-1А = Е, то ЕХ = А-1В
Х = А-1В
Для застосування даного методу необхідно знаходити зворотну матрицю, що може бути пов'язано з обчислювальними труднощами при вирішенні систем вищого порядку.
Приклад. Розв’язати систему рівнянь:
![]()
Х
=
![]() ,
B
=
,
B
=
![]() ,
A
=
,
A
=
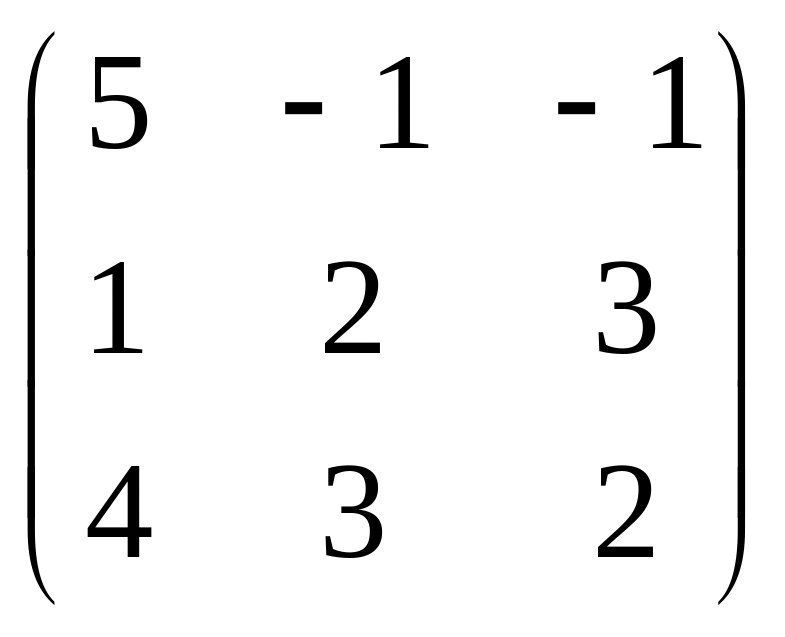
Знайдемо обернену матрицю А-1.
=
det A =
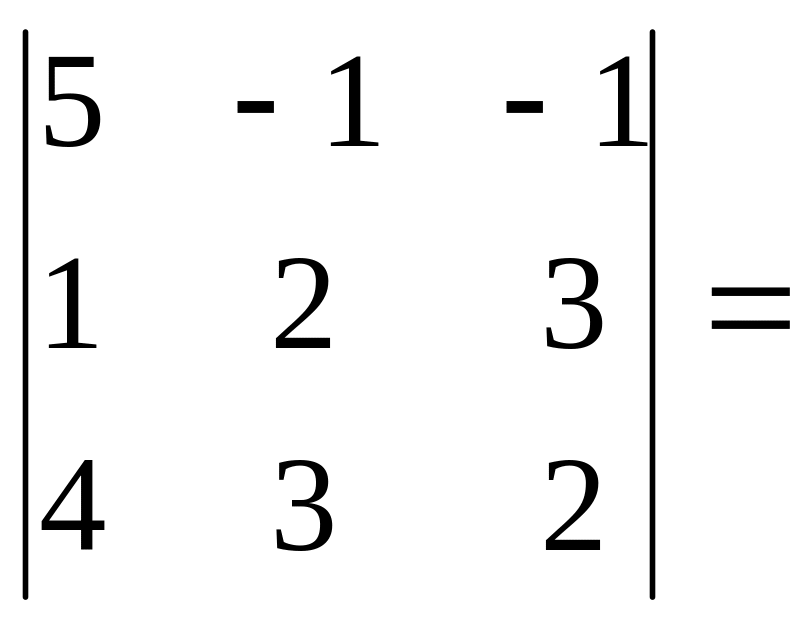 5(4-9)
+ 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
5(4-9)
+ 1(2 – 12) – 1(3 – 8) = -25 – 10 +5 = -30.
M11
=
![]() = -5; M21
=
= -5; M21
=
![]() = 1; M31
=
= 1; M31
=
![]() = -1;
= -1;
M12
=
![]() M22
=
M22
=
![]() M32
=
M32
=
![]()
M13
=
![]() M23
=
M23
=
![]() M33
=
M33
=
![]()
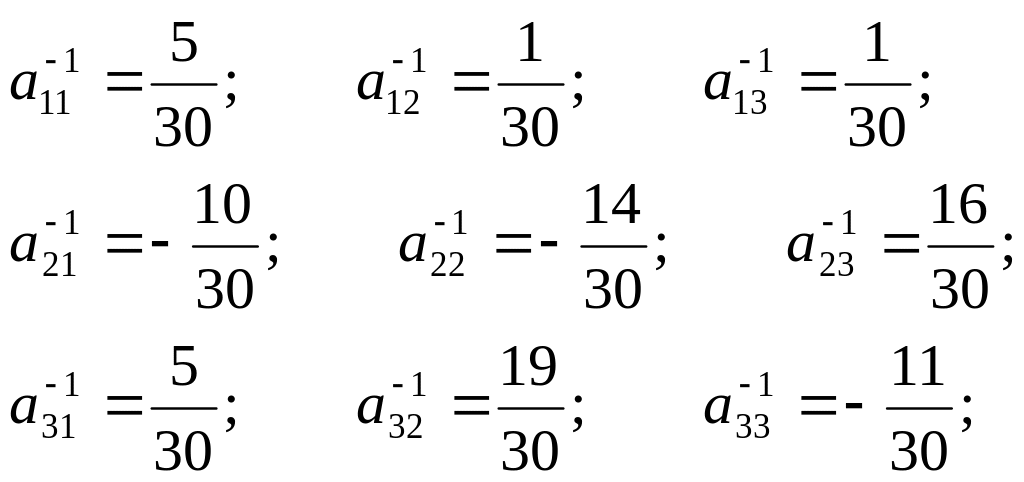 A-1
=
A-1
=
 ;
;
Зробимо перевірку:
AA-1
=
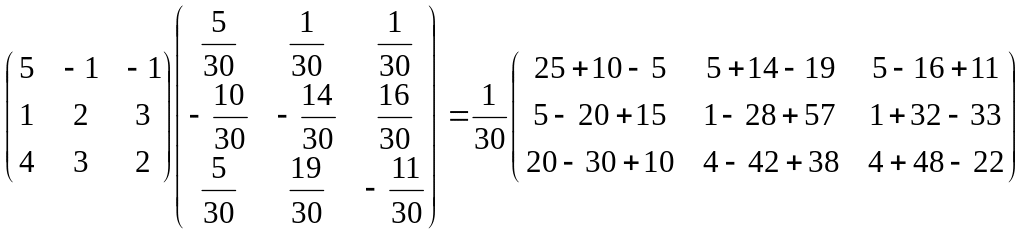 =E.
=E.
Знаходимо матрицю Х.
Х
=
=
А-1В
=
=
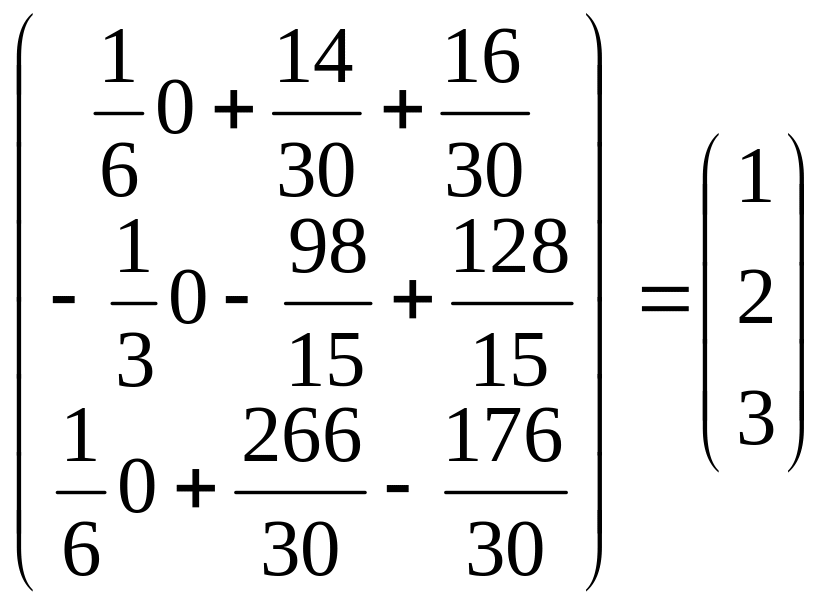 .
.
Разом рішення системи: x =1; y = 2; z = 3.
Незважаючи на обмеження можливості застосування даного методу і складність обчислень при великих значеннях коефіцієнтів, а також систем вищого порядку, метод може бути легко реалізований на ЕОМ.
Метод Крамера.
(Габріель Крамер (1704-1752) швейцарський математик)
Даний метод також застосовується лише в разі систем лінійних рівнянь, де число змінних співпадає з числом рівнянь. Крім того, необхідно ввести обмеження на коефіцієнти системи. Необхідно, щоб всі рівняння були лінійно незалежні, тобто жодне рівняння не було б лінійної комбінацією інших. Для цього необхідно, щоб визначник матриці системи не дорівнював 0. det A 0;
Дійсно, якщо яке-небудь рівняння системи є лінійна комбінація інших, то якщо до елементів будь-якої рядка додати елементи іншого, помножені на яке-небудь число, за допомогою лінійних перетворень можна отримати нульовий рядок. Визначник в цьому випадку буде дорівнює нулю.
Теорема. (Правило Крамера).
Теорема. Система з n рівнянь з n невідомими
![]()
у випадку, якщо визначник матриці системи не дорівнює нулю, має єдине рішення і це рішення знаходиться за формулами:
xi = i/, де
= det A, а i – визначник матриці, одержуваної з матриці системи заміною стовпця i стовпцем вільних членів bi.
i
=
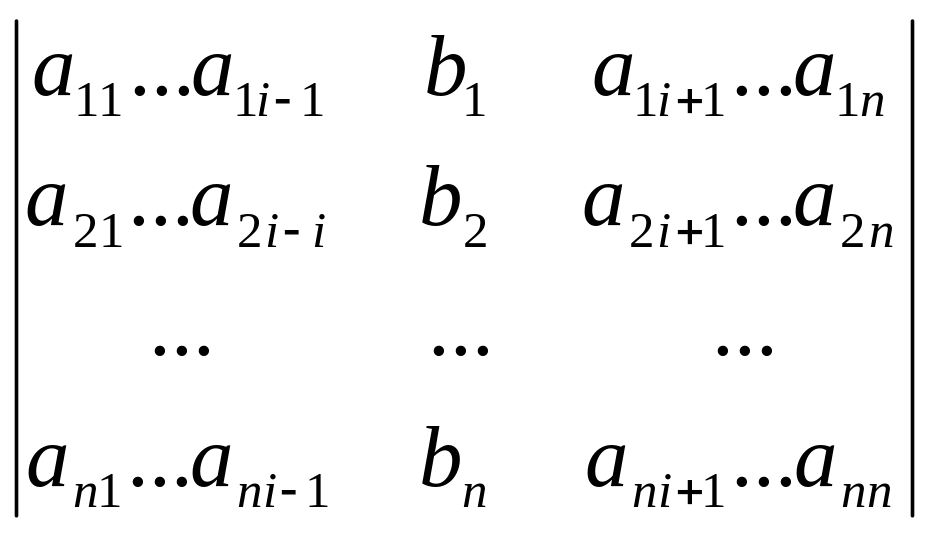
Приклад.
![]()
A
=
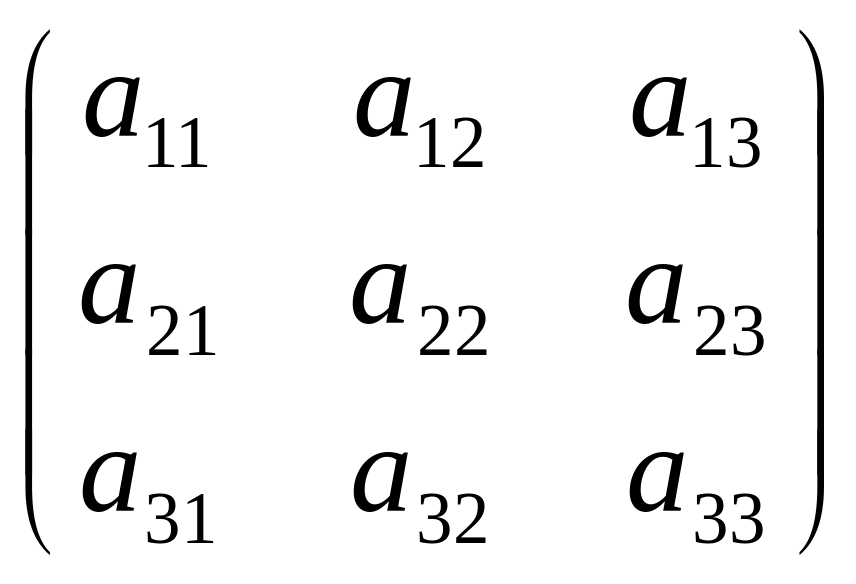 ;
1=
;
1=
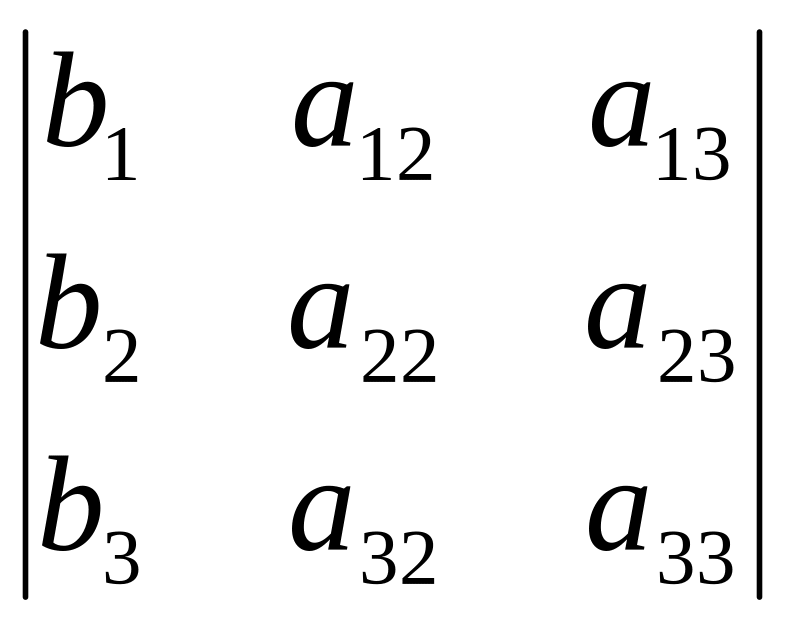 ;
2=
;
2=
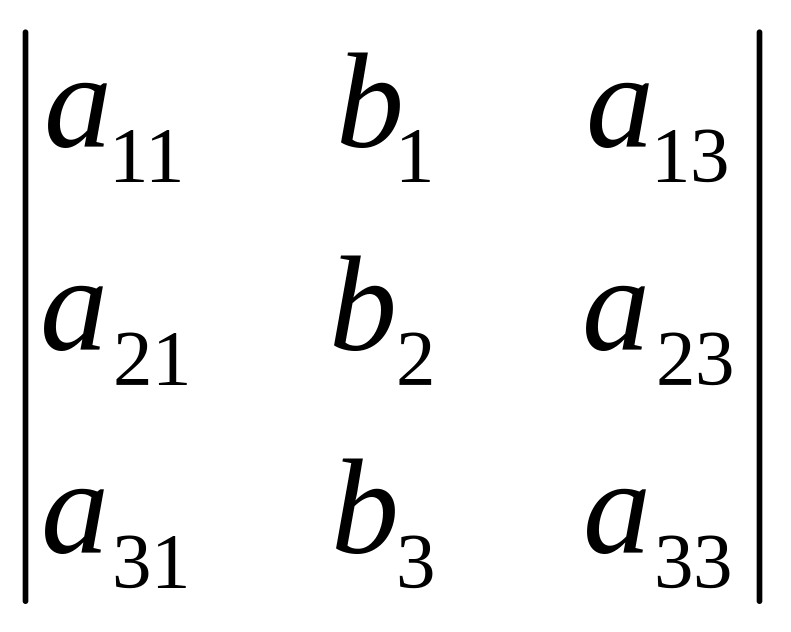 ;
3=
;
3=
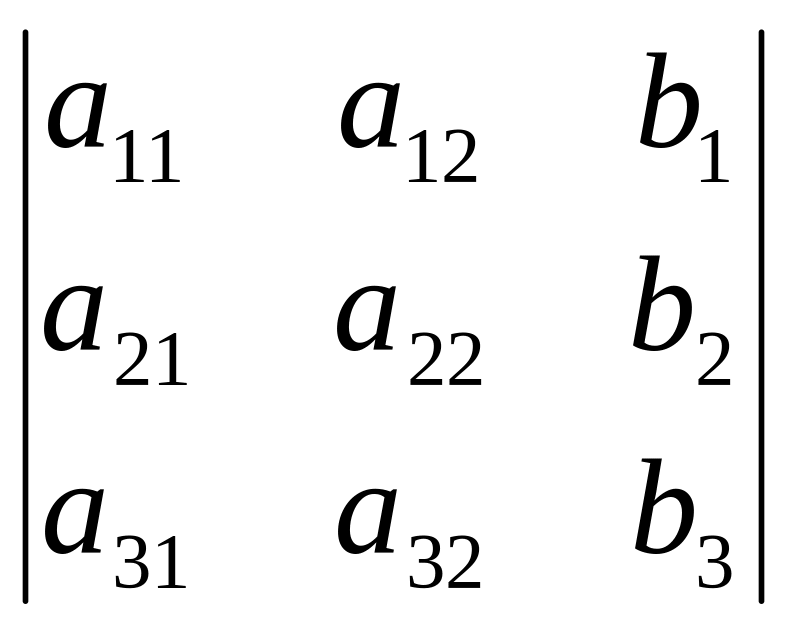 ;
;
x1 = 1/detA; x2 = 2/detA; x3 = 3/detA;
Приклад. Знайти розв’язання системи рівнянь:
=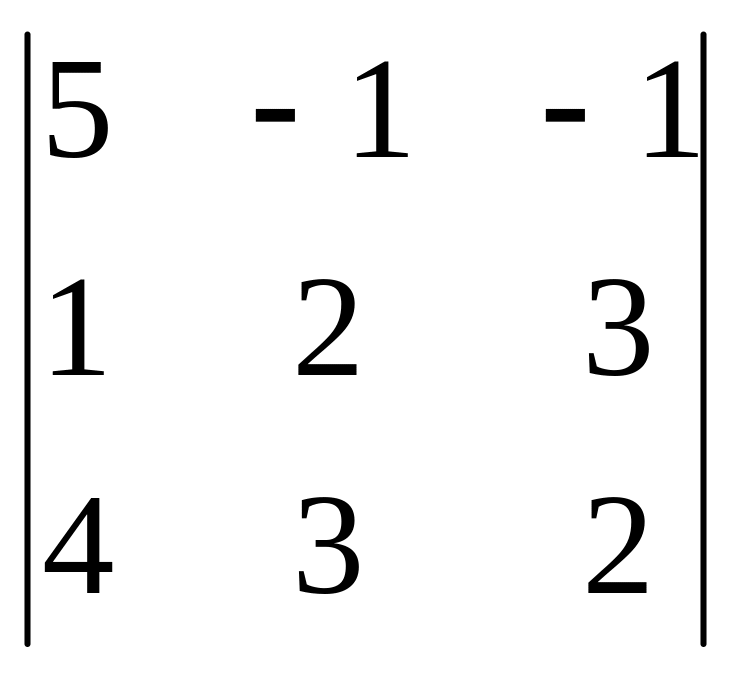 = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
1
=
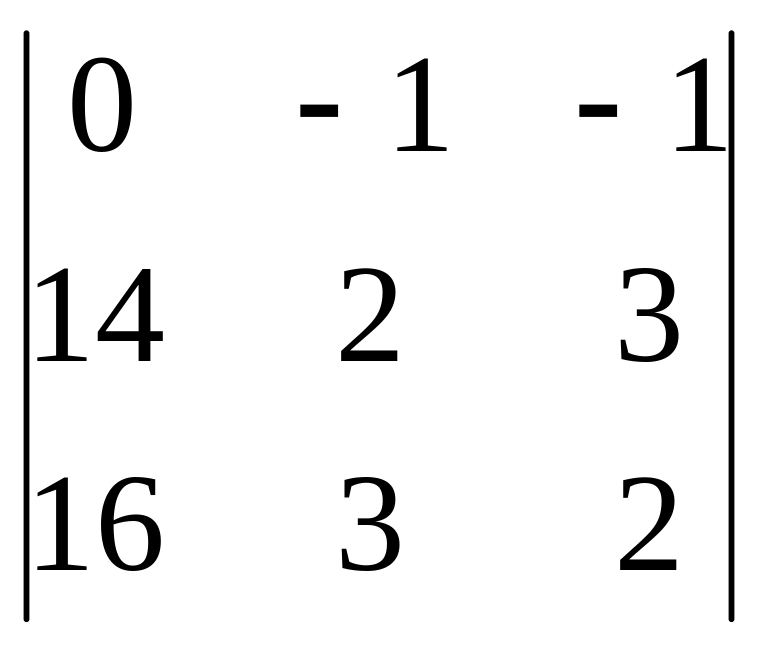 = (28 – 48) – (42 – 32) = -20 – 10 = -30.
= (28 – 48) – (42 – 32) = -20 – 10 = -30.
x1 = 1/ = 1;
2
=
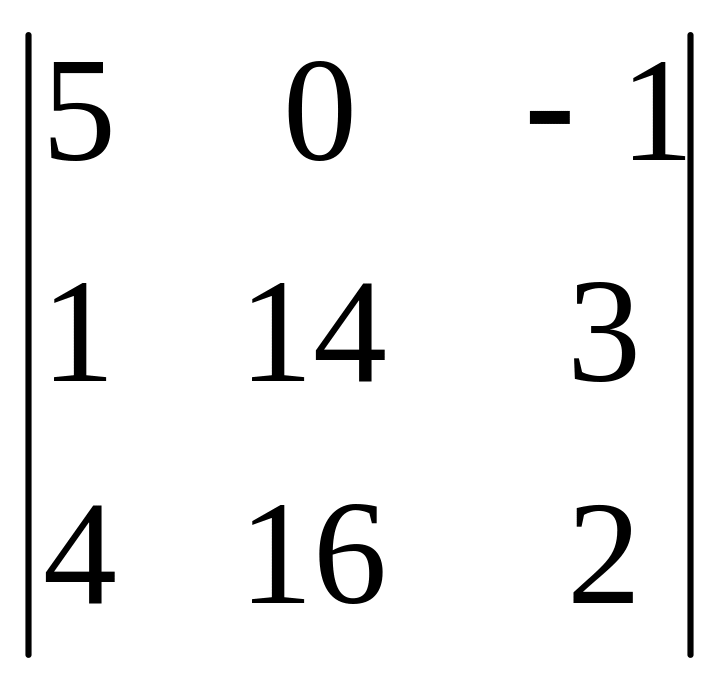 = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
x2 = 2/ = 2;
3
=
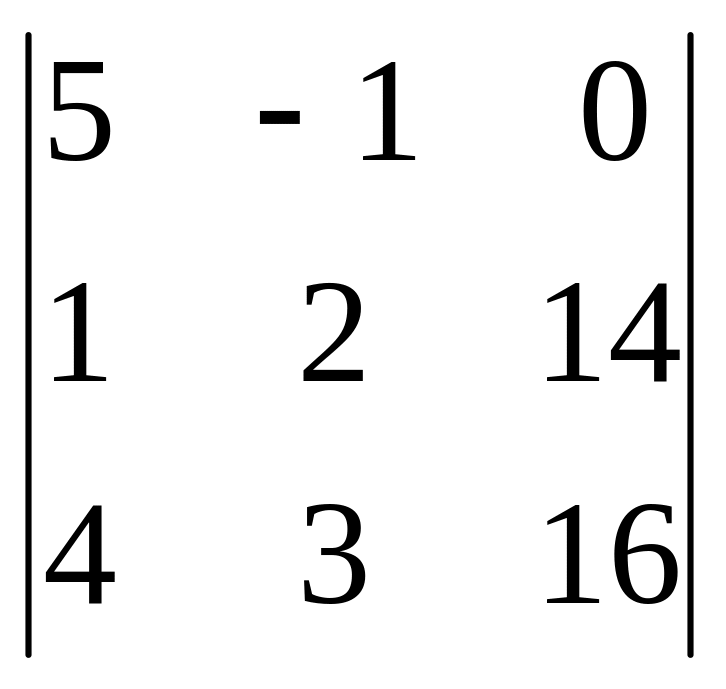 = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
x3 = 3/ = 3.
Як бачимо, результат збігається з результатом, отриманим вище матричним методом.
Якщо система однорідна, тобто bi = 0, то при 0 система має єдине нульове рішення: x1 = x2 = … = xn = 0.
При = 0 система має безкінечну множину рішень.
Для самостійного рішення:
![]() ;
Відповідь:
x
= 0; y
= 0; z
= -2.
;
Відповідь:
x
= 0; y
= 0; z
= -2.
Розв’язання довільних систем лінійних рівнянь.
Як було сказано вище, матричний метод і метод Крамера застосовні тільки до тих системам лінійних рівнянь, в яких число невідомих дорівнює числу рівнянь. Далі розглянемо довільні системи лінійних рівнянь. Визначення. Система m рівнянь з n невідомими в загальному вигляді записується наступним чином:
![]() ,
,
де aij – коефіцієнти, а bi – постійні. Рішеннями системи є n чисел, які при підстановці в систему перетворюють кожне її рівняння в тотожність. Визначення. Якщо система має хоча б одне рішення, то вона називається сумісною. Якщо система не має жодного рішення, то вона називається несумісною. Визначення. Система називається визначеною, якщо вона має тільки одне рішення і невизначеною, якщо більше одного.
Визначення. Для системи лінійних рівнянь матриця
А = називається матрицею системи, а матриця
А*=
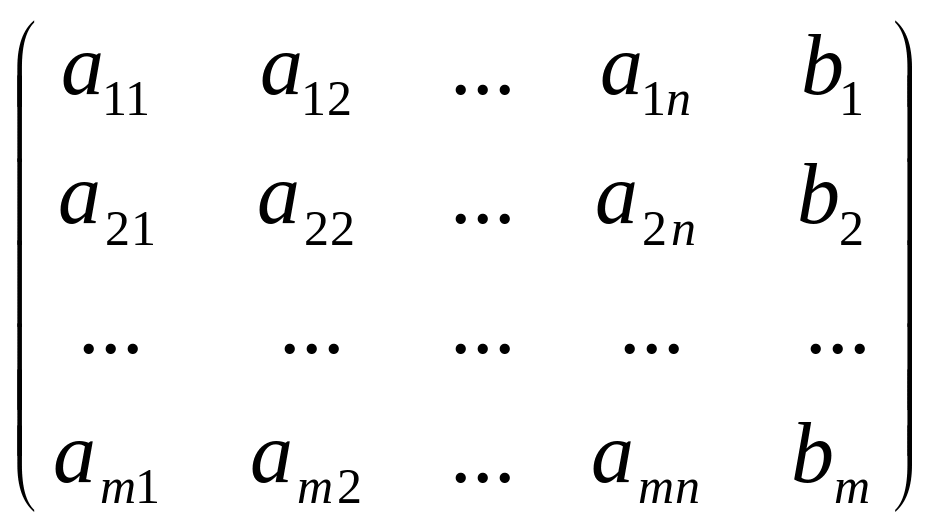 називається розширеною матрицею системи
називається розширеною матрицею системи
Визначення. Якщо b1, b2, …,bm = 0, то система називається однорідною. Однорідна система завжди сумісна, так як завжди має нульове рішення.
Елементарні перетворення систем.
До елементарних перетворень відносяться:
1) Додаток до обох частин одного рівняння відповідних частин іншого, помножених на одне і те ж число, не рівне нулю.
2) Перестановка рівнянь місцями.
3) Вилучення з системи рівнянь, які є тотожністю для всіх х.
Теорема Кронекера - Капеллі. (умова спільності системи) (Леопольд Кронекер (1823-1891) німецький математик)
Теорема. Система сумісна (має хоча б одне рішення) тоді і тільки тоді, коли ранг матриці системи дорівнює рангу розширеної матриці.
RgA = RgA *.
Очевидно, що система може бути записана у вигляді:
x1![]() + x2
+ x2
![]() +
… + xn
+
… + xn
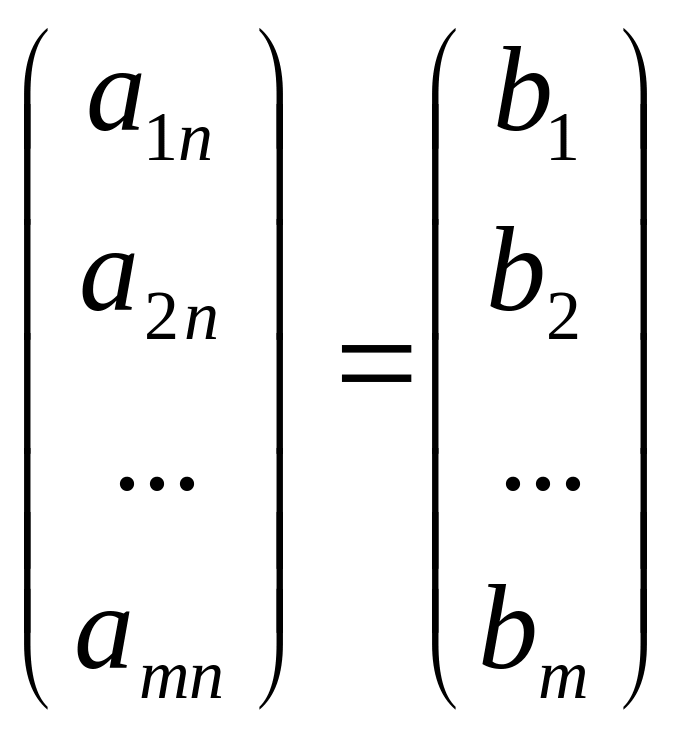
Доведення. 1) Якщо рішення існує, то стовпець вільних членів є лінійна комбінація стовпців матриці А, а значить додавання цього стовпця в матрицю, тобто перехід А А * не змінюють рангу. 2) Якщо RgA = RgA *, то це означає, що вони мають один і той же базисний мінор. Стовпець вільних членів - лінійна комбінація стовпців базисного мінору, то вірний запис, наведений вище. Приклад. Визначити спільність системи лінійних рівнянь:
![]()
A
=
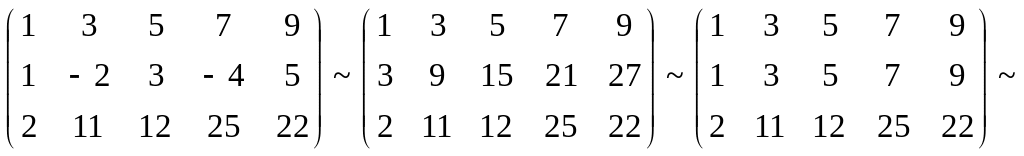
~
![]() .
.
![]() RgA
= 2.
RgA
= 2.
A*
=
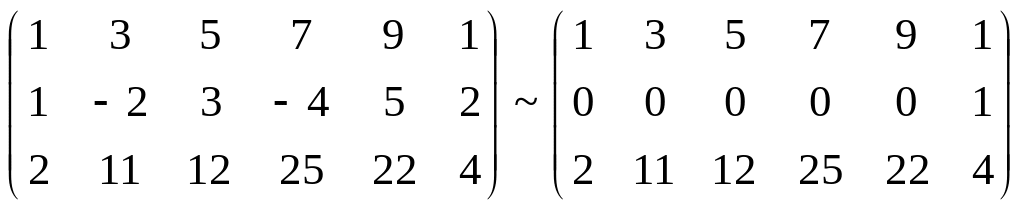 RgA*
= 3.
RgA*
= 3.
Система несумісна.
Приклад. Визначити спільність системи лінійних рівнянь:
![]() А =
А =
 ;
;
![]() = 2 + 12 = 14
0; RgA
= 2;
= 2 + 12 = 14
0; RgA
= 2;
A*
=
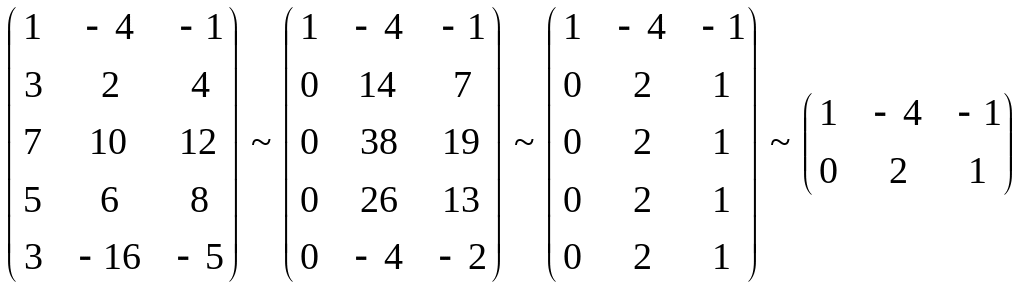
![]() RgA*
= 2.
RgA*
= 2.
Система сумісна. Відповідь: x1 = 1; x2 =1/2.
Метод Гаусса. (Карл Фрідріх Гаусс (1777-1855) німецький математик)
На відміну від матричного методу і методу Крамера, метод Гаусса може бути застосований до систем лінійних рівнянь з довільним числом рівнянь та невідомих. Суть методу полягає в послідовному виключенні невідомих.
Розглянемо систему лінійних рівнянь:
Розділимо обидві частини 1–го рівняння на a11 0, потім:
1) помножимо на а21 і віднімемо з другого рівняння
2) помножимо на а31 і віднімемо з третього рівняння
і т.д.
