Лінійна алгебра.

Основні визначення.

Визначення. Матрицею розміру mn, де m- число рядків, n- число стовпців, називається таблиця чисел, розташованих в певному порядку. Ці числа називаються елементами матриці. Місце кожного елемента однозначно визначається номером рядка і стовпця, на перетині яких він знаходиться. Елементи матриці позначаються a_ij, де i- номер рядка, а j- номер стовпця.

А =

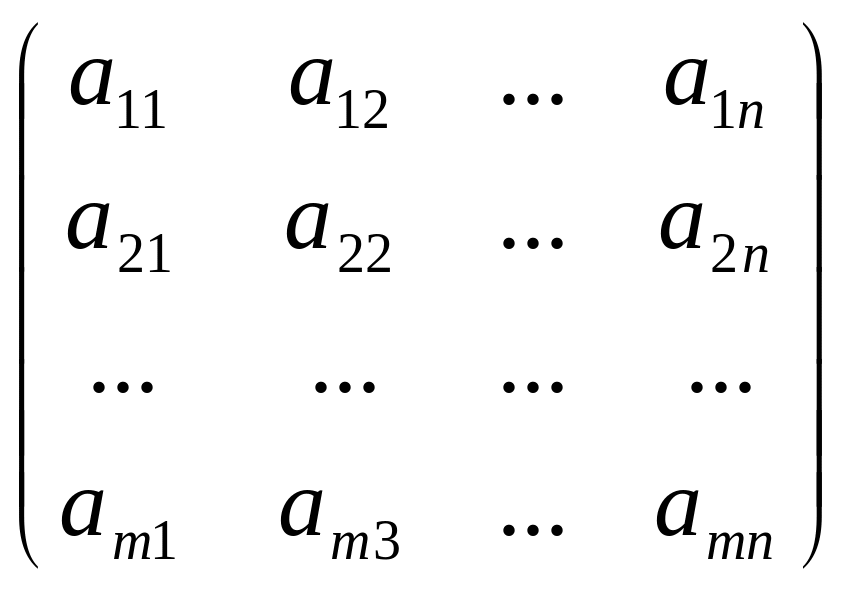
Основні дії над матрицями.

Матриця може складатися як з одного рядка, так і з одного стовпця. Взагалі кажучи, матриця може складатися навіть з одного елемента.

Визначення. Якщо число стовпців матриці дорівнює числу рядків (m=n), то матриця називається квадратною.

Визначення. Матриця виду:

= E,

називається одиничною матрицею.

Визначення. Якщо a_mn = a_nm , то матриця називається симетричною.

Приклад. 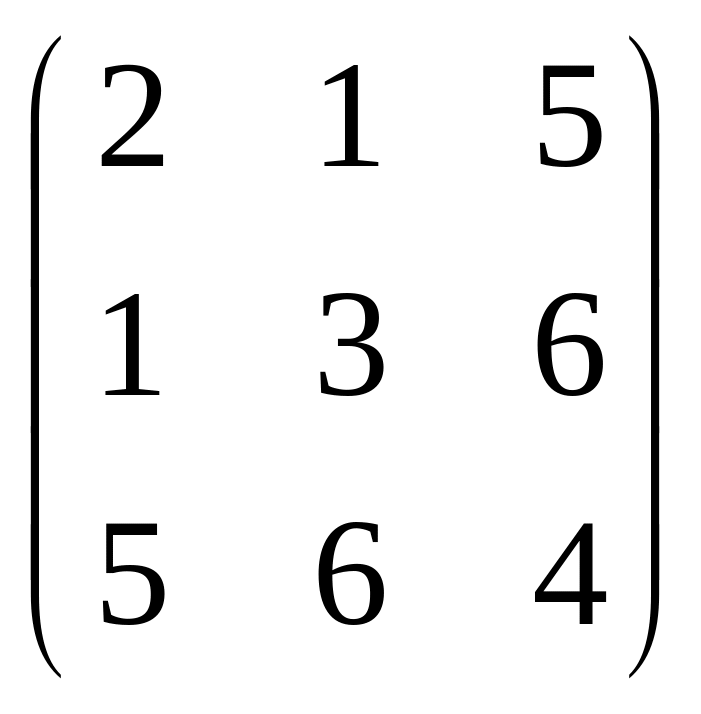- симетрична матриця

Визначення. Квадратна матриця виду 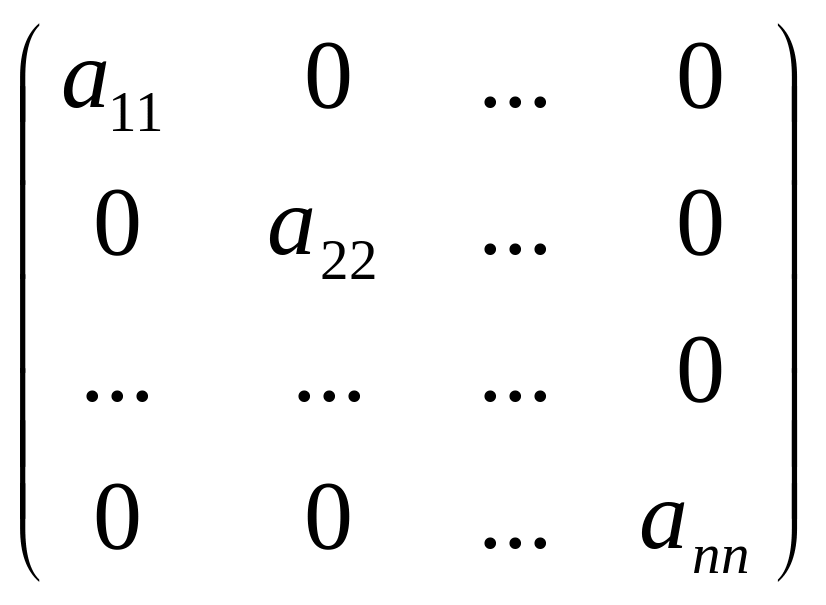називається діагональною матрицею.

Додавання і віднімання матриць зводиться до відповідних операцій над їх елементами. Найголовнішим властивістю цих операцій є те, що вони визначені тільки для матриць однакового розміру. Таким чином, можливо визначити операції додавання і віднімання матриць: Визначення. Сумою (різницею) матриць є матриця, елементами якої є відповідно сума (різниця) елементів вихідних матриць.

cij = aij  bij

С = А + В = В + А.

Операція множення (ділення) матриці будь-якого розміру на довільне число зводиться до множення (ділення) кожного елемента матриці на це число.

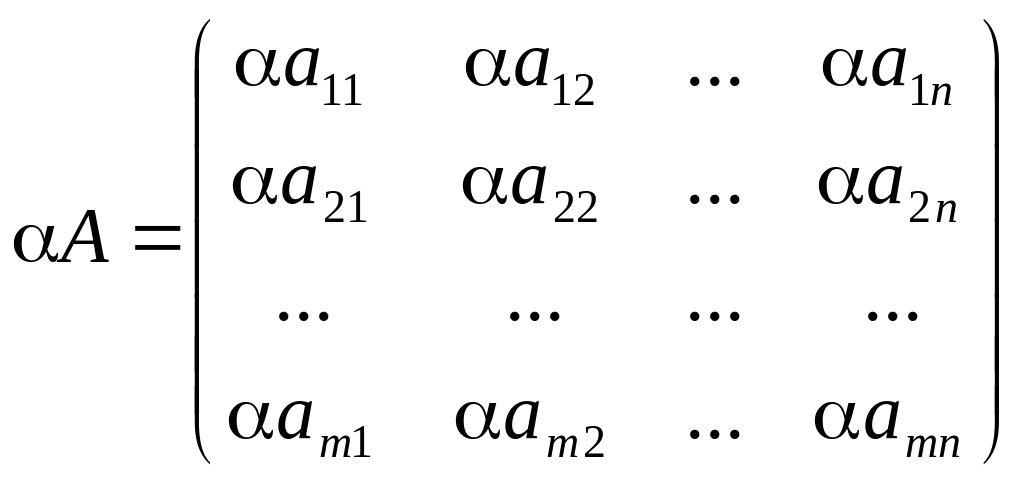
 (А+В) =А  В

А() = А  А

Приклад. Дано матриці: А = 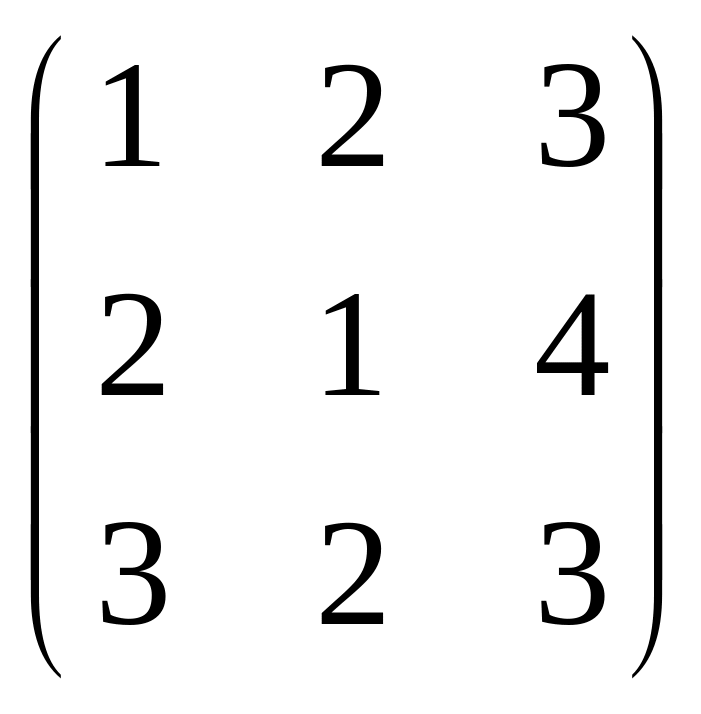; B = 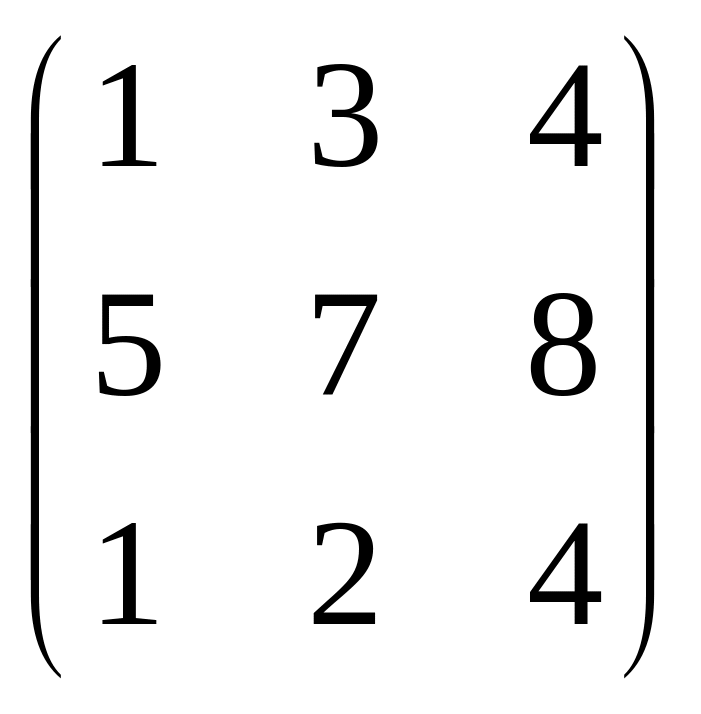, знайти 2А + В.

2А = , 2А + В = .

Операції множення матриць.

Визначення: Добутком матриць називається матриця, елементи якої можуть бути обчислені за наступними формулами:

AB = C;

З наведеного визначення видно, що операція множення матриць визначена тільки для матриць, число стовпців першої з яких дорівнює числу рядків другої.

Властивості операцій множення матриць.

1. Множення матриць не є комутативне, тобто АВ  ВА навіть якщо визначені обидва добутки. Однак, якщо для будь - яких матриць співвідношення АВ = ВА виконується, то такі матриці називаються перестановочні.

Найхарактернішим прикладом може служити одинична матриця, котра є і перестановочною з будь-якою іншою матрицею того ж розміру.

Перестановочними можуть бути тільки квадратні матриці одного і того ж порядку.

АЕ = ЕА = А

Очевидно, що для будь-яких матриць виконуються наступне властивість:

AO = O; OA = O,

де O- нульова матриця.

2. Операція множення матриць асоціативна, тобто якщо визначені добутки АВ і (АВ) С, то визначені ВС і А(ВС), і виконується рівність:

(АВ)С=А(ВС).

3. Операція множення матриць дистрибутивна по відношенню до додавання, тобто якщо мають сенс висловлювання А(В + С) та (А + В)С, то відповідно: А(В + С) = АВ + АС

(А + В)С = АС + ВС.

4) Якщо добуток АВ визначено, то для будь-якого числа  вірно співвідношення:  (AB) = ( A) B = A ( B).

5) Якщо визначено добуток АВ, то і визначено добуток В^ТА^Т і виконується рівність: (АВ)^Т = В^ТА^Т,

де індексом Т позначається транспонована матриця. 6) Зауважимо також, що для будь-яких квадратних матриць det (AB) = detBdetA. Поняття det (визначник, детермінант) буде розглянуто нижче.

Визначення. Матрицю В називають транспонованою матрицею А, а перехід від А до В транспонування, якщо елементи кожного рядка матриці А записати в тому ж порядку в стовпці матриці В.

А = 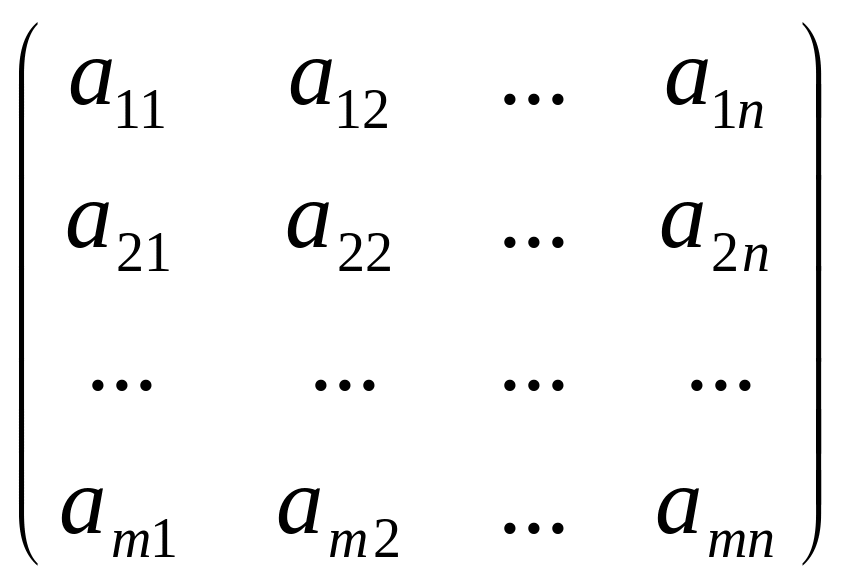; В = А^Т= ;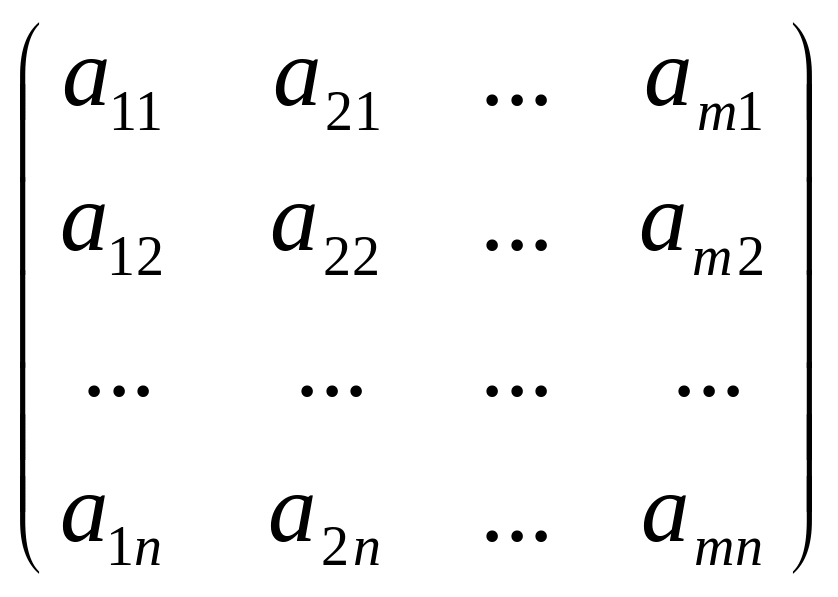

іншими словами, b_ji = a_ij.

В якості слідства з попереднього властивості (5) можна записати, що: (ABC)^T = C^TB^TA^T, за умови, що визначено добуток матриць АВС. Приклад. Дано матриці А = 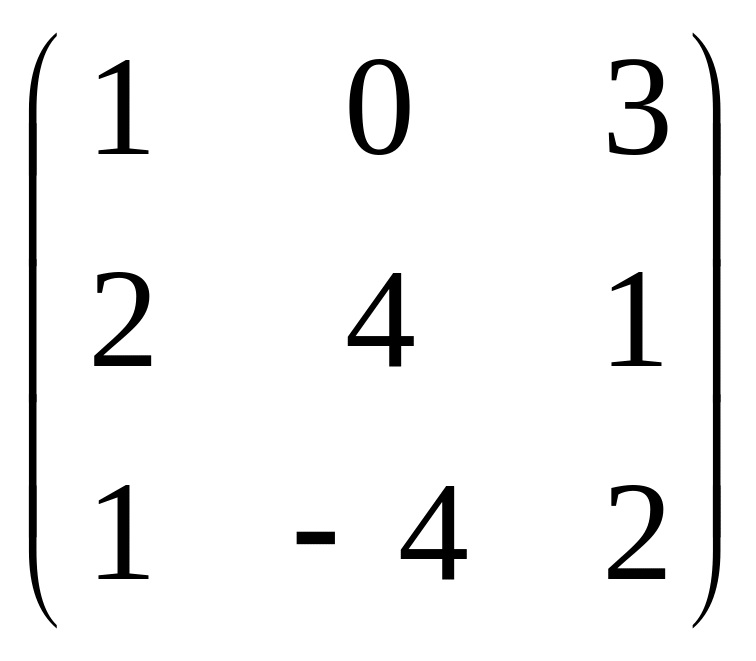, В = , С = і число  = 2.

Знайти А^ТВ+С.

A^T = 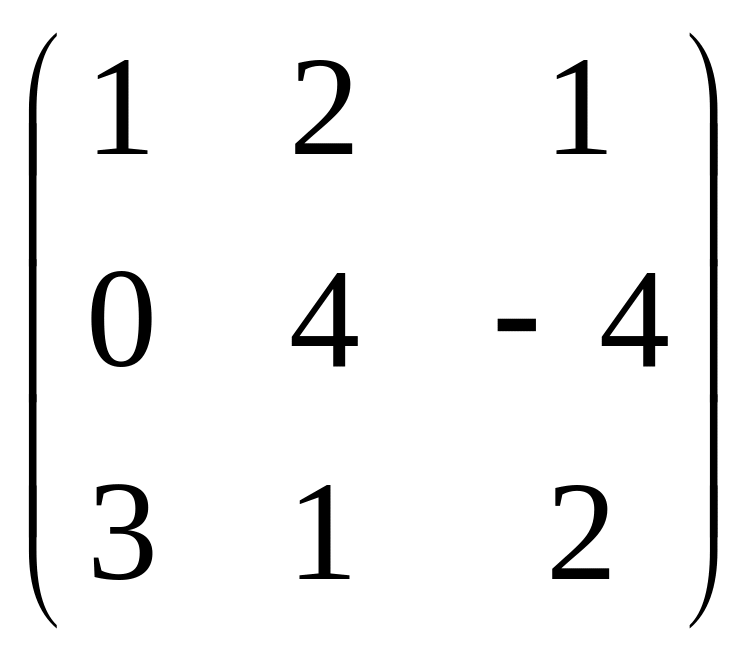; A^TB =  = = ;

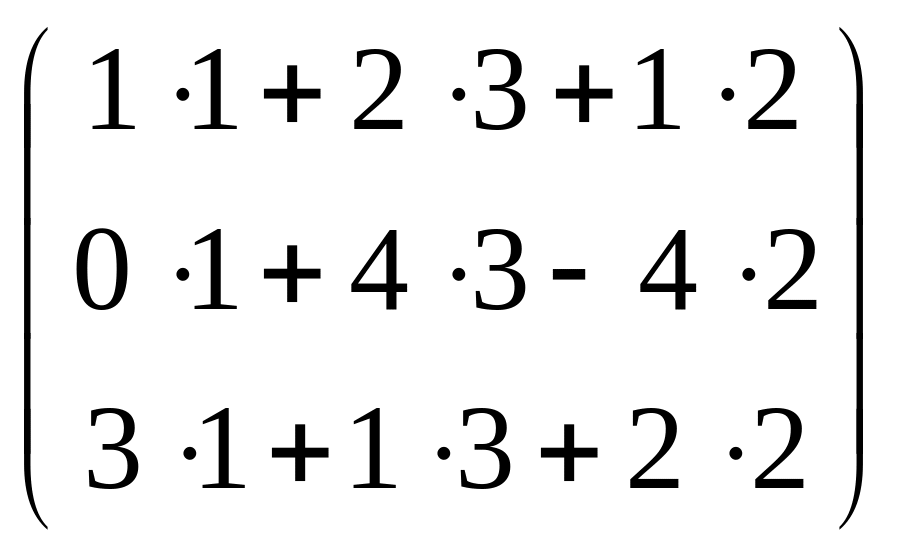C = ; А^ТВ+С = + = .

Приклад. Знайти добуток матриць А = і В = . АВ =  = .

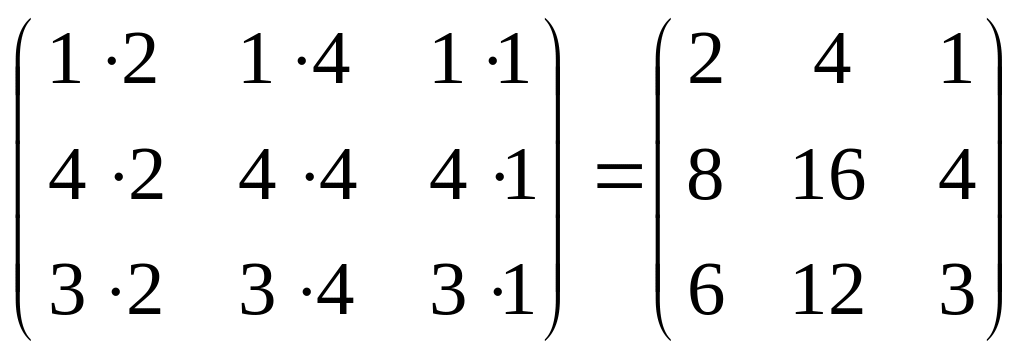ВА =  = 21 + 44 + 13 = 2 + 16 + 3 = 21.

Приклад. Знайти добуток матриць А= , В =

АВ =  = = .

Визначники(Детермінанти).

det A = ,

 Визначення. Визначником квадратної матриці А= 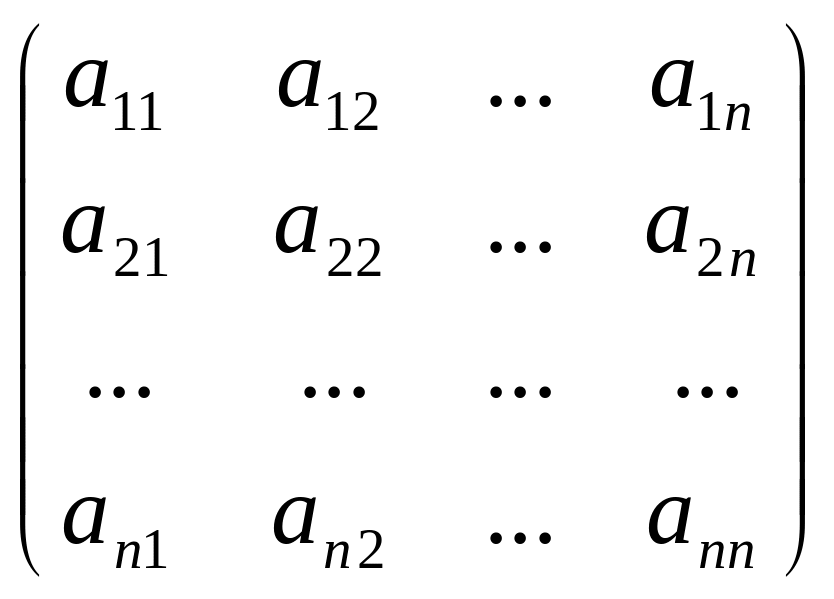називається число, яке може бути обчислено за елементами матриці за формулою:

                                                        

  де

det A =

М_1к - детермінант матриці, отриманої з вихідної викреслюванням першого рядка і k - го стовпця. Слід звернути увагу на те, що визначники мають тільки квадратні матриці, тобто матриці, у яких число рядків дорівнює числу стовпців.

Попередня формула дозволяє обчислити визначник матриці по першому рядку, також справедлива формула обчислення визначника по першому стовпцю:
                                                                

detA= , i = 1,2,…,n.

Взагалі кажучи, визначник може обчислюватися по будь-якому рядку або стовпцю матриці, тобто справедлива формула:

                                                     

Очевидно, що різні матриці можуть мати однакові визначники.  Визначник одиничної матриці дорівнює 1.

Для зазначеної матриці А число М_1к називається додатковим мінором елемента матриці a_1k. Таким чином, можна зробити висновок, що кожен елемент матриці має свій додатковий мінор. Додаткові мінори існують тільки в квадратних матрицях.

Визначення. Додатковий мінор довільного елемента квадратної матриці aij дорівнює визначнику матриці, отриманої з вихідної викреслюванням I-го рядка і j-го стовпця.

Властивість 1. Важливою властивістю визначників є наступне співвідношення: detA=detA^T;

Властивість 2. det(AB)=detAdetB.

Властивість 3. Якщо в квадратній матриці поміняти місцями будь два рядки (або стовпця), то визначник матриці змінить знак, не змінившись в абсолютній величині. Властивість 4. При множенні стовпця (або рядка) матриці на число її визначник помножується на це число. Визначення: Стовпці (рядки) матриці називаються лінійно залежними, якщо існує їх лінійна комбінація, рівна нулю, що має нетривіальні (не рівні нулю) рішення. Властивість 6. Якщо в матриці А рядки або стовпці лінійно залежні, то її визначник дорівнює нулю. Властивість 7. Якщо матриця містить нульовий стовпець або нульову рядок, то її визначник дорівнює нулю. (Дане твердження очевидно, тому вважати визначник можна саме за нульовою рядку або стовпцю.) Властивість 8. Визначник матриці не зміниться, якщо до елементів однієї з його рядків (стовпців) додати (відняти) елементи іншого рядка (стовпця), помножені на якесь число, не рівне нулю. Властивість 9. Якщо для елементів якої-небудь рядка або стовпця матриці вірно співвідношення: d = d₁  d₂ , e = e₁  e₂ , f = f₁  f₂ , то вірно:

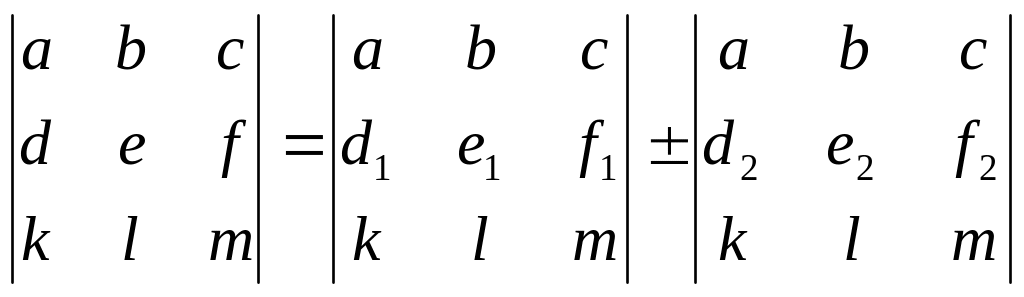
Приклад. Обчислити визначник матриці А =

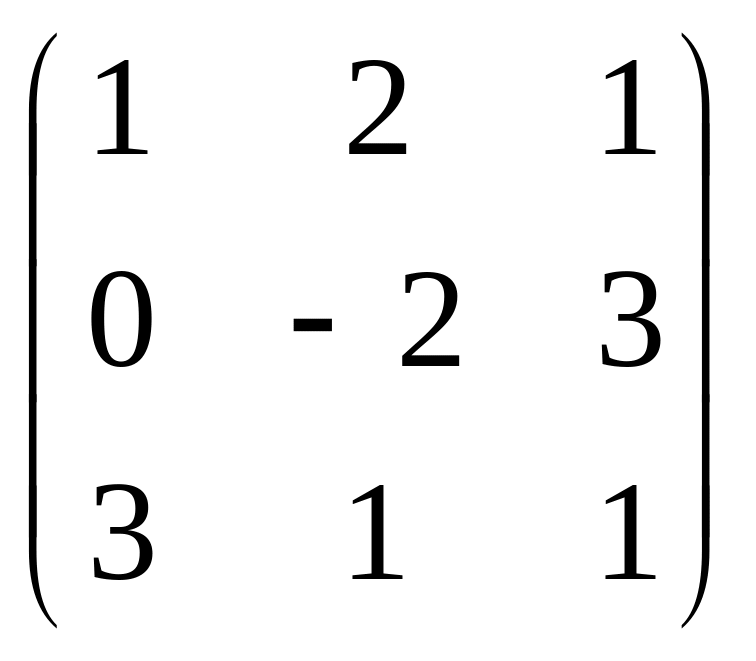
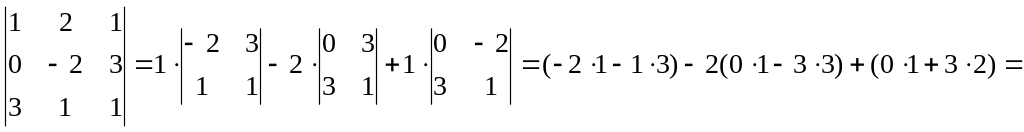
= -5 + 18 + 6 = 19.

Приклад. Дані матриці А = , В = .

Знайти det (AB).

1-ий спосіб: det A = 4 – 6 = -2; det B = 15 – 2 = 13; det (AB) = det A detB = -26.

2-ий спосіб: AB = , det (AB) = 718 - 819 = 126–

– 152 = -26.

Елементарні перетворення матриці.

Визначення. Елементарними перетвореннями матриці назвемо наступні перетворення: 1)множення рядка на число, відмінне від нуля;

2)додаток до елементів одного рядка елементів іншого рядка;

3)перестановка рядків;

4)викреслення (видалення) однієї з однакових рядки (стовпчики);

5)транспонування; Ті ж операції, що застосовуються для стовпців, також називаються елементарними перетвореннями. За допомогою елементарних перетворень можна до будь-якої рядку або стовпцю додати лінійну комбінацію інших рядків (стовпців). Мінори.

Вище було використано поняття додаткового мінору матриці. Дамо визначення мінору матриці. Визначення. Якщо в матриці А виділити кілька довільних рядків і стільки ж довільних стовпців, то визначник, складений з елементів, розташованих на перетині цих рядків і стовпців називається мінором матриці А. Якщо виділено s рядків і стовпців, то отриманий мінор називається мінором порядку s.

Зауважимо, що вищесказане застосовано не тільки до квадратних матриць, а й до прямокутних. Якщо викреслити з вихідної квадратної матриці А виділені рядки і стовпці, то визначник отриманої матриці буде додатковим мінором.