
Лабораторна робота № 4. Елементарні методи розв’язання ігор
Мета роботи. Ознайомитися з методами розв’язання невеликих за розмірами задач теорії ігор
Основний теоретичний матеріал
Якщо гра т х п не має сідлової точки, то знаходження розв’язання є взагалі досить важке завдання, особливо при великих т и п.
Іноді це завдання вдається спростити, якщо попередньо зменшити число стратегій шляхом викреслювання деяких зайвих. Зайві стратегії бувають: а) дублюючі; б) свідомо невигідні. Розглянемо наприклад гру з матрицею (рис.4.1):
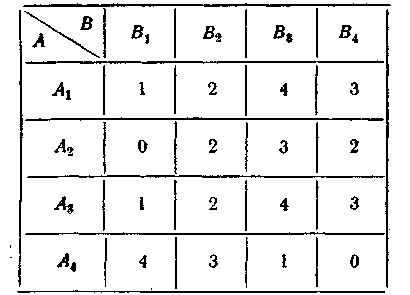
Рис. 4.1.
Неважко переконатися, що
стратегія
![]() у точності повторює
(«дублює») стратегію
у точності повторює
(«дублює») стратегію
![]() тому будь-яку із цих
двох стратегій можна викреслити.
тому будь-яку із цих
двох стратегій можна викреслити.
Д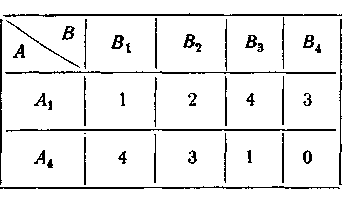 алі,
порівнюючи членами рядки
і
алі,
порівнюючи членами рядки
і
![]() ,
бачимо, що кожний елемент
рядка
,
менше (або дорівнює) відповідного
елемента рядка
.
Очевидно, що ми ніколи
не повинні користуватися стратегією
А2;
вона є
свідомо невигідною.
Викреслюючи А3
і А2,
,
бачимо, що кожний елемент
рядка
,
менше (або дорівнює) відповідного
елемента рядка
.
Очевидно, що ми ніколи
не повинні користуватися стратегією
А2;
вона є
свідомо невигідною.
Викреслюючи А3
і А2,
Рис.4.2.
приводимо матрицю до більше простого виду (рис. 4.2.). Далі зауважуємо, що для супротивника стратегія В3 свідомо невигідна; викреслюючи її, приводимо матрицю до остаточного виду (рис. 4.3). Таким чином, гра 4 х 4 викреслюванням дублюючих і свідомо невигідних стратегій зведена до гри 2 х 3.
Р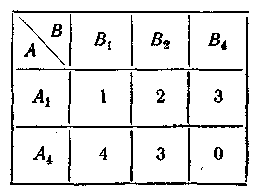 ис.
4.3.
ис.
4.3.
Процедура викреслювання дублюючих і свідомо невигідних стратегій завжди повинна передувати розв’язанню гри.
Найбільш простими випадками кінцевих ігор, які завжди можна вирішити елементарними способами, є ігри 2 х 2 і 2 х m.
Розглянемо гру 2 х 2 з матрицею:
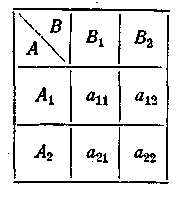
Рис.4.4.
Тут можуть зустрітися два випадки: 1) гра має сідлову точку; 2) гра не має сідлової точки. У першому випадку розв’язання очевидно: це пари стратегій, що перетинаються в сідловій точці. Помітимо до речі, що в грі 2 х 2 наявність сідлової точки завжди відповідає існуванню свідомо невигідних стратегій, які повинні бути викреслені при попередньому аналізі.
Нехай сідлової точки немає
й, отже, нижня ціна гри
не дорівнює верхній:
![]() .
Потрібно знайти оптимальну змішану
стратегію гравця А:
.
Потрібно знайти оптимальну змішану
стратегію гравця А:
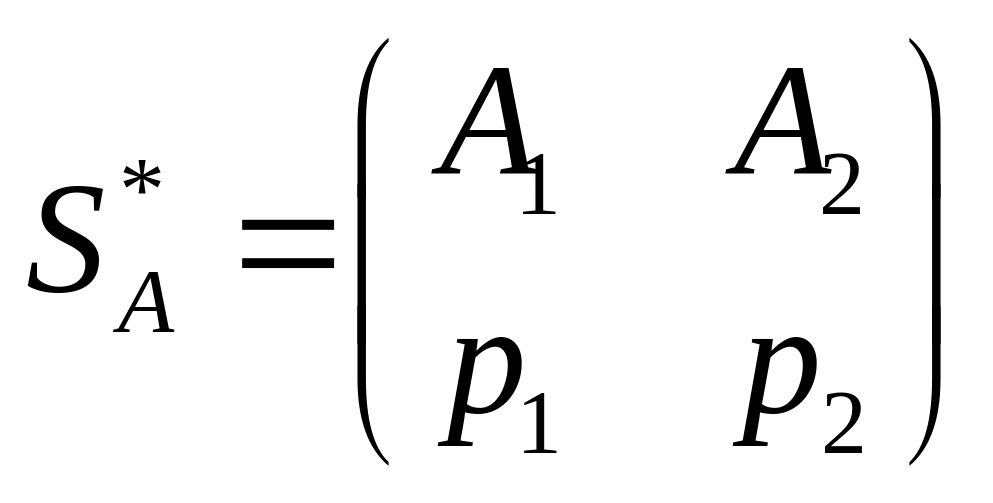
Вона відрізняється такою
властивістю: які б не були дії супротивника
(якщо тільки він не виходить за межі
своїх «корисних» стратегій), виграш
буде дорівнювати ціні гри
![]() .
У грі 2х2 обидві стратегії супротивника
є «корисними», - інакше гра мала б
розв’язання в області чистих стратегій
(сідлову точку). Виходить, якщо ми
дотримуємося своєї оптимальної стратегії
,
то супротивник може користуватися
будь-якою з своїх чистих стратегій
.
У грі 2х2 обидві стратегії супротивника
є «корисними», - інакше гра мала б
розв’язання в області чистих стратегій
(сідлову точку). Виходить, якщо ми
дотримуємося своєї оптимальної стратегії
,
то супротивник може користуватися
будь-якою з своїх чистих стратегій
![]() ,
не змінюючи середнього
виграшу
.
Звідси маємо два рівняння:
,
не змінюючи середнього
виграшу
.
Звідси маємо два рівняння:
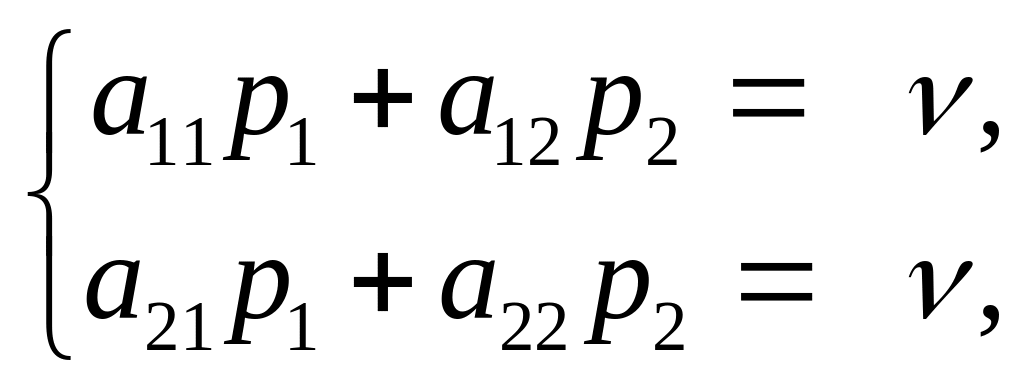 (4.1)
(4.1)
з яких, беручи до уваги, що
![]() ,
одержимо:
,
одержимо:
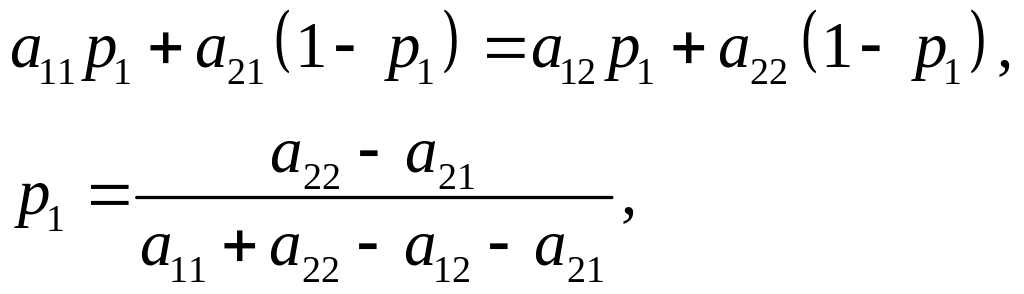 (4.2)
(4.2)
Ціну гри ν
знайдемо, підставляючи значення
![]() у будь-яке з рівнянь (4.1).
у будь-яке з рівнянь (4.1).
Якщо ціна гри відома, то для.
визначення оптимальної стратегії
супротивника
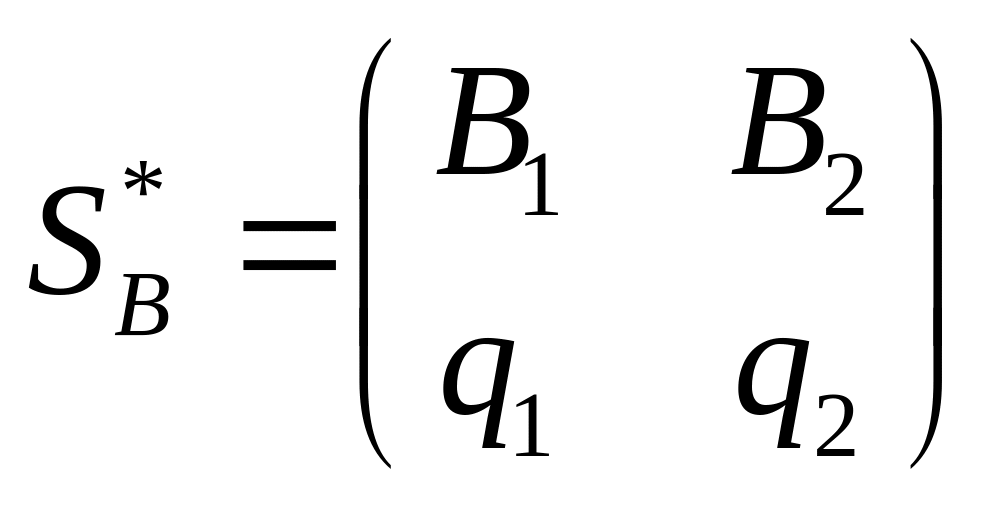 досить одного рівняння, наприклад:
досить одного рівняння, наприклад:
![]() ,
,
звідки, з огляду на, що
![]() ,
маємо:
,
маємо:
![]() .
.
Приклад 4.1. Два гравці А і В, не дивлячись один на одного, кладуть на стіл по монеті нагору гербом або нагору цифрою, за своїм розсудом. Якщо гравці вибрали однакові сторони (в обох герб або в обох цифра), то гравець А забирає обидві монети; інакше їх забирає гравець В. Потрібно проаналізувати гру й скласти її матрицю.
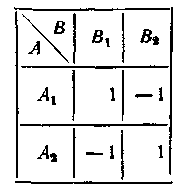
Рис. 4.5.
Гра не має сідлової точки
(![]() ),
і, отже, розв’язання повинне лежати в
області змішаних стратегій:
),
і, отже, розв’язання повинне лежати в
області змішаних стратегій:
,
Потрібно знайти
і
![]() .
.
Для
![]() маємо рівняння
маємо рівняння
![]() ,
,
звідки
![]() .
.
Аналогічно знайдемо:
![]() .
.
Отже, оптимальна стратегія для кожного з гравців полягає в тому, щоб випадковим образом чергувати обидві свої чисті стратегії, користуючись однаково часто кожною з них; при цьому середній виграш буде дорівнює нулю.
Отриманий висновок був досить ясний заздалегідь. У наступному прикладі ми розглянемо більше складну гру, розв’язання якої не є настільки очевидним. Приклад являє собою елементарний зразок ігор, відомих за назвою ігор з «обманом» або «введенням в оману». На практиці в конфліктних ситуаціях часто застосовуються різні способи введення супротивника в оману (дезінформація, розміщення помилкових цілей і т.д.). Приклад, незважаючи на свою простоту, досить повчальний.
Приклад 4.2. Гра полягає в наступному. Є дві карти: туз і двійка. Гравець А навмання виймає одну з них; В не бачить, яку карту він вийняв. Якщо А вийняв туза, він заявляє: «у мене туз», і вимагає в супротивника 1 гривню. Якщо А вийняв двійку, то він може або ) сказати «у мене туз» і зажадати в супротивника 1 гривню, або ) зізнатися, що в нього двійка, і сплатити супротивникові 1 гривню.
Супротивник, якщо йому
добровільно платять 1 гривню, може тільки
прийняти її. Якщо ж у нього зажадають 1
гривню, то він може або
![]() )
повірити гравцеві А, що
в нього туз, і віддати йому 1 гривню, або
В2)
зажадати перевірки для
того, щоб переконатися, чи вірно твердження
А. Якщо
в результаті перевірки виявиться, що в
А дійсно
туз, В повинен
сплатити А 2
гривні. Якщо ж виявиться, що А
обманює й у нього двійка,
гравець А сплачує
гравцеві В 2
гривні.
)
повірити гравцеві А, що
в нього туз, і віддати йому 1 гривню, або
В2)
зажадати перевірки для
того, щоб переконатися, чи вірно твердження
А. Якщо
в результаті перевірки виявиться, що в
А дійсно
туз, В повинен
сплатити А 2
гривні. Якщо ж виявиться, що А
обманює й у нього двійка,
гравець А сплачує
гравцеві В 2
гривні.
Потрібно проаналізувати гру й знайти оптимальну стратегію кожного із гравців.
Розв’язання. Гра має порівняно складну структуру; вона складається з одного обов'язкового випадкового ходу — вибору гравцем А однієї із двох карт — і двох особистих ходів, які, однак, необов'язково здійснюються. Дійсно, якщо А вийняв туза, то він не робить ніякого особистого ходу: йому надана тільки одна можливість — зажадати 1 гривню, що він і робить. У цьому випадку особистий хід — вірити або не вірити (тобто платити або не платити 1 гривню,) — передається гравцеві В. Якщо А в результаті першого випадкового ходу одержав двійку, то йому надається особистий хід: сплатити 1 гривню або спробувати обдурити супротивника й зажадати 1 гривню (коротше: «не обманювати» або «обманювати»). Якщо А вибирає перше, то В залишається тільки прийняти 1 гривню; якщо А вибрав друге, то гравцеві В надається особистий хід: вірити чи не вірити А (тобто сплатити А 1 гривню або вимагати перевірки).
Стратегії кожного із гравців являють собою правила, що вказують, як діяти гравцеві, коли йому надається особистий хід.
Очевидно, в А тільки дві стратегії:
А1 — обманювати, А2 — не обманювати.
У В— теж дві стратегії:
Β1·—вірити, В2 — не вірити.
Побудуємо матрицю гри. Для цього обчислимо середній виграш при кожній комбінації стратегій.
1. A1B1 (А обманює, В вірить).
Якщо А одержав туза (імовірність цього -1/2), то йому не надається особистого ходу; він вимагає 1 гривню, і гравець В вірить йому; виграш А в гривнях дорівнює 1.
Якщо А одержав двійку (імовірність цього теж –1/2), він відповідно до своєї стратегії обманює й вимагає 1 гривню; В йому вірить і сплачує; виграш А також дорівнює 1. Середній виграш:
![]()
2. ![]() (А обманює, В
не вірить).
(А обманює, В
не вірить).
Якщо А одержав туза, у нього немає особистого ходу; він вимагає 1 гривню; В згідно своїй стратегії не вірить і в результаті перевірки сплачує 2 гривні (виграш А дорівнює - +2).
Якщо А одержав двійку, він відповідно до своєї стратегії вимагає 1 гривню; В, відповідно до своєї, не вірить; у результаті А сплачує 2 гривні (виграш А дорівнює -2). Середній виграш дорівнює:
![]()
3. ![]() (А не обманює, В
вірить).
(А не обманює, В
вірить).
Якщо А вийняв туза, він вимагає 1 гривню; В згідно своїй стратегії сплачує; виграш А дорівнює +1. Якщо А вийняв двійку, він відповідно до своєї стратегії платить 1 гривню; В залишається тільки прийняти (виграш А дорівнює -1). Середній виграш дорівнює:
![]()
4.
![]() (А не обманює, У
не вірить).
(А не обманює, У
не вірить).
Якщо А вийняв туза, він вимагає 1 гривню; В перевіряє й у результаті перевірки сплачує 2 гривні (виграш дорівнює +2).
Якщо А вийняв двійку, він сплачує 1 гривню; В залишається тільки прийняти (виграш дорівнює -1).
Середній виграш дорівнює:
![]() .
.
Будуємо матрицю гри (рис.4.6).
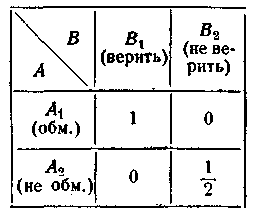
Рис.4.6.
Матриця
не має сідлової точки. Нижня
ціна гри
![]() ,
верхня ціна гри
,
верхня ціна гри
![]() .
Знайдемо розв’язання гри в області
змішаних стратегій. Застосовуючи формулу
(4.2), одержимо:
.
Знайдемо розв’язання гри в області
змішаних стратегій. Застосовуючи формулу
(4.2), одержимо:
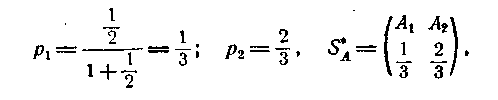
тобто гравець А
повинен в одній третині
всіх випадків користуватися своєю
першою стратегією (обманювати), а у двох
третинах — другої (не обманювати). При
цьому він буде вигравати в середньому
ціну гри
![]() .
.
Значення свідчить про те, що в даних умовах гра вигідна для А и невигідна для В. Користуючись своєю оптимальною стратегією, А завжди може собі забезпечити позитивний середній виграш.
Помітимо, що, якби А користувався своєї найбільш обережною (максимінною) стратегією (у цьому випадку обидві стратегії й є максимінними), він мав би середній виграш, що дорівнює нулю. Таким чином, застосування змішаної стратегії дає А можливість реалізувати своя перевагу над В, що виникає при даних правилах гри.
Визначимо оптимальну стратегію В. Маємо:
![]()
звідки
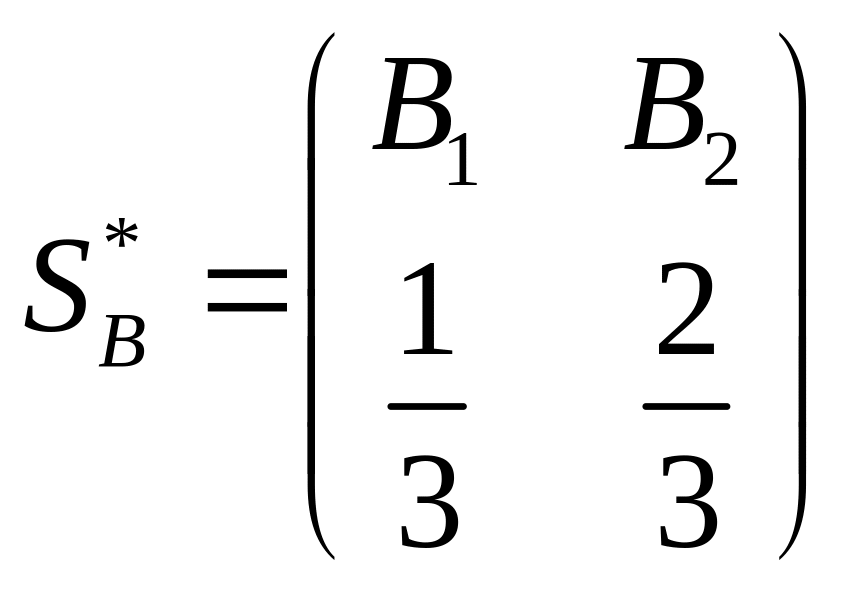 ,
тобто гравець В
повинен в одній третій всіх випадків
вірити А
і виплачувати йому 1 гривню без перевірки,
а в двох третіх випадків – перевіряти.
Тоді він буде в середньому на кожну гру
програвати
,
тобто гравець В
повинен в одній третій всіх випадків
вірити А
і виплачувати йому 1 гривню без перевірки,
а в двох третіх випадків – перевіряти.
Тоді він буде в середньому на кожну гру
програвати
![]() .
Якби він користувався своєю мінімаксною
чистою стратегією
.
Якби він користувався своєю мінімаксною
чистою стратегією
![]() (не вірити), він кожну гру програвав би
в середньому
(не вірити), він кожну гру програвав би
в середньому
![]() .
.
Розв’язанню гри 2 х 2 можна дати просту геометричну інтерпретацію. Нехай маємо гру 2 х 2 з матрицею, яка наведена на рис. 4.7.
|
|
|
|
|
|
|
|
|
Рис. 4.7.
Візьмемо проміжок осі абсцис
одиничної довжини (рис.4.8). Лівий кінець
проміжку (точка
![]() )
відображатиме стратегію
;
правий кінець проміжку (
)
відображатиме стратегію
;
правий кінець проміжку (![]() )
- стратегію
.
Проведемо через точки
і
два перпендикуляри до осі абсцис: вісь
)
- стратегію
.
Проведемо через точки
і
два перпендикуляри до осі абсцис: вісь
![]() і вісь
і вісь
![]() .
На осі
будемо відкладати виграші при стратегії
;
на осі
будемо відкладати виграші при стратегії
.
Розглянемо стратегію супротивника
;
вона дає дві точки на осях
і
з ординатами відповідно
і
.
Проведемо через ці точки пряму
.
На осі
будемо відкладати виграші при стратегії
;
на осі
будемо відкладати виграші при стратегії
.
Розглянемо стратегію супротивника
;
вона дає дві точки на осях
і
з ординатами відповідно
і
.
Проведемо через ці точки пряму
![]() .
Якщо ми при стратегії супротивника
будемо застосовувати змішану стратегію
.
Якщо ми при стратегії супротивника
будемо застосовувати змішану стратегію
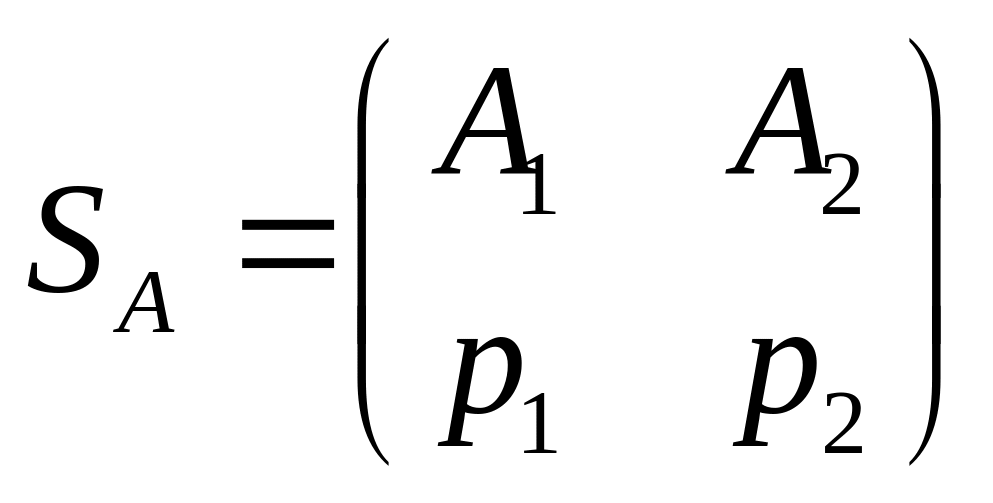 ,
то наш середній виграш, рівний у цьому
випадку
,
то наш середній виграш, рівний у цьому
випадку
![]() ,
зобразиться точкою Μ
на прямій
;
абсциса цієї точки
дорівнює
,
зобразиться точкою Μ
на прямій
;
абсциса цієї точки
дорівнює
![]() .
Пряму
,
яка відображає виграш при стратегії
,
будемо умовно називати «стратегією
».
.
Пряму
,
яка відображає виграш при стратегії
,
будемо умовно називати «стратегією
».
Очевидно, точно таким же способом може бути побудована й стратегія В2 (рис. 4.8).
Нам потрібно знайти оптимальну
стратегію
![]() ,
тобто таку, для якої
мінімальний виграш (при будь-якому
поводженні В) обертався
б у максимум. Для цього побудуємо
,
тобто таку, для якої
мінімальний виграш (при будь-якому
поводженні В) обертався
б у максимум. Для цього побудуємо
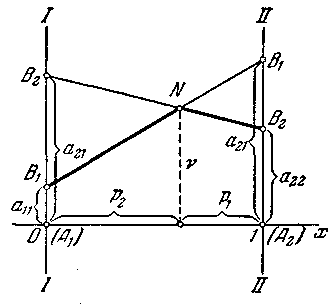
Рис. 4.8.
нижню границю виграшу при
стратегіях
![]() ,
тобто ламану
,
тобто ламану
![]() ,
відзначену на рис 4.8
жирною лінією. Ця нижня границя буде
виражати мінімальний виграш гравця А
при будь-яких його
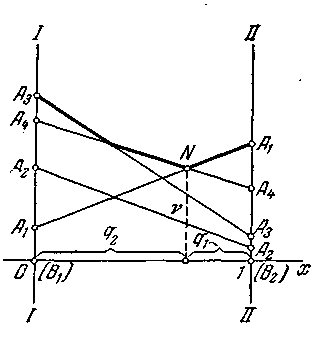
змішаних стратегіях; точка Ν,
у якій цей мінімальний
виграш досягає максимуму, і визначає
розв’язання й ціну гри. Неважко
переконатися, що ордината точки N
є ціна гри ν,
а її абсциса дорівнює
р2
—
частоті застосування стратегії А2
в
оптимальній змішаній
стратегії
.
,
відзначену на рис 4.8
жирною лінією. Ця нижня границя буде
виражати мінімальний виграш гравця А
при будь-яких його
змішаних стратегіях; точка Ν,
у якій цей мінімальний
виграш досягає максимуму, і визначає
розв’язання й ціну гри. Неважко
переконатися, що ордината точки N
є ціна гри ν,
а її абсциса дорівнює
р2
—
частоті застосування стратегії А2
в
оптимальній змішаній
стратегії
.
У нашім випадку розв’язання
гри визначалося точкою перетину
стратегій. Однак це не завжди буде так;
на мал. 4.9 показаний випадок, коли,
незважаючи на наявність перетину
стратегій, розв’язання дає для обох
гравців чисті стратегії (А2
і В2),
а ціна гри
![]() .
.
У цьому випадку матриця має сідлову точку, і стратегія є свідомо невигідною, тому що при будь-якій чистій стратегії супротивника вона дає менший виграш, чим .
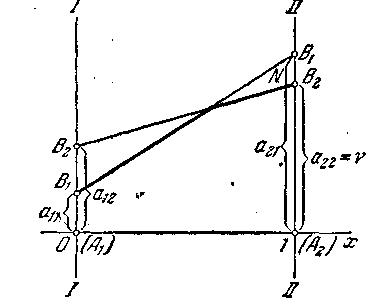
Рис. 4.9.
У випадку, коли свідомо невигідна стратегія є в супротивника, геометрична інтерпретація має вигляд, представлений на мал. 4.10.
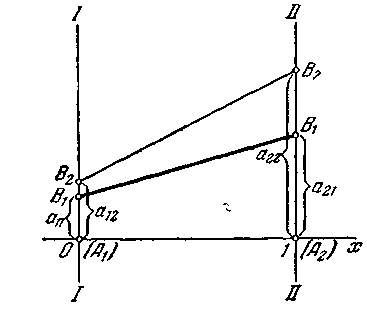
Рис. 4.10.
У цьому випадку нижня границя виграшу збігається зі стратегією , стратегія В2 для супротивника є свідомо невигідною.
Геометрична інтерпретація дає можливість представити наочно також нижню й верхню ціни гри (рис. 4.11). Для ілюстрації побудуємо геометричні
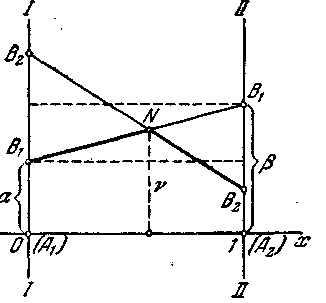
Рис. 4.11.
інтерпретації ігор 2 х 2, розглянутих у прикладах 1 і 2 (рис. 4.12 і 4.13).
Ми переконалися, що будь-яка гра 2 х 2 може бути розв’язана елементарними прийомами. Зовсім аналогічно може бути розв’язана будь-яка гра 2 х п, де в нас є всього дві стратегії, а в супротивника — довільне число.
Нехай ми використовуємо дві
стратегії:
![]() ,
а супротивник — n
стратегії:
,
а супротивник — n
стратегії:
![]() .
Матриця
.
Матриця
![]() задана; вона складається
із двох рядків і n
стовпців. Аналогічно
випадку двох стратегій дамо завданню
геометричну інтерпретацію; n
стратегій супротивника
зобразяться n прямими
(рис. 4.12).
задана; вона складається
із двох рядків і n
стовпців. Аналогічно
випадку двох стратегій дамо завданню
геометричну інтерпретацію; n
стратегій супротивника
зобразяться n прямими
(рис. 4.12).
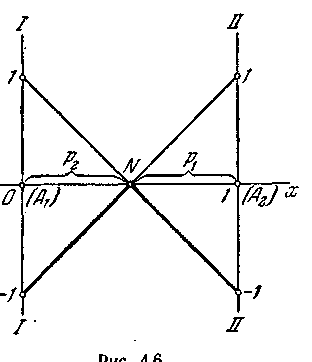
Рис. 4.12.
Будуємо нижню границю виграшу
(ламану
![]() )
і знаходимо на ній точку N
з максимальною ординатою.
Ця точка дає розв’язання гри (стратегію
);
ордината точки N дорівнює
ціні гри ν,
а абсциса дорівнює
частоті р2
стратегії
.
)
і знаходимо на ній точку N
з максимальною ординатою.
Ця точка дає розв’язання гри (стратегію
);
ордината точки N дорівнює
ціні гри ν,
а абсциса дорівнює
частоті р2
стратегії
.
У цьому випадку оптимальна
стратегія супротивника виходить
застосуванням суміші двох «корисних»
стратегій:
і
![]() ,
що перетинаються в точці N.
Стратегія В3
є свідомо невигідною,
а стратегія
- невигідною
при оптимальній стратегії
.
Якщо А буде
дотримуватися своєї оптимальної
стратегії, то виграш не зміниться, якою
би зі своїх
,
що перетинаються в точці N.
Стратегія В3
є свідомо невигідною,
а стратегія
- невигідною
при оптимальній стратегії
.
Якщо А буде
дотримуватися своєї оптимальної
стратегії, то виграш не зміниться, якою
би зі своїх
Р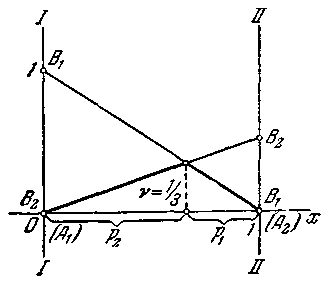 ис.4.13.
ис.4.13.
«корисних» стратегій не користувався В, однак, він зміниться, якщо В перейде до стратегій або В3. У теорії ігор доводиться, що в будь-якої кінцевої гри m x n є розв’язання, у якому число «корисних» стратегій тої й іншої сторони не перевершує найменшого
Рис. 4.14.
4.14.
із двох чисел т и п. Зокрема, із цього треба, що в гри 2 x т завжди є розв’язання; у якому з тої і іншої сторони бере участь не більше двох «корисних» стратегій.
Користуючись геометричною
інтерпретацією, можна дати простий
спосіб розв’язання будь-якої гри 2 x m.
Безпосередньо по кресленню знаходимо
пари «корисних» стратегій супротивника
![]() і
і
![]() ,
що
перетинаються в точці
N (якщо
в точці N
перетинається більше двох стратегій,
беремо будь-які дві з них). Ми знаємо, що
якщо гравець А дотримується
своєї оптимальної стратегії, то виграш
не залежить від того, у якій пропорції
застосовує В свої
«корисні» стратегії, отже,
,
що
перетинаються в точці
N (якщо
в точці N
перетинається більше двох стратегій,
беремо будь-які дві з них). Ми знаємо, що
якщо гравець А дотримується
своєї оптимальної стратегії, то виграш
не залежить від того, у якій пропорції
застосовує В свої
«корисні» стратегії, отже,
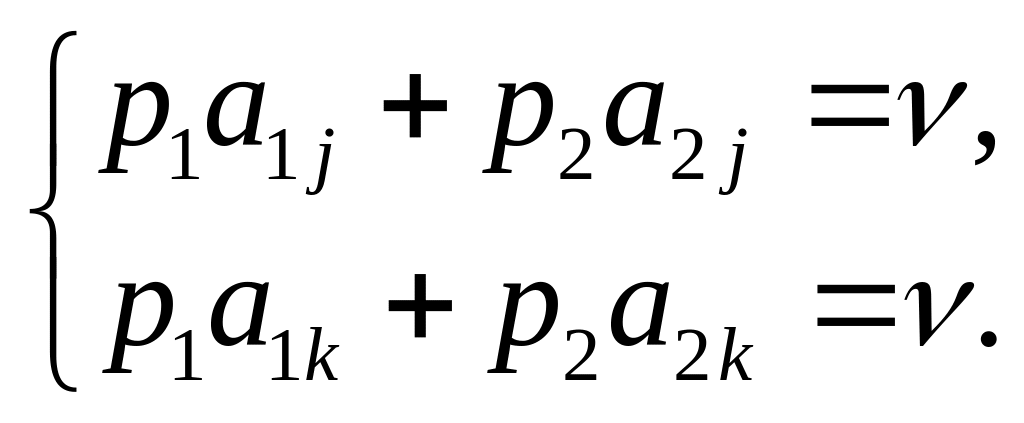
З цих
рівнянь і умови
![]() знаходимо
знаходимо
![]() і ціну гри
.
Знаючи ціну гри, можна одразу визначити
оптимальну стратегію
гравця
і ціну гри
.
Знаючи ціну гри, можна одразу визначити
оптимальну стратегію
гравця
![]() .
Для цього розв’язується, наприклад,
рівняння:
.
Для цього розв’язується, наприклад,
рівняння:
![]() ,
,
де
![]() .
.
У випадку, коли ми маємо т стратегій, а супротивник— усього дві, завдання вирішується зовсім аналогічним способом; досить помітити, що, змінюючи знак виграшу на зворотний, можна перетворити гравця А з «такого, що виграє» у «такого, що програє». Можна розв’язати гру й без зміни знака виграшу; тоді завдання вирішується безпосередньо для В, але будується не нижня, а верхня границя виграшу (рис. 4.15). На границі шукається точка N з мінімальною ординатою, що і є ціна гри v.
Розглянемо й вирішимо кілька прикладів ігор 2 х 2 і 2 х т, що є спрощеними зразками ігор, що мають практичне значення.
Приклад
4.3.
Сторона А
посилає
в район розташування супротивника
В два
бомбардувальники І
і ІІ; І
летить попереду, ІІ
— позаду. Один з бомбардувальників -
заздалегідь невідомо який — повинен
нести бомбу, іншої виконує функцію
супроводу. У районі супротивника
бомбардувальники піддаються нападу
винищувача сторони В.
Бомбардувальники
озброєні пушками різної скорострільності.
Якщо винищувач атакує задній бомбардувальник
ІІ, то
по ньому ведуть вогонь гармати тільки
цього бомбардувальника; якщо ж він
атакує передній бомбардувальник, то по
ньому ведуть вогонь гармати обох
бомбардувальників. Імовірність враження
винищувача в першому випадку p1=
0,3, у другому p2=
0,7. Якщо винищувач не збитий оборонним
вогнем бомбардувальників, то він вражає
обрану їм ціль із імовірністю
![]() =
0,6. Завдання бомбардувальників - донести
бомбу до мети; завдання винищувача -
перешкодити цьому, тобто збити
бомбардувальник-носій. Потрібно вибрати
оптимальні стратегії сторін:
=
0,6. Завдання бомбардувальників - донести
бомбу до мети; завдання винищувача -
перешкодити цьому, тобто збити
бомбардувальник-носій. Потрібно вибрати
оптимальні стратегії сторін:
а) для сторони А: який бомбардувальник зробити носієм?
б) для сторони В: який бомбардувальник атакувати?
Розв’язання. Маємо простий випадок гри 2 х 2; виграш - імовірність неураження носія. Наші стратегії:
А1 — носій — бомбардувальник І;
А2 — носій — бомбардувальник ІІ.
Стратегії супротивника:
B1 — атакується бомбардувальник І; B2 — атакується бомбардувальник ІІ.
Складемо матрицю гри, тобто знайдемо середній виграш при кожній комбінації стратегій.
1. ![]() (носій І,
атакується І).
(носій І,
атакується І).
Носій не буде уражений, якщо бомбардувальники зіб'ють винищувач, або не зіб'ють, але він не вразить свою мету:
= 0,7+ 0,3· 0,4. = 0,82,
2. (носій ІІ, атакується І)
![]() .
.
.
3. (носій І, атакується ІІ)
![]() .
.
4. (носій ІІ, атакується ІІ)
![]()
Матриця гри має вигляд:
|
|
|
|
0,82 |
1 |
|
1 |
0,58 |
Нижня ціна гри 0,82; верхня ціна 1. Матриця не має сідлової точки; розв’язання шукаємо в області змішаних стратегій. Маємо:
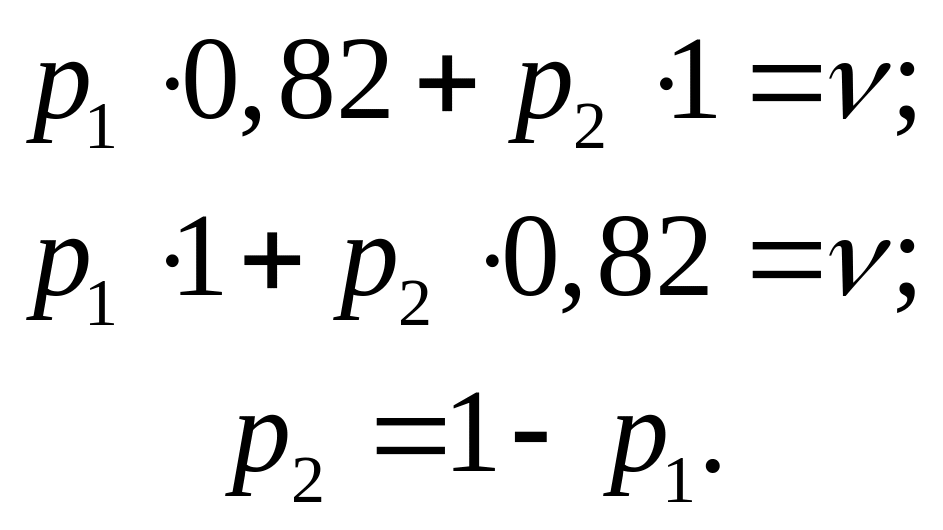
Звідси
![]()
Наша оптимальна стратегія є
![]() .
Тобто в якості носія слід частіше обирати
І. Ціна
гри складає
.
Тобто в якості носія слід частіше обирати
І. Ціна
гри складає
![]() .
.
Знаючи
,
визначаємо
![]() і
і
![]() - частоти стратегій
і
у оптимальній стратегії супротивника
- частоти стратегій
і
у оптимальній стратегії супротивника
![]() .
Маємо:
.
Маємо:
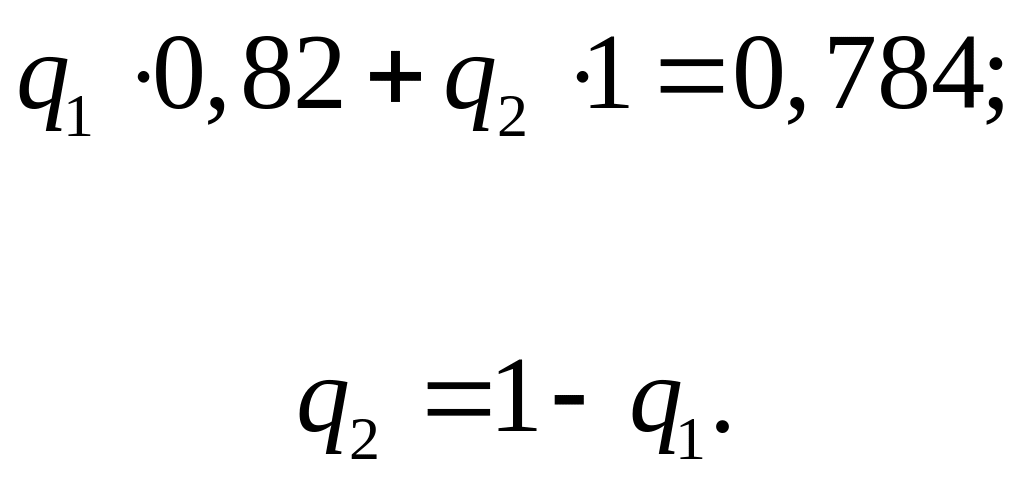
Звідси
![]() ,
,
Тобто оптимальна стратегія
супротивника
![]() .
.
Приклад 4.4. Розв’яжемо геометричним методом задачу знаходження оптимальної змішаної стратегії для наступного прикладу. Розглянемо задачу про поставку сировини. Припустимо, що деяка фірма А уклала договір з іншою фірмою В на поставку сировини, яка швидко псується, щоденно на суму 100 у.о. Якщо впродовж дня сировина не поступає, фірма А несе збитки в розмірі 400 у.о. від простою робітників. Вона може використовувати свій транспорт (додаткові витрати 50 у.о.), але досвід показує, що в половині випадків транспорт повертається порожнім. Можна збільшити ймовірність отримання сировини до 80%, якщо попередньо посилати на фірму В свого представника, але це потребує додаткових витрат у розмірі 40 у.о. Існує можливість замовити денну норму сировини в іншій фірмі за ціною, на 50% вищій, але крім витрат на транспорт (50 у.о.) можливі додаткові витрати в розмірі 30у.о., пов'язані з понаднормованою роботою бригад, які реалізують зайву сировину, якщо в той же день надходить і централізована поставка. Треба побудувати платіжну матрицю, за допомогою якої в подальшому можна буде вибрати оптимальну стратегію фірми А?
Розглянемо можливі стратегії постачальника (фірма В):
- поставка своєчасна;
- поставки немає.
У фірми А згідно з умовою задачі, чотири стратегії:
- не вживати ніяких додаткових заходів;
- послати на фірму В свій транспорт;
- послати на фірму В свого представника і транспорт;
![]() - замовити додаткову сировину
на іншій фірмі.
- замовити додаткову сировину
на іншій фірмі.
Усього можливі 8 ситуацій, які описують всі комбінації з чотирьох стратегій фірми А та двох стратегій фірми В? Ці ситуації та супутні їм збитки і витрати наведено в табл. 1.3.
У загальному випадку, якщо у першого гравця (фірма А) т можливих стратегій, а у другого - n, то завжди створюється т х п можливих ситуацій, кожній з яких відповідає визначений платіж одного гравця другому.
За великої кількості ситуацій табл. 1.3 стає громіздкою й неосяжною, зручніше перейти від неї до платіжної матриці А. Вона є прямокутною матрицею, яка має т рядків (за кількістю стратегій першого гравця) і n стовпчиків (за кількістю стратегій другого гравця).
Таблиця 1.3. Можливі середні денні витрати фірми А
Ситуація |
|
|
Денні витрати фірми А |
|
||
Вар-тість сиро-вини |
Збитки від про-стою |
Транс-портні витрати |
Витрати на від-рядження |
Витрати на понаднор- мовану роботу |
Всього в день |
|
|
100 |
0 |
0 |
0 |
0 |
100 |
|
0 |
400 |
0 |
0 |
0 |
400 |
|
100 |
0 |
50 |
0 |
0 |
150 |
|
50 |
200 |
50 |
0 |
0 |
300 |
|
100 |
0 |
50 |
40 |
0 |
190 |
|
80 |
80 |
50 |
40 |
0 |
250 |
|
250 |
0 |
50 |
0 |
30 |
330 |
|
150 |
0 |
50 |
0 |
0 |
200 |
На перетині i-го рядка j-το стовпчика ставиться платіж другого гравця першому в ситуації, коли застосовується i-та стратегія першим гравцем та j-та стратегія другим. Якщо виграє другий гравець, то платіж буде мати знак мінус.
Платіжна матриця в задачі (грі), яка розглядається, має розмірність 4 x 2 і наведена в табл. 1.4. Усі платежі мають від'ємний знак, оскільки визначають у цій задачі витрати фірми А.
Таблиця 1.4
Стратегії фірми А |
Стратегії фірми В |
|
|
|
|
|
-100 |
-400 |
|
-150 |
-300 |
|
-190 |
-250 |
|
-330 |
-200 |
Платіжна матриця А має вигляд
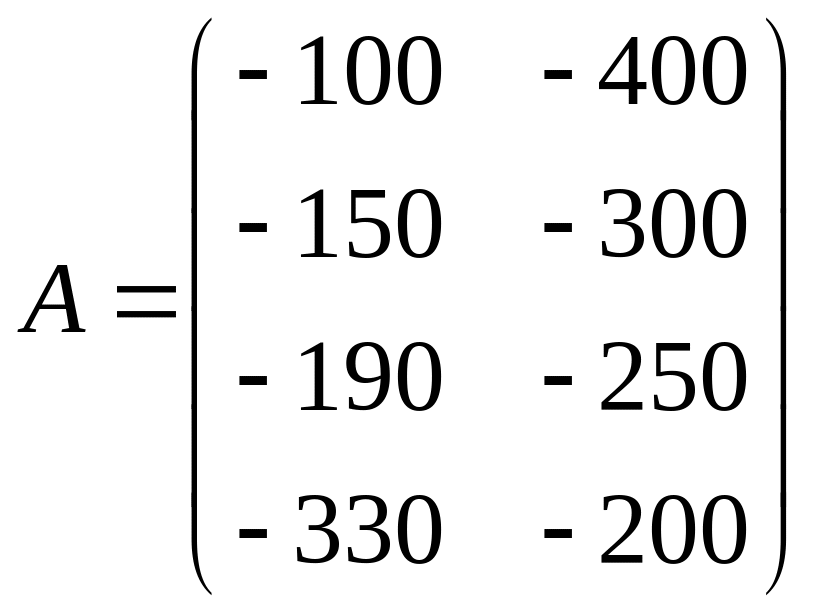
Відкладемо
по горизонтальній осі надійність
постачальника (фірма
В),
яка
вимірюється ймовірностями в діапазоні
0 - 1 і позначимо
її
![]() .
Величина
.
Величина
![]() є,
таким чином, величиною ненадійності
постачальника. Числа
і
є,
таким чином, величиною ненадійності
постачальника. Числа
і
![]() ,
які
дорівнюють в сумі одиниці, показують,
з якою ймовірністю використовуються
постачальником чисті
стратегії
і
в
кожній партії. Сукупність стратегій
і
які
мають
оцінку у вигляді ймовірностей
і
їх
здійснення, буде змішаною
стратегією.
,
які
дорівнюють в сумі одиниці, показують,
з якою ймовірністю використовуються
постачальником чисті
стратегії
і
в
кожній партії. Сукупність стратегій
і
які
мають
оцінку у вигляді ймовірностей
і
їх
здійснення, буде змішаною
стратегією.
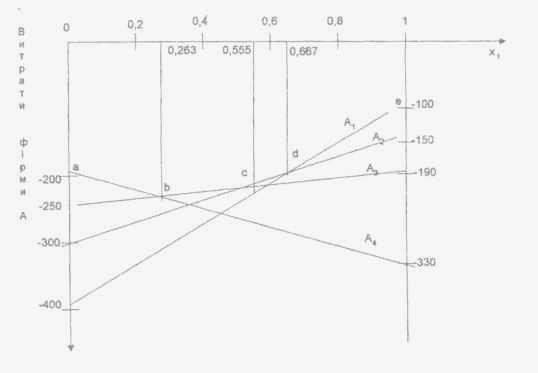
Рис. 4.16. Графіки функцій очікуваних витрат фірми а
Точки
![]() і
і
![]() на
рис. 4.16 відповідають другій і першій
чистим стратегіям
фірми В, а
усі точки
на
рис. 4.16 відповідають другій і першій
чистим стратегіям
фірми В, а
усі точки
![]() всередині відрізка - змішаним
стратегіям. Зрозуміло, що змішаних
стратегій у кожного гравця
нескінченна множина. Побудуємо графіки
очікуваних витрат фірми
А
при
застосуванні своїх чистих стратегій
проти змішаної стратегії
фірми В.
Почнемо
з першої стратегії. Якщо постачальник
абсолютно
надійний (тобто завжди застосовує
стратегію
і
значить
,
всередині відрізка - змішаним
стратегіям. Зрозуміло, що змішаних
стратегій у кожного гравця
нескінченна множина. Побудуємо графіки
очікуваних витрат фірми
А
при
застосуванні своїх чистих стратегій
проти змішаної стратегії
фірми В.
Почнемо
з першої стратегії. Якщо постачальник
абсолютно
надійний (тобто завжди застосовує
стратегію
і
значить
,
![]() ),
витрати фірми А
дорівнюють
відповідно до платіжної матриці -
100 у.о. Відкладемо на графіку точку з
координатами (1; -100). Якщо постачальник
абсолютно ненадійний (тобто завжди
застосовує стратегію
і
значить
,
),
витрати фірми А
дорівнюють
відповідно до платіжної матриці -
100 у.о. Відкладемо на графіку точку з
координатами (1; -100). Якщо постачальник
абсолютно ненадійний (тобто завжди
застосовує стратегію
і
значить
,
![]() ),
то витрати фірми А
дорівнюють
- 400 у.о. і потрібно
відкласти точку з координатами (0; -400).
Якщо надійність фірми
В
,
то щоденні витрати фірми А,
яка
застосовує першу стратегію
проти змішаної стратегії постачальника,
залежать від ймовірності
і
дорівнюють
),
то витрати фірми А
дорівнюють
- 400 у.о. і потрібно
відкласти точку з координатами (0; -400).
Якщо надійність фірми
В
,
то щоденні витрати фірми А,
яка
застосовує першу стратегію
проти змішаної стратегії постачальника,
залежать від ймовірності
і
дорівнюють
![]() у.о. (4.1)
у.о. (4.1)
Графіком цієї функції є пряма лінія (див. рис. 4.16).

 Аналогічно
будуються графіки функцій очікуваних
витрат фірми
при
застосуванні кожної чистої стратегії
проти змішаних стратегій фірми-постачальника
В:
Аналогічно
будуються графіки функцій очікуваних
витрат фірми
при
застосуванні кожної чистої стратегії
проти змішаних стратегій фірми-постачальника
В:
які відповідно позначаються на рис. 4.1 як , , .
При надійності постачальника =0,4 до перетину з лініями функцій очікуваних витрат фірми А з'ясовуємо, що оптимальною буде стратегія А3, яка забезпечує мінімальні витрати - 226 у.о.
Якщо
надійність постачальника
![]() ,
вигідніше застосовувати четверту
стратегію; при надійності постачальника
,
вигідніше застосовувати четверту
стратегію; при надійності постачальника
![]() оптимальною
стратегією буде А3
, при
оптимальною
стратегією буде А3
, при
![]() - А2,
при
- А2,
при![]() -
(див. рис. 4.16).
-
(див. рис. 4.16).
Ці критичні значення надійності отримані із загального розв'язку рівнянь (4.1) - (4.4), які взяті попарно: (4.3) і (4.4) - точка b, (4.2) і (4.3) - точка с (4.1) і (4.2) - точка d.
Наведена ламана лінія abcde показує, як змінюються витрати фірми А при зміні надійності постачальника від 0 до 1. Як видно з графіка, збільшення надійності постачальника не призводить автоматично до зменшення витрат фірми А. Справді, коли надійність постачальника зростає від 0 до 0,263, витрати фірми А зростають від —200 у.о. до
![]()
Збільшення витрат зумовлено тим, що сировина закуповується у другого постачальника, а нерегулярні поставки основного постачальника (з ймовірністю 0,263) призводять до додаткових витрат.
При надійності постачальника = 0,263 витрати фірми А максимальні з усіх можливих при розумному виборі фірмою А своїх стратегій (цей максимум залежить від величин умовно-вибраних витрат (див. табл. 4.1)).
Якби гра була б антагоністичною, тобто постачальник прагнув нанести фірмі А максимальний збиток, його оптимальна надійність повинна була б дорівнювати = 0,263. При цьому витрати фірми А становили б — 234,2 у.о. і оптимальними були б стратегії і (точка b знаходиться на перетині ліній і ). Справді, підставляючи = 0,263 в рівняння (4.3), (4.4), отримаємо S3(0,236) = S4(0,236) = -234,2 у.о.
У зв'язку з тим, що фірма-постачальник прагне нанести фірмі А максимальний збиток, остання не може вибирати якусь одну з чистих стратегій А3 або А4 бо в цьому випадку, якщо фірма В змінить надійність поставок у меншу сторону від = 0,263 (у випадку стратегії А3) або в більшу сторону (у випадку стратегії А4) збитки зростуть і будуть більші, ніж -234,2 у.о.
Оскільки в антагоністичній грі перша і друга стратегії фірми А неефективні, розглянемо можливість знаходження змішаної стратегії А3 і А4 з такими ймовірностями застосування, при яких збитки фірми А були б не більшими -234,2 у.о. при будь-яких стратегіях фірми В.
Побудуємо графіки витрат фірми А, яка застосовує свою змішану стратегію і складається з чистих стратегій А3 і А4 проти кожної чистої стратегії В1 і В2 фірми В (рис. 4.17).
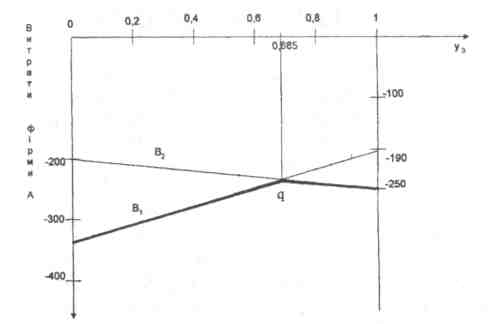
Рис. 4.17. Графіки очікуваних витрат фірми А в антагоністичній грі.
Позначимо через Y3 ймовірність застосування стратегії А3 а через Y4 - стратегії А4 (Y3 + Y4 = 1). З графіка, побудованого аналогічно графіку на рис.4.17, видно, що оптимальна змішана стратегія фірми А включає стратегії А3 і А4 , які застосовуються з ймовірностями Y3= 0,685 і Y4= 0,315.
Оптимальні
витрати фірми А
(які
називаються у випадку антагоністичної
гри ціною
гри) дорівнюють
ординаті точки перетину q.
Підставляючи
Y3=0,685
у будь-яке із рівнянь прямих
![]() ,
отримуємо те саме значення витрат
-234,2 у.о., яке було розраховано раніше.
Нарис. 4.2 видно, що в
антагоністичній грі фірмі А
не
слід відступати від своєї оптимальної
змішаної
стратегії Y1
= Y2
= 0;
Y3
= 0,685; Y4
= 0,315, оскільки витрати збільшуються
(у напрямку наведених ліній). При Y3<
0,685 фірма В
почне
застосовувати чисту стратегію
при
Y3>
0,685 - чисту стратегію В2
і
нанесе фірмі А
збитки
більші, ніж -234,2 у.о.
,
отримуємо те саме значення витрат
-234,2 у.о., яке було розраховано раніше.
Нарис. 4.2 видно, що в
антагоністичній грі фірмі А
не
слід відступати від своєї оптимальної
змішаної
стратегії Y1
= Y2
= 0;
Y3
= 0,685; Y4
= 0,315, оскільки витрати збільшуються
(у напрямку наведених ліній). При Y3<
0,685 фірма В
почне
застосовувати чисту стратегію
при
Y3>
0,685 - чисту стратегію В2
і
нанесе фірмі А
збитки
більші, ніж -234,2 у.о.
Таким чином, якби гра була антагоністична (тобто кожний гравець наносить супротивнику максимальний збиток), гравцям необхідно рекомендувати такі оптимальні стратегії: фірмі А – Y1 = Y2 = 0; Y3 = 0,685, Y4 = 0,315; фірмі В - = 0,263, = 0,737. При цьому вартість гри (тобто очікувані збитки фірми А) дорівнює - 234,2 у.о.
