2.Градиент и его свойства

Пусть n-мерный вектор, здесь символом «′» обозначена операция транспозиции, которая превращает строки в столбцы и столбцы в строки, так что

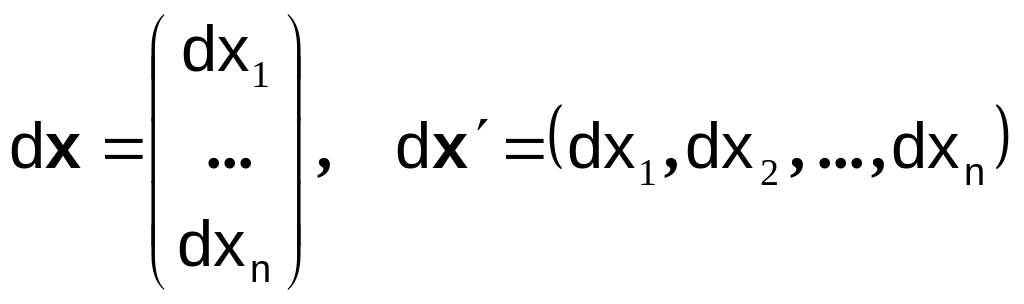
а F(x) – непрерывно дифференцируемая функция переменной x , т.е. F(x) функция n переменных x_i. Градиентом F(x) в точке x₀ называется n-мерный вектор-столбец = , координатами которого являются частные производные F(x) по координатам x_i, вычисленные в некоторой точке x₀.

Основные свойства:

1. Используя вектор-градиент можно записать первый дифференциал в виде скалярного произведения:

dF= ( dx) = │dx│ cos φ

Здесь cos φ это косинус угла между вектором смещения dx и градиентом. Из такой формы записи следует несколько выводов:

2. Производная по любому направлению равна проекции градиента на это направление: т.е. произведению длины градиента на косинус угла между градиентом и вектором направления

3. Вектор градиент всегда направлен в сторону скорейшего возрастания функций.

4. В направлении перпендикулярном градиенту производная равна нулю. Поэтому градиент функции F всегда перпендикулярен к линии уровня этой функции.

5. Для линейной функции F(х) = c₁ x₁ + c₂ x₂ +.... c_n x_n = (cx) градиентом является постоянный вектор коэффициентов (c₁, c₂,.... c_n)′= c т.е. линейная функция быстрее всего растет в направлении c , и вообще растет только в тех направлениях, на которые c имеет положительную проекцию.

3. Первый дифференциал

Пусть функция многих переменных F(x) в окрестности точки x₀ имеет непрерывные производные по всем переменным, тогда F(x) называется дифференцируемой в точке x₀ , втом и только в том случае когда ее приращение имеет вид суммы линейной формы А₁х₁ + А₂х₂ + … + А_nх_n и некоторой ошибки , которая есть бесконечно малая более высокого порядка, чем dr:  = o(dr); далее будем обозначать как . Получим, что функция дифференцируема в точке тогда и только тогда, когда для ее приращения справедливо пердставление :

F=F(x₀+dx)– F(x₀) = А₁dх₁ + А₂dх₂ + … + А_ndх_n + = dF(x₀) +

При этом линейна часть приращения называется первым дифференциалом:

dF(x₀) = А₁dх₁ + А₂dх₂ + … + А_ndх_n

По определению i–й коэффициент А_i в формуле первого дифференциала называется частной производной функции F в точке x₀ по переменной х_i .

dF(x₀) = dx₁ + dx₂ + …+ dx_n

Вполне очевидно, что первый дифференциал может быть представленр в виде скалярного произведения вектора-градиента = на вектор смещения dF(x₀) = ( dx)

4. Частные производные второго порядка

Если в некоторой области у F(х) существуют частные производные первого порядка, их самих можно рассматривать как функции, и у них могут существовать свои производные. Если, например, пространство трехмерно: , , то производная функции по второй переменной есть в свою очередь функция всех трех переменных . Соответственно, она может иметь три частных производных:

При этом производная во второй строке называется чистой второй производной, а остальные смешанными.

Если функция F(х) обладает всеми производными второго порядка, то можно построить матрицу вторых частных производных (матрицу Гессе или гессиан) по столбцам которой стоят градиенты первых частных производных

Важное свойство:

У дифференцируемых функций вторые смешанные частные производные не зависят от порядка дифференцирования: = , а значит МАТРИЦА ГЕССЕ ВСЕГДА СИММЕТРИЧНА