- •III семестр. Ммф нгу
- •Конспект лекций1
- •2003 – 2004 Учебный год
- •Содержание
- •Лекция 1. Традиционные задачи линейной алгебры
- •Векторные и матричные нормы
- •Число обусловленности
- •Лекция 2. Прямые методы решения линейных уравнений Метод исключения Гаусса – схема единственного деления
- •Теорема об lu разложении
- •Разложение Холесского
- •Метод квадратного корня
- •Метод вращений решения системы уравнений Элементарная матрица вращения
- •–Ый шаг метода вращений
- •Решение системы с вырожденной матрицей –разложение с перестановками столбцов матрицы
- •Совместность системы с вырожденной матрицей
- •Применение –разложения с перестановками столбцов для решения совместной системы
- •Метод прогонки решения систем с трехдиагональной матрицей –разложение трехдиагональной матрицы :
- •Формулы метода прогонки для системы :
- •Асимптотическая скорость сходимости
- •Метод Зейделя (Гаусса–Зейделя, Некрасова)
- •Необходимое и достаточное условие сходимости метода Зейделя в случае симметричной матрицы с положительной главной диагональю
- •Лекция 7. Функционал ошибки
- •Метод полной релаксации
- •Метод неполной релаксации
- •Метод минимальных невязок
- •Метод простой итерации
- •Оценки сходимости мнс и ммн
- •Лекция 9. Метод Ричардсона с чебышевскими параметрами Задача оптимизации параметров
- •Полином Чебышева и решение задачи оптимизации параметров
- •Циклический метод Ричардсона: формулы и сходимость
- •Об устойчивости метода Ричардсона
- •Трехчленные формулы реализации метода Ричардсона с чебышевскими параметрами
- •Лекция 10. Многошаговые методы. Вариационная оптимизация
- •Метод сопряженных градиентов
- •Переобуславливатель
- •Положительно определенные матрицы
- •Лекция 11. Проблема собственных значений
- •Корректность задачи на собственные значения
- •Степенной метод вычисления максимального собственного значения матрицы
- •Степенной метод вычисления минимального собственного значения матрицы
- •Применение ортогонализации и степенного метода для вычисления очередного собственного значения
- •Лекция 12. Метод деления пополам (бисекций)
- •Идея метода бисекций вычисления
- •Приведение самосопряженной матрицы к трехдиагональному виду ортогональным преобразованием подобия с помощью матриц вращения
- •Якобиевы матрицы
- •О вычислении чпз
- •О вычислении собственного вектора
- •Лекция 13. Метод вращений (Якоби)
- •Выбор вращения
- •Сходимость собственных значений
- •Сходимость собственных векторов
- •Литература
Циклический метод Ричардсона: формулы и сходимость
Теорема. |
Если
и известны оценки ее спектра:
с
чебышевскими параметрами
сходится
и
|
Об устойчивости метода Ричардсона
Из–за
ошибок округления реализация формул
![]() неустойчива, т.к. норма оператора шага
неустойчива, т.к. норма оператора шага
![]() для ошибки может быть значительно больше
1 (в методе простой итерации эта норма
меньше 1).
для ошибки может быть значительно больше
1 (в методе простой итерации эта норма
меньше 1).
Рассмотрим
модельный пример, в котором ошибка
округления возникает только на шаге с
![]() (
(![]() ):
):

Проверить:
![]()
![]() .
.
Проверить:
![]() ,
,

![]() ,
если
,
если
![]() ,
т.е. фактически ошибка не уменьшилась.
,
т.е. фактически ошибка не уменьшилась.
Изменим
упорядочение параметров:
![]() :
:
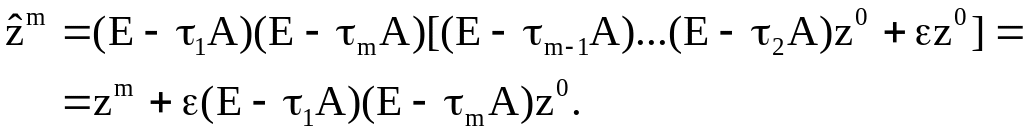
Проверить:
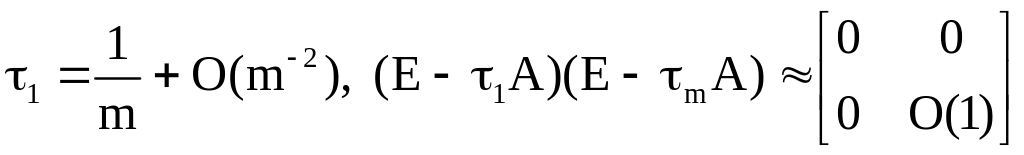
![]() ,
,
т.е. реализация с точностью до ошибок округления.
Из этого примера следует, что переупорядочение параметров существенно влияет на устойчивость вычислений в методе Ричардсона. Задача об оптимальном упорядочении параметров ставится следующим образом.
Пусть |
|
Найти |
|
Решением
этой задачи для
![]() является следующая процедура:
является следующая процедура:
![]()
![]()
![]()
![]()
![]()
![]()
Трехчленные формулы реализации метода Ричардсона с чебышевскими параметрами
Для решения
системы
![]() попытаемся построить приближения
попытаемся построить приближения
![]() :
:
![]() .
.
Т.к.
![]() и
и
 (проверить!), то
(проверить!), то
 .
.
Если
ввести обозначение
![]() ,
то
,
то
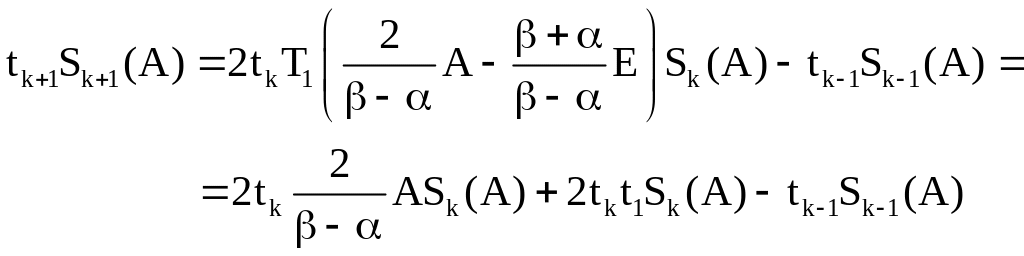
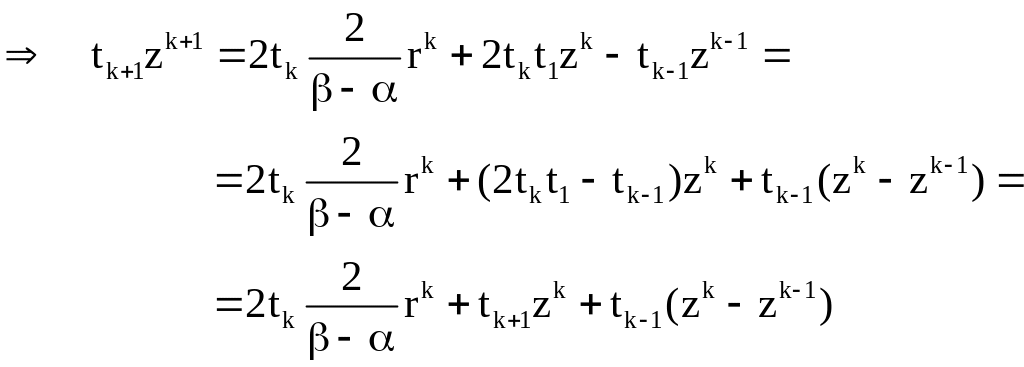

![]() построена:
построена:

Преобразуем эту формулу:
 .
.
Введем
обозначение
![]() ,
т.к.
,
т.к.
![]() ,
то
,
то

Тогда
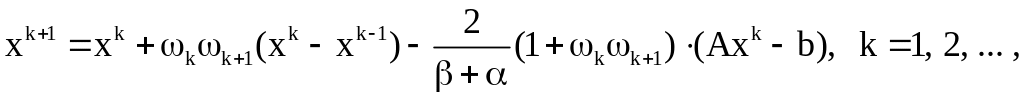
– двухшаговый (трехслойный) итерационный процесс.
Лекция 10. Многошаговые методы. Вариационная оптимизация
Для
определения параметров метода Ричардсона
(простой итерации при
![]() )
для решения системы
необходимо предварительное вычисление
(точное или приближенное) границ спектра
матрицы
)
для решения системы
необходимо предварительное вычисление
(точное или приближенное) границ спектра
матрицы
![]() ,
чего не требуется в методах наискорейшего
спуска и минимальных невязок. Попытаемся
выбрать параметры метода
,
чего не требуется в методах наискорейшего
спуска и минимальных невязок. Попытаемся
выбрать параметры метода
![]() из условия
из условия
![]() .
.
Решим эту
задачу при
![]() (т.к. при других
(т.к. при других
![]() решение задачи будет таким же с точностью
до обозначений), определив
решение задачи будет таким же с точностью
до обозначений), определив
![]() ,
где
,
где
![]() .
.
Т.к.

где
![]() ,
,
то
![]() .
.
Параметры
![]() удовлетворяют системе уравнений
удовлетворяют системе уравнений
 ,
,
или
 .
.
Матрица
этой системы – матрица Грамма базиса
![]() в
в
![]() .
.
Для того,
чтобы был известен вектор правой части,
достаточно выбрать
![]() с любой матрицей
с любой матрицей
![]() .
.
Если базис
является
![]() –ортогональным,
т.е.
–ортогональным,
т.е.
![]() ,
то
,
то
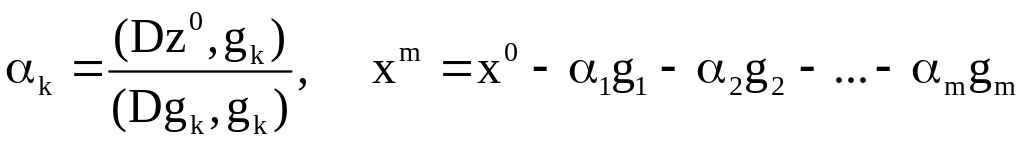 ,
,
а вычисление
![]() осуществляется аналогично.
осуществляется аналогично.
Метод сопряженных градиентов
Пусть
матрица системы
![]() симметрична и положительно определена.
Построим (
симметрична и положительно определена.
Построим (![]() )
)
![]() –ортогональный
базис
в
–ортогональный
базис
в
![]() .
.
1.
– базис
в
|
|
|
Заметим, что
|
Предположим,
что выполнили
Определим
т.е.
Заметим,
что
|
|
– базис
в
|
|
т.к.
Т.к.
и
мы построили метод сопряженных градиентов. |
|
Теорема.
Если
![]() ,
то метод сопряженных градиентов
продолжается до получения решения
системы
за
,
то метод сопряженных градиентов
продолжается до получения решения
системы
за
![]() итераций (пока
итераций (пока
![]() )
и
)
и
 .
.
Доказать теорему в качестве упражнения.



 .
. ,
,
 .
.