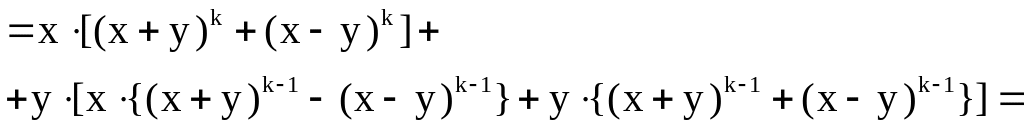- •III семестр. Ммф нгу
- •Конспект лекций1
- •2003 – 2004 Учебный год
- •Содержание
- •Лекция 1. Традиционные задачи линейной алгебры
- •Векторные и матричные нормы
- •Число обусловленности
- •Лекция 2. Прямые методы решения линейных уравнений Метод исключения Гаусса – схема единственного деления
- •Теорема об lu разложении
- •Разложение Холесского
- •Метод квадратного корня
- •Метод вращений решения системы уравнений Элементарная матрица вращения
- •–Ый шаг метода вращений
- •Решение системы с вырожденной матрицей –разложение с перестановками столбцов матрицы
- •Совместность системы с вырожденной матрицей
- •Применение –разложения с перестановками столбцов для решения совместной системы
- •Метод прогонки решения систем с трехдиагональной матрицей –разложение трехдиагональной матрицы :
- •Формулы метода прогонки для системы :
- •Асимптотическая скорость сходимости
- •Метод Зейделя (Гаусса–Зейделя, Некрасова)
- •Необходимое и достаточное условие сходимости метода Зейделя в случае симметричной матрицы с положительной главной диагональю
- •Лекция 7. Функционал ошибки
- •Метод полной релаксации
- •Метод неполной релаксации
- •Метод минимальных невязок
- •Метод простой итерации
- •Оценки сходимости мнс и ммн
- •Лекция 9. Метод Ричардсона с чебышевскими параметрами Задача оптимизации параметров
- •Полином Чебышева и решение задачи оптимизации параметров
- •Циклический метод Ричардсона: формулы и сходимость
- •Об устойчивости метода Ричардсона
- •Трехчленные формулы реализации метода Ричардсона с чебышевскими параметрами
- •Лекция 10. Многошаговые методы. Вариационная оптимизация
- •Метод сопряженных градиентов
- •Переобуславливатель
- •Положительно определенные матрицы
- •Лекция 11. Проблема собственных значений
- •Корректность задачи на собственные значения
- •Степенной метод вычисления максимального собственного значения матрицы
- •Степенной метод вычисления минимального собственного значения матрицы
- •Применение ортогонализации и степенного метода для вычисления очередного собственного значения
- •Лекция 12. Метод деления пополам (бисекций)
- •Идея метода бисекций вычисления
- •Приведение самосопряженной матрицы к трехдиагональному виду ортогональным преобразованием подобия с помощью матриц вращения
- •Якобиевы матрицы
- •О вычислении чпз
- •О вычислении собственного вектора
- •Лекция 13. Метод вращений (Якоби)
- •Выбор вращения
- •Сходимость собственных значений
- •Сходимость собственных векторов
- •Литература
Метод минимальных невязок
В
итерационном процессе
параметр
![]() будем выбирать из условия минимизации
невязки:
будем выбирать из условия минимизации
невязки:
![]() .
.
Теорема. |
Метод минимальных невязок сходится , если . |
|
Док–во. |
минимум
правой части достигается при
Очевидно, что оператор : непрерывен всюду, кроме , быть может, 0. . |
|
Метод простой итерации
В методах
наискорейшего спуска и минимальных
невязок для определения параметра
![]() на каждом шаге нужно вычислять два
скалярных произведения (с умножением
невязки на матрицу системы). Использование
постоянного параметра
на каждом шаге нужно вычислять два
скалярных произведения (с умножением
невязки на матрицу системы). Использование
постоянного параметра
![]() существенно уменьшает объем вычислений
на каждом шаге.
существенно уменьшает объем вычислений
на каждом шаге.
Теорема. |
Если
метод простой итерации сходится при
|
|
|
|
|||
|
При
|
||
Док–во. |
|
||
|
т.к.
функция
Оптимальный параметр выбираем из условия
легко проверить, что
|
||
Оценки сходимости мнс и ммн
Теорема. |
Если
,
то для ошибки
справедливы оценки: |
Док-во. |
Так как |
|
и
то
Т.к.
то
|
Теорема. |
Если , то для метода минимальных невязок:
справедливы оценки: |
Док-во. |
Так как |
|
и
Т.к.
|
Лекция 9. Метод Ричардсона с чебышевскими параметрами Задача оптимизации параметров
Параметры
в итерационном методе
![]() можно выбирать из условия минимизации
спектрального радиуса
можно выбирать из условия минимизации
спектрального радиуса
![]() матрицы (оператора) ошибки за
матрицы (оператора) ошибки за
![]() шагов:
шагов:
![]() .
.
Если все параметры взять одинаковыми, то мы получим метод простой итерации и он сходится при известных условиях, т.е. предлагаемый способ построения итерационного метода может привести только к лучшему методу.
Мы будем
предполагать, что
![]() ,
т.е. все собственные значения матрицы
системы линейных уравнений
положительны.
,
т.е. все собственные значения матрицы
системы линейных уравнений
положительны.
Т.к.
![]() ,
а последнюю минимаксную задачу решать
проще (почему?), мы будем искать
,
а последнюю минимаксную задачу решать
проще (почему?), мы будем искать
![]() :
:
![]() ,
,
т.е. решать
задачу о поиске полинома
![]() степени
степени
![]() ,
наименее уклоняющегося от нуля на
отрезке
,
наименее уклоняющегося от нуля на
отрезке
![]() при условии
при условии
![]() .
.
Тогда,
т.к.
 ,
где
,
где
![]() – корни полинома
,
– корни полинома
,
 и
и
![]() .
.
Если
![]() ,
то
,
то
![]() и, следовательно,
и, следовательно,
![]()
– оценка сходимости метода.
Полином Чебышева и решение задачи оптимизации параметров
Очевидно,
что
![]() ,
,
![]() – полиномы.
– полиномы.
Т.к.
![]() ,
то при
,
то при
![]() имеем
имеем
![]() – полином при любом
– полином при любом
![]() .
.
Точки
экстремумов
![]() :
:
![]() :
:
![]() ,
,
![]() .
.
Корни
полинома
:
![]() :
:
![]() ,
,
![]() .
.
Линейное
преобразование
![]() :
:
 .
.
Рассмотрим
полином:
 .
.
Очевидно,
что
![]() ,
,
![]() – корни полинома.
– корни полинома.
Покажем,
что этот полином наименее уклоняется
от нуля на интервале
среди всех полиномов
![]() ,
т.е.
,
т.е.
![]() .
.
Теорема. |
Если
|
Док-во. |
Пусть
тогда
Так как
то
разность
Следовательно, . |
Осталось
вычислить
![]() .
.
Теорема. |
Если
,
то
|
Док-во. |
Очевидно,
Для
вычисления
|
|
Заметим, что
Тогда
Док-во
формулы
Действительно, и . Осталось проверить, что или
Пусть
|
Итак,
![]() – решение задачи оптимизации параметров
за
шагов.
– решение задачи оптимизации параметров
за
шагов.



 ,
если
,
если
 ,
,
 .
.

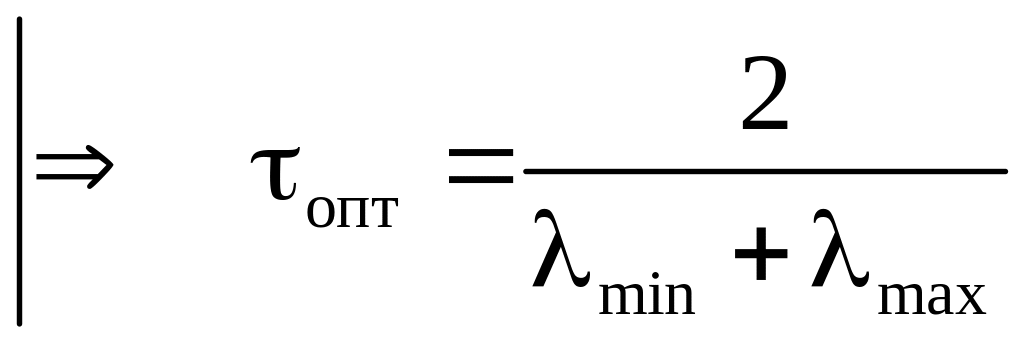 ,
,


 ,
,


 ,
,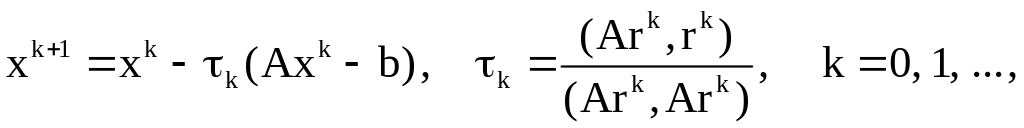
 ,
,

 .
. ,
,
 ,
где
,
где
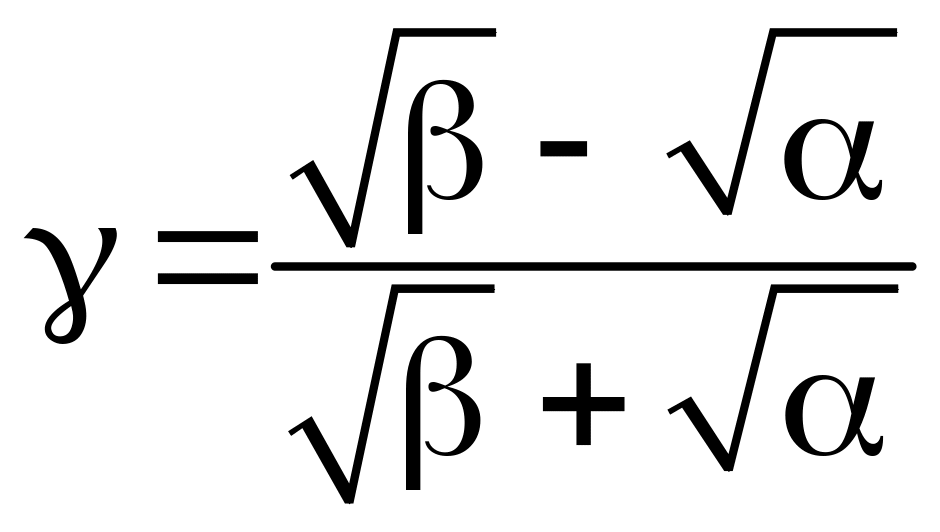 .
. .
. при
при

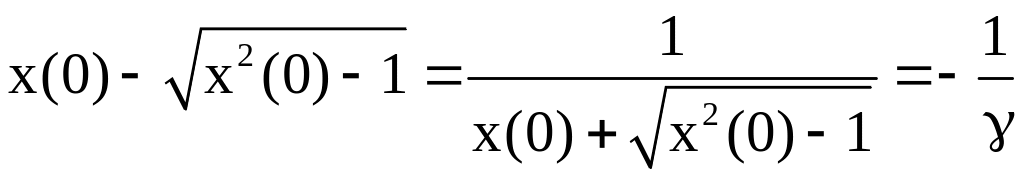 .
. .
.