
- •III семестр. Ммф нгу
- •Конспект лекций1
- •2003 – 2004 Учебный год
- •Содержание
- •Лекция 1. Традиционные задачи линейной алгебры
- •Векторные и матричные нормы
- •Число обусловленности
- •Лекция 2. Прямые методы решения линейных уравнений Метод исключения Гаусса – схема единственного деления
- •Теорема об lu разложении
- •Разложение Холесского
- •Метод квадратного корня
- •Метод вращений решения системы уравнений Элементарная матрица вращения
- •–Ый шаг метода вращений
- •Решение системы с вырожденной матрицей –разложение с перестановками столбцов матрицы
- •Совместность системы с вырожденной матрицей
- •Применение –разложения с перестановками столбцов для решения совместной системы
- •Метод прогонки решения систем с трехдиагональной матрицей –разложение трехдиагональной матрицы :
- •Формулы метода прогонки для системы :
- •Асимптотическая скорость сходимости
- •Метод Зейделя (Гаусса–Зейделя, Некрасова)
- •Необходимое и достаточное условие сходимости метода Зейделя в случае симметричной матрицы с положительной главной диагональю
- •Лекция 7. Функционал ошибки
- •Метод полной релаксации
- •Метод неполной релаксации
- •Метод минимальных невязок
- •Метод простой итерации
- •Оценки сходимости мнс и ммн
- •Лекция 9. Метод Ричардсона с чебышевскими параметрами Задача оптимизации параметров
- •Полином Чебышева и решение задачи оптимизации параметров
- •Циклический метод Ричардсона: формулы и сходимость
- •Об устойчивости метода Ричардсона
- •Трехчленные формулы реализации метода Ричардсона с чебышевскими параметрами
- •Лекция 10. Многошаговые методы. Вариационная оптимизация
- •Метод сопряженных градиентов
- •Переобуславливатель
- •Положительно определенные матрицы
- •Лекция 11. Проблема собственных значений
- •Корректность задачи на собственные значения
- •Степенной метод вычисления максимального собственного значения матрицы
- •Степенной метод вычисления минимального собственного значения матрицы
- •Применение ортогонализации и степенного метода для вычисления очередного собственного значения
- •Лекция 12. Метод деления пополам (бисекций)
- •Идея метода бисекций вычисления
- •Приведение самосопряженной матрицы к трехдиагональному виду ортогональным преобразованием подобия с помощью матриц вращения
- •Якобиевы матрицы
- •О вычислении чпз
- •О вычислении собственного вектора
- •Лекция 13. Метод вращений (Якоби)
- •Выбор вращения
- •Сходимость собственных значений
- •Сходимость собственных векторов
- •Литература
Число обусловленности
Определение.
![]()
1.
|
2.
|
Теорема. |
|
Док–во. |
|
Теорема. |
|
Док–во. |
1.
2. Т.к.
|
Лекция 2. Прямые методы решения линейных уравнений Метод исключения Гаусса – схема единственного деления

Схема единственного деления на примере системы третьего порядка:
Прямой ход: |
Матричная формулировка: |
|
|
|
|
|
|
|
|
|
|
|
|
|
Обратный ход:
|
Матричная формулировка:
|
|
Формулы схемы единственного деления (доказать):
k–ый шаг прямого хода:
|
|
Теорема об lu разложении
Если
![]() ,
то
,
то
![]() ,
где
,
где
![]() – нижняя,
– нижняя,
![]() – верхняя треугольные матрицы.
– верхняя треугольные матрицы.
Доказательство.
Если
![]() ,
то
,
то
![]() ,
,
![]() ,
,
т.к.
 .
.
Предположим,
что разложение
найдено (![]() ).
Вычислим
).
Вычислим
![]()
(т.е.
последние строку матрицы
![]() и столбец матрицы
и столбец матрицы
![]() ):
):
т.к.

то
 – системы с треугольными неособенными
матрицами (решения
– системы с треугольными неособенными
матрицами (решения
![]() ),
и
),
и
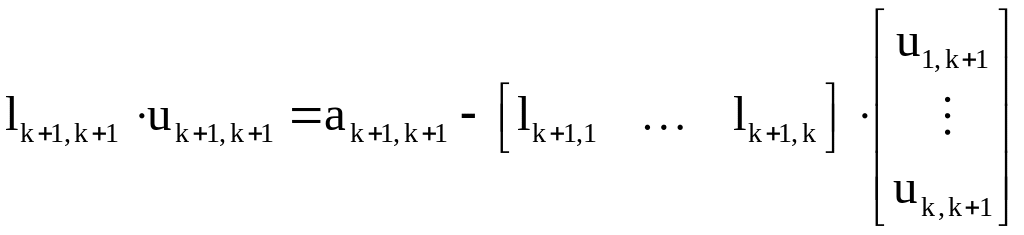 ,
,
очевидно, что решение этого уравнения существует, но не единственно.
(так как
![]() ,
то
,
то
![]() .)
.)
И, наконец,
![]() .
.
Объем вычислений.
Так как
для решения системы уравнений с
треугольной матрицей порядка
![]() достаточно выполнить
достаточно выполнить
![]() умножений и делений, то полагая на каждом
шаге
умножений и делений, то полагая на каждом
шаге
![]() ,
получим, что число таких операций для
вычисления последних строки и столбца
матриц
и
равно
,
получим, что число таких операций для
вычисления последних строки и столбца
матриц
и
равно
![]() ,
а для вычисления матриц
,
а для вычисления матриц
![]() и
и
![]() достаточно
достаточно
![]() умножений или делений.
умножений или делений.
Замечание.
Если
построено
![]() –разложение
матрицы
–разложение
матрицы
![]() ,
то ее определитель вычисляется за
,
то ее определитель вычисляется за
![]() умножений (перемножаются диагональные
(ведущие) элементы).
умножений (перемножаются диагональные
(ведущие) элементы).
Теорема (об
Если
то
разложение
|
Док–во. Пусть
(т.к.
|
Разложение Холесского
Теорема. |
Если
то
|
Док–во. |
Т.к.
Т.к.
|
Метод квадратного корня
Теорема. |
Если
,
то
|
Док–во. |
Из теоремы о разложении Холесского имеем
Т.к.
Аналогично
|
Решение
системы уравнений
с помощью разложения
![]() называется методом квадратного корня.
Так как
называется методом квадратного корня.
Так как

![]()
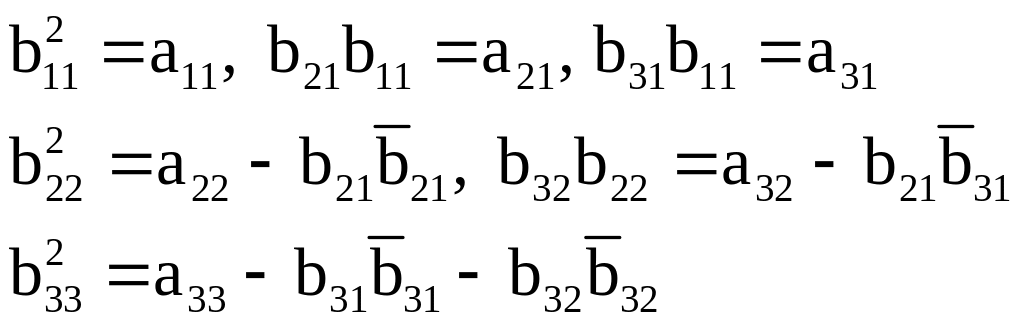
то элементы матрицы B вычисляются по следующим формулам:

Лекция 3.
Метод исключения с выбором главного элемента по столбцу
Напомним 1–ый шаг схемы единственного деления для решения :
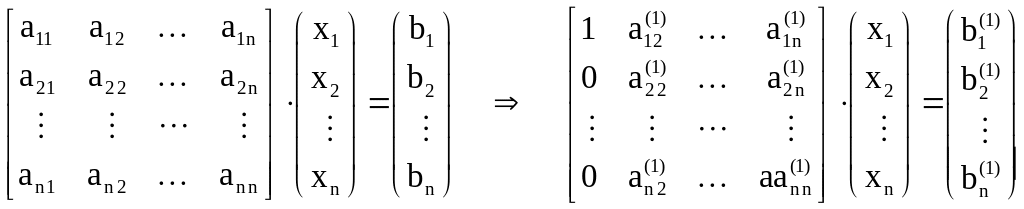 ,
,
где
![]() ,
,
![]() .
.
Эти
операции выполнимы, если (главный элемент
шага)
![]() .
.
Ошибки
округления будут меньше, если
![]() или
или
![]() .
.
Матрица перестановок
 ,
где
,
где
![]() – перестановка
– перестановка
![]() .
.
Доказать,
что
![]() ,
т.е.
,
т.е.
![]() – ортогональная матрица.
– ортогональная матрица.
Доказать,
что
![]() .
.
Элементарная матрица перестановок
![]() – матрица
перестановок
и
– матрица
перестановок
и
![]() элементов в
элементов в
![]() –ке
.
–ке
.
Доказать,
что
![]() .
.
Доказать,
что умножение на матрицу
![]() матрицы
слева (
матрицы
слева (![]() )
– это перестановка
и
строк, справа (
)
– это перестановка
и
строк, справа (![]() )
–перестановка
и
столбцов матрицы
.
)
–перестановка
и
столбцов матрицы
.
Выбор главного элемента по столбцу.
1–й шаг: |
находим
меняем
местами 1 и
обнуляем
в 1–ом столбце элементы:
|
После
шагов имеем
![]() ,
где
,
где
![]() ,
если
,
если

(![]() )–й
шаг:
)–й
шаг:
|
находим
меняем
местами
и
обнуляем в ( )–ом столбце элементы:
|
Очевидно,
что, если
,
то выполнив
![]() шаг, получим систему с верхней треугольной
матрицей:
шаг, получим систему с верхней треугольной
матрицей:
![]() .
.
Теорема. |
Если
,
то
|
Доказать
эту теорему в качестве упражнения,
проверив, что матрицы
![]() и
и
![]() имеют одинаковую структуру.
имеют одинаковую структуру.



 .
.
 ,
т.к.
,
т.к.






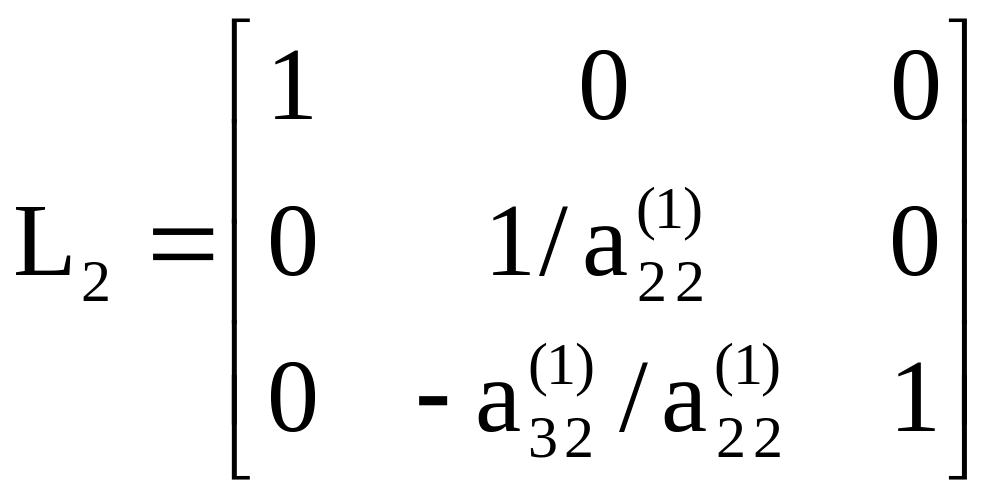



 ,
,


 ,
то
,
то
 ,
,

 ,
,
 ,
,
 ,
,
 .
.