4. Контрольные вопросы

1. Получить выражение для погрешности интегрирования интегрирующей RL-цепи.

2. 

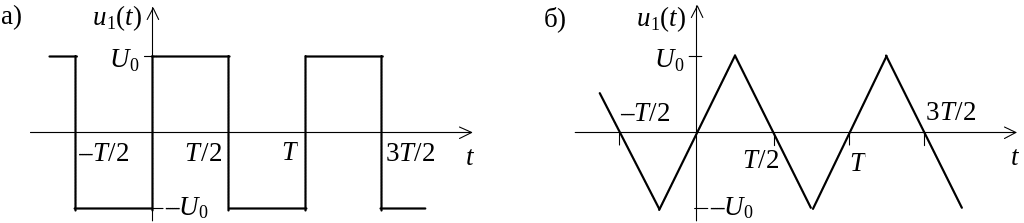
   Рис. 6. Прямоугольный (а) и пилообразный (б) входные сигналы

   Нарисовать сигналы на выходе идеальных дифференциатора и интегратора, если на их входы подается меандр с периодом T (рис. 6, а).

3. Нарисовать сигналы на выходе идеальных дифференциатора и интегратора, если на их входы подается периодическое пилообразное напряжение с периодом T (рис. 6, б).

4. Какой из сигналов, показанных на рис. 6, удобнее использовать в качестве входного при оценке качества работы интегрирующей и дифференцирующей цепей?

5. Какую форму будут иметь сигналы на выходах интегрирующей и дифференцирующей цепей при подаче на их входы синусоидального напряжения?

6. В какой RC-цепи – интегрирующей или дифференцирующей – влияние емкостной нагрузки оказывается более сильным? Почему?

Лабораторная работа № 4 пассивные фильтры

Цель работы: Знакомство со схемами пассивных RC-фильтров, расчет и измерение их частотных характеристик.

1. Теоретические сведения

Фильтром называется линейный четырехполюсник, пропускающий с минимальным ослаблением сигналы, частота которых лежит в пределах полосы пропускания фильтра, и максимально ослабляющий сигналы, частота которых лежит в пределах полосы подавления фильтра. Частоты, определяющие границы полосы пропускания, _н и _в называют соответсвенно нижней и верхней частотами среза. Как и всякий линейный четырехполюсник, фильтр можно характеризовать его частотной характеристикой K(j), модуль которой называется амплитудно-частотной характеристикой (АЧХ) фильтра, а аргумент – фазочастотной характеристикой (ФЧХ). Помимо АЧХ, при исследовании фильтров применяют коэффициент затухания (), который определяется как

(1)

и измеряется в децибелах (дБ).

Фильтры могут быть реализованы как на основе пассивных радиотехнических элементов – резисторов, конденсаторов и катушек индуктивности, так и с применением активных элементов – транзисторов и операционных усилителей. В данной лабораторной работе исследуются пассивные RC-фильтры четырех типов – фильтры нижних и верхних частот, полосовые и режекторные фильтры.

1.1. Фильтр нижних частот

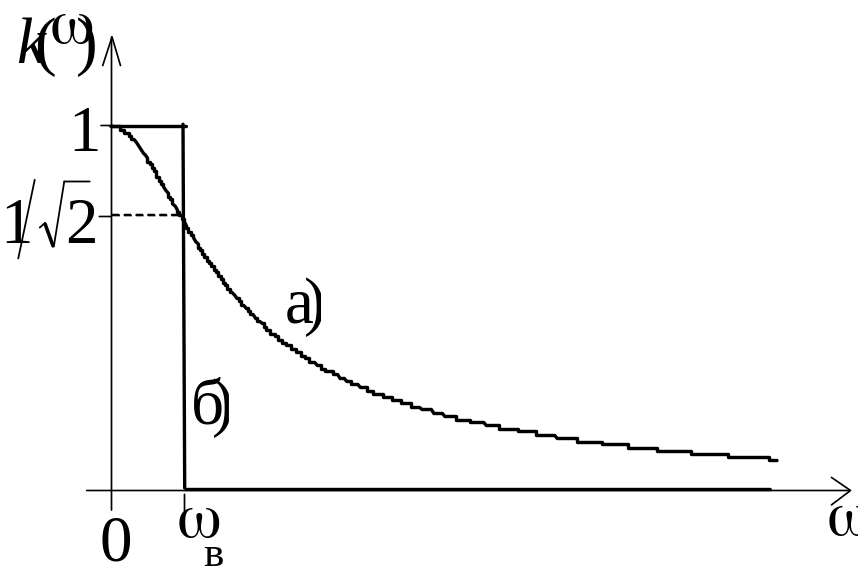
АЧХ идеального фильтра нижних частот (ФНЧ) имеет вид

и характеризуется только одной (верхней) частотой среза. АЧХ реального ФНЧ в полосе пропускания непостоянна, а в полосе подавления – не равна нулю, поскольку переход от полосы пропускания к полосе подавления плавный. При этом частотой среза реального ФНЧ принято считать частоту, на которой АЧХ уменьшается в раз по сравнению с ее значением на нулевой частоте, то есть

.			(2)
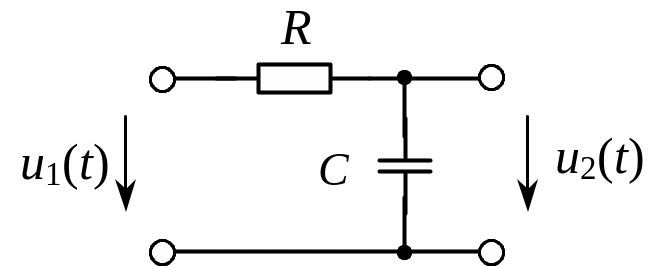
Рис. 1. RC-фильтр нижних частот		Рис. 2. АЧХ реального (а) и идеального (б) ФНЧ

Простейшим ФНЧ является интегрирующая RC-цепь, показанная на рис. 1. АЧХ этой цепи легко найти методом комплексных амплитуд, записав законы Ома и Кирхгофа:

.

(3)

Как видно, k(0) = 1, k() = 0. Сравнение соотношений (2) и (3) позволяет утверждать, что частота среза этого фильтра равна _в = 1/RC. Вид АЧХ (3), а также АЧХ идеального ФНЧ показаны на рис. 2.