
- •Змістовий модуль 1 елементи лінійної алгебри
- •Основні поняття.
- •1.3.1. Основні поняття.
- •Основні поняття.
- •Тема 1.1 Матриці
- •1.1.1 Основні поняття
- •1.1.2. Дії над матрицями
- •Тема 1.2 Визначники
- •1.2.1. Основні поняття
- •1.2.2. Властивості визначників
- •Тема 1.3. Невироджені матриці
- •1.3.1. Основні поняття
- •1.3.2. Обернена матриця
- •1.3.3. Ранг матриці
- •Тема 1.4. Системи лінійних рівнянь.
- •Основні поняття
- •1.4.2 Розв'язок систем лінійних рівнянь. Теорема Кронекера – Капеллі.
- •1.4.3 Розв’язання невироджених лінійних систем. Формули Крамера.
- •1.4.4 Розв'язок систем лінійних рівнянь методом Гауса.
- •1.4.5 Системи лінійних однорідних рівнянь
1.4.3 Розв’язання невироджених лінійних систем. Формули Крамера.
Нехай дана система лінійних рівнянь з невідомими :
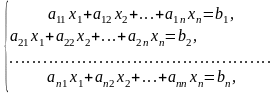 або в
матричній формі
або в
матричній формі
Основна матриця такої системи квадратна. Визначник цієї матриці

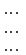
 називається
визначником
системи.
Якщо
визначник системи відмінний від нуля,
то система називається невиродженою.
називається
визначником
системи.
Якщо
визначник системи відмінний від нуля,
то система називається невиродженою.
Знайдемо
розв'язок даної системи рівнянь у випадку
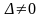 .
Помноживши обидві частини рівняння
зліва на матрицю
,
отримаємо
.
Помноживши обидві частини рівняння
зліва на матрицю
,
отримаємо
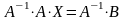 .
Оскільки
.
Оскільки
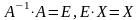 ,
то
,
то
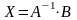 .
(1.4.1)
.
(1.4.1)
Відшукання розв'язку системи за формулою (1.4.1) називається матричним способом розв’язання системи.
Матричну рівність (1.4.1) запишемо у вигляді
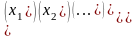 тобто
.
тобто
.
Звідси випливає, що

Але
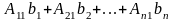 є розклад визначника
є розклад визначника


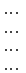
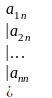 за
елементами першого стовпця. Визначник
за
елементами першого стовпця. Визначник
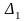 отримується з визначника
шляхом заміни першого стовпця коефіцієнтів
стовпцем з вільних членів.
отримується з визначника
шляхом заміни першого стовпця коефіцієнтів
стовпцем з вільних членів.
Отже,
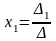 .
.
Аналогічно
:
 ,
де
,
де
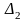 отримується з
шляхом
заміни другого стовпця коефіцієнтами
стовпця з вільних членів;
отримується з
шляхом
заміни другого стовпця коефіцієнтами
стовпця з вільних членів;
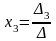 ,…,
,…,
 .
.
Формули
 (1.4.2) називаються формулами
Крамера.
(1.4.2) називаються формулами
Крамера.
Отже, невироджена система лінійних рівнянь з невідомими має єдиний розв'язок, який може бути знайдений матричним способом (1.4.1) або за формулами Крамера (1.4.2)
Приклад 1.4.3. Розв’язати систему
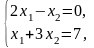
○
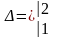
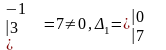
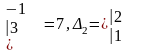
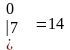 .
Значить
.
Значить
 ●
●
1.4.4 Розв'язок систем лінійних рівнянь методом Гауса.
Один з найбільш універсальних і ефективних методів розв'язку лінійних алгебраїчних систем являється метод Гауса, що за основу має послідовне виключення невідомих.
Нехай дана система рівнянь:
Процес розв'язку за методом Гауса складається з двох етапів. На першому етапі (прямий хід) система приводиться до драбинчастого (зокрема, трикутного) виду.
Наведена нижче система має драбинчастий вигляд:
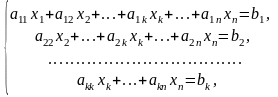 де
де
 .
.
Коефіцієнти
 називаються
головними
елементами системи.
називаються
головними
елементами системи.
На другому етапі (зворотній хід) йде послідовне визначення невідомих з цієї драбинчастої системи.
Опишемо метод Гауса докладніше.
Прямий хід .
Будемо
вважати, що елемент
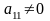 (якщо
(якщо
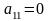 ,
то першим в систему запишемо рівняння,
в якому коефіцієнт при
,
то першим в систему запишемо рівняння,
в якому коефіцієнт при
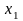 відмінний від нуля).
відмінний від нуля).
Перетворимо
початкову систему, виключивши невідоме
в усіх рівняннях, крім першого
(використовуючи елементарні перетворення
системи). Для цього помножимо обидві
частини першого рівняння на
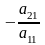 і додамо почленно з другим рівнянням
системи. Потім помножимо обидві частини
першого рівняння на
і додамо почленно з другим рівнянням
системи. Потім помножимо обидві частини
першого рівняння на
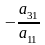 і складемо з третім рівнянням системи.
Продовжуючи цей процес, отримаємо
еквівалентну систему.
і складемо з третім рівнянням системи.
Продовжуючи цей процес, отримаємо
еквівалентну систему.
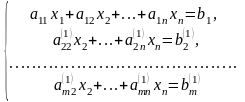
Тут
 - нові значення коефіцієнтів і правих
частин, які отримуються після першого
кроку.
- нові значення коефіцієнтів і правих
частин, які отримуються після першого
кроку.
Аналогічним
чином, вважаючи головним елементом
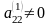 ,
виключимо невідоме
,
виключимо невідоме
 з усіх рівнянь системи, крім першого і
другого, і так далі. Продовжуємо цей
процес допоки можливо.
з усіх рівнянь системи, крім першого і
другого, і так далі. Продовжуємо цей
процес допоки можливо.
Якщо в
процесі приведення даної системи до
драбинчастого вигляду з'являться нульові
рівняння, тобто рівності вигляду 0=0, їх
відкидаємо. Якщо ж з'являться рівняння
вигляду
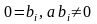 ,
то це свідчить про несумісність системи.
,
то це свідчить про несумісність системи.
Другий
етап (зворотній
хід
) полягає в розв’язку драбинчастої
системи. Драбинчаста система рівнянь,
загалом кажучи, має нескінченну множину
розв’язків. В останньому рівнянні цієї
системи виражаємо перше невідоме
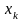 через інші невідомі
через інші невідомі
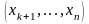 .
Потім підставляємо значення
в передостаннє рівняння системи і
виражаємо
.
Потім підставляємо значення
в передостаннє рівняння системи і
виражаємо
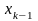 через
;
потім знаходимо
через
;
потім знаходимо
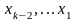 .
Надаючи вільним невідомим
довільних значень, отримаємо нескінченну
множину розв’язків системи.
.
Надаючи вільним невідомим
довільних значень, отримаємо нескінченну
множину розв’язків системи.
Зауваження
1.
Якщо драбинчаста система виявиться
трикутною, тобто
 ,
то початкова система має єдиний розв'язок.
З останнього рівняння знаходимо
,
з передостаннього
,
далі, піднімаючись по системі угору,
знайдемо всі інші невідомі. (
).
,
то початкова система має єдиний розв'язок.
З останнього рівняння знаходимо
,
з передостаннього
,
далі, піднімаючись по системі угору,
знайдемо всі інші невідомі. (
).
2. на практиці зручніше працювати не з системою
,
а з
розширеною її матрицею. Виконуючи всі
елементарні перетворення над її рядками.
Зручно, щоб коефіцієнт
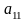 дорівнював 1(рівняння поміняти місцями
або поділити обидві частини рівняння
на
дорівнював 1(рівняння поміняти місцями
або поділити обидві частини рівняння
на
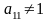 ).
).
Приклад 1.4.4. розв’язати систему методом Гауса:

○ В результаті елементарних перетворень над розширеною матрицею системи
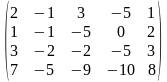 ~
~
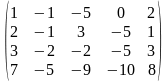 ~
~
~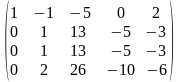 ~
~

Початкова система звелася до драбинчастої
 .
.
Тому
загальний розв'язок системи :
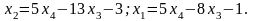 Якщо покласти, наприклад,
Якщо покласти, наприклад,
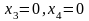 ,
то знайдемо один з частинних розв’язків
цієї системи
,
то знайдемо один з частинних розв’язків
цієї системи
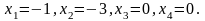 ●
●
Приклад 1.4.5. Розв’язати систему методом Гауса:
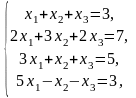
○ Проведемо елементарні перетворення над рядками розширеної матриці системи:
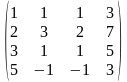 ~
~ ~
~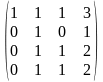 ~
~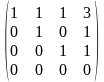
Отримана матриця відповідає системі
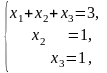
Здійснюючи
зворотній хід, отримуємо
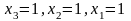 ●
●
