
- •ВВедение
- •Вводное занятие
- •1. Ошибки измерений и их классификация
- •Требования к оформлению отчета
- •Графическое представление результатов
- •Вопросы для самоконтроля:
- •Приборы и принадлежности:
- •Указания мер безопасности
- •Запрещается:
- •Подготовка аппарата к рабоТе
- •Вопросы для самоконтроля:
- •Приборы и принадлежности:
- •Лабораторная работа
- •Устройство и принцип работы установки
- •Вопросы для самоконтроля
- •Приборы и принадлежности:
- •Вопросы для самоконтроля:
- •Приборы и принадлежности:
- •Лабораторная работа
- •Вопросы для самоконтроля:
- •Приборы и принадлежности:
- •Семинар №1
- •План изучения темы:
- •Литература:
- •Вопросы для самоконтроля:
- •Семинар №2
- •План изучения темы:
- •Литература:
- •Семинар № 3
- •План изучения темы:
- •Литература:
- •Семинар №4
- •План изучения темы:
- •Литература:
- •Лабораторная работа
- •Цель занятия:
- •Литература:
- •Лабораторная работа
- •Устройство и принцип действия аппарата «амплипульс-5»
- •Подготовка аппарата «Амплипульс – 5» к работе
- •Вопросы для самоконтроля:
- •Лабораторная работа
- •Цель занятия:
- •Теоретические предпосылки работы
- •Меры безопасности:
- •Вопросы для самоконтроля
- •Лабораторная работа
- •Теоретические предпосылки работы
- •Вопросы для самоконтроля
- •Описание установки
- •Вопросы для самоконтроля:
- •Семинар 7
- •План изучения темы: литератуРа:
- •Семинар 8
- •План изучения темы: литератуРа:
- •Семинар 9
- •План изучения темы: литератуРа:
- •Семинар 10
- •План изучения темы: литератуРа:
- •Семинар 11
- •План изучения темы: литератуРа:
- •Дозиметрия ионизирующего излечения план изучения темы: литератуРа:
- •Семинар 13
- •План изучения темы: литератуРа:
- •Экзаменационные вопросы
Вопросы для самоконтроля:
1. Что называется внутренним трением или вязкостью жидкости?
2. Каковы причины и как проявляется внутреннее трение?
3. От чего зависит сила внутреннего трения (формула Ньютона)?
4. Что такое коэффициент внутреннего трения, в чем его смысл, единицы измерения?
5. Что такое ньютоновские и неньютоновские жидкости?
6. Относится или нет кровь к ньютоновским жидкостям? Почему?
7. Какое течение жидкости называется ламинарным, турбулентным?
8. Каково условие ламинарного течения жидкости?
9. Что определяется числом Рейнольдса?
9. Что представляет собой формула Пуазейля? Справедлива ли она в случае турбулентного течения жидкости?
10. Методы определения вязкости. Как устроен медицинский вискозиметр?
11. Какова последовательность действий при определении коэффициента вязкости медицинским вискозиметром?
Приборы и принадлежности:
Установка для определения коэффициента вязкости методом Пуазейля, исследуемые жидкости, дистиллированная вода, капиллярная трубка, секундомер.
Схема работы:
Последовате-льность действий |
Способ выполнения задания |
|||||
1.Исследование зависимости коэффициента вязкости раствора от его концентрации |
1. Залейте в бюретку 20-25 мл дистиллированной воды. 2. Опустите капилляр на 1-2 мм в жидкость, находящуюся в сосуде под бюреткой. Измерьте время истечения 20 мл воды (от отметки 0 до отметки 20мл) из капилляра. Измерения проведите 3 раза, сохраняя постоянными верхний и нижний уровни жидкости в бюретке. 3. Проведите аналогичные измерения с растворами с плотностями ρ1, ρ2 и ρ3. 5. Результаты измерений занесите в таблицу 1 (см. ниже).
Таблица 1 |
|||||
Наименование жидкости |
№ |
t (c) |
η (Па·с) |
ηср (Па·с) |
|
|
Дистиллированная вода |
1 |
|
- |
0,001 |
|
|
2 |
|
- |
||||
3 |
|
- |
||||
Раствор №1 |
1 |
|
|
|
|
|
2 |
|
|
||||
3 |
|
|
||||
Раствор №2 |
1 |
|
|
|
|
|
2 |
|
|
||||
3 |
|
|
||||
Раствор №3 |
1 |
|
|
|
|
|
2 |
|
|
||||
3 |
|
|
||||
2. Обработка результатов измерений |
1. По формуле (3) рассчитайте коэффициенты вязкости и вычислите ηср для каждого из растворов. 2. Результаты занесите в таблицу 1. 3. Полученную зависимость изобразите графически: η = f(ρ). 4. Проанализируйте полученные результаты и сформулируйте выводы. 5. Рассчитайте относительную погрешность в каждом эксперименте. Результаты занесите в таблицу. Если ошибка не превышает 10%, метод можно считать освоенным. Примечание: плотность воды ρН2О=1000 Кг/м3; плотности растворов ρ1=1022 Кг/м3, ρ2=1045 Кг/м3, ρ3=1067 Кг/м3.
|
|||||
Лабораторная работа
Изучение механических моделей биологических тканей
Во многих разделах и направлениях медицины (космическая медицина, спортивная медицина, судебная медицина, ортопедия и др.) врачу важно иметь представление о пассивных механических свойствах биологических тканей.
ЦЕЛЬ занятия:
1. Исследование поведения различных моделей тканей при различных режимах деформации.
ИСХОДНЫе ЗНАНИя:
1. Знать виды механических деформаций.
ПЛАН ИЗУЧЕНИЯ ТЕМЫ:
1. Деформация.
2. Виды деформаций.
3. Механические модели тел.
4. Механические свойства биологических тканей.
ЛИТЕРАТУРА:
1. Лекции.
2. А.Н. Ремизов. Медицинская и биологическая физика, М., 2004, гл. 8, с. 139 - 150.
3. М.Е. Блохина, И.А. Эссаулова, Г.В. Мансурова. Руководство к лаб. работам по медицинской и биологической физике, М., 2001, с. 89—96.
ТЕОРЕТИЧЕСКИЕ ПРЕДПОСЫЛКИ РАБОТЫ
Изучению механических свойств биологических тканей в биофизических исследованиях уделяют большое внимание. Исследования взаимосвязи структуры тканей и их механических свойств, особенностей поведения тканей при различных режимах нагрузки позволяют решать конкретные медицинские задачи: разработку материалов для замещения пораженных тканей; оценку механических параметров биологических тканей в норме и при патологии с целью диагностики и др.
Механические свойства твердых тел проявляются при деформациях. Кроме упругой и пластической деформаций, различают также другие виды деформаций.
Упругопластической называется деформация, которая частично сохраняется после прекращения действия внешней силы.
Вязкоупругой называется деформация, которая при действии постоянной силы с течением времени достигает значительной величины, а после снятия нагрузки постепенно исчезает полностью или частично. Этот вид деформации наиболее характерен для полимеров и обусловлен строением их молекул. Для вязкоупругих объектов характерны явления ползучести и релаксации напряжения.
Ползучесть — явление изменения относительной деформации объекта с течением времени при постоянном напряжении: ε = f(t) при σ = const. Процессы, происходящие в полимерах при ползучести, соответствуют течению вязкой жидкости. Исследование ползучести проводят в изотоническом режиме Деформации: в объекте создают постоянное механическое напряжение σ = const (действуют постоянной силой) и изучают зависимость ε = f(t).
Релаксация напряжения — уменьшение механического наряжения с течением времени при постоянной величине относительной деформации: σ = f(t) при ε = const.

Рис. 1.
Исследование релаксации напряжения проводят в изометрическом режиме деформации: в объекте создают ступенчатое удлинение и, сохраняя его постоянным (ε = const), изучают зависимость σ = f(t).
При изучении механических свойств любого материала исследуют, прежде всего, зависимость механического напряжения от относительной деформации ε: σ = f(ε) и временные зависимости напряжения σ = f(t) и относительной деформации ε = f(t).
Биологические ткани такие, как мышцы, сухожилия, кровеносные сосуды, костная ткань, представляют собой вязкоупругие системы. Их пассивные механические свойства, проявляющиеся под действием внешней силы, удобно моделировать сочетанием упругих и вязких элементов.
Модель упругого элемента — идеально упругая пружина (рис. 1, а), в которой процесс деформации происходит мгновенно и подчиняется закону Гука:
σ = Е·ε, (1)
где Е- модуль упругости. На рисунке 1, б изображен график зависимости σ = f(ε); а на рисунке 1, в и г — графики зависимости ε = f(t) в изотоническом и σ = f(t).в изометрическом режимах.
Модель вязкого элемента — поршень с отверстиями, движущийся в цилиндре с вязкой жидкостью (рис. 2, а). При движении поршня жидкость протекает через отверстия и создает сопротивление, которое растет пропорционально скорости движения поршня. Относительная деформация вязкого элемента пропорциональна времени t действия внешней силы и зависит от напряжения σ и вязкости η жидкости:
![]() (2)
(2)
На рисунке 2, б, в
изображены графики зависимости σ
= f
![]() и ε = f(t)
в изотоническом режиме.
и ε = f(t)
в изотоническом режиме.

Рис. 2.
Исследование реформации вязкого элемента в изометрическом режиме невозможно, так как нельзя ступенчато изменить относительную деформацию (мгновенно вытянуть поршень).
Вязкоупругие свойства тел моделируются системами, состоящими из различных комбинаций моделей упругого и вязкого элементов.
Модель Кельвина - Фойгта — параллельное соединение упругого и вязкого элементов (рис. 3, а).

Рис. 3.
При постоянно действующей силе относительная деформация этой модели экспоненциально возрастает со временем. После снятия нагрузки деформация экспоненциально убывает, и через некоторое время система возвращается в исходное состояние (ε = 0) [см. кривую ползучести, приведенную на рис. 3, б].
Модель Максвелла – последовательное соединение упругого и вязкого элементов (рис. 4, а). σ
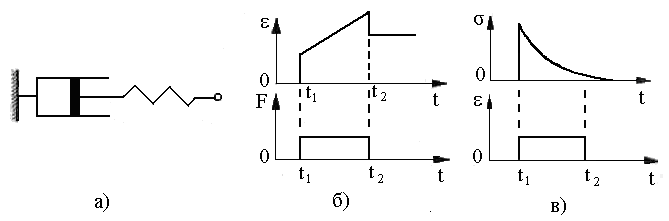
Рис. 4.
В изотоническом режиме (рис. 4, б) пружина мгновенно удлиняется (момент времени t1) до значения, определяемого законом Гука, а поршень движется с постоянной скоростью до тех пор, пока действует постоянная внешняя сила. После снятия нагрузки (момент времени t2) пружина мгновенно сокращается, а положение поршня остается неизменным. В изометрическом режиме (рис. 4, в) пружина после быстрого растяжения начинает сокращаться, вытягивая при этом поршень, т. е. происходит релаксация напряжения.
Модель Зинера — последовательное соединение моделей Кельвина — Фойгта и упругого элемента (рис. 5, а).
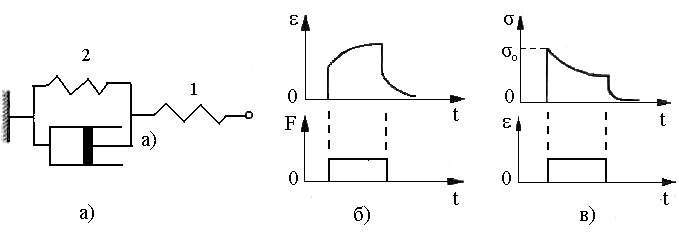
Рис. 5.
В изотоническом режиме (рис. 5, б) пружина 1 мгновенно удлиняется до значения, определяемого законом Гука, а пружина 2 удлиняется постепенно по мере вытягивания поршня и ее удлинение имеет нелинейный характер. После прекращения действия внешней постоянной силы пружина мгновенно сокращается, пружина 2 сокращается постепенно, втягивая поршень в обратном направлении. Таким образом, после снятия нагрузки в модели не сохраняется остаточная деформация. Зависимость деформации от времени имеет сложный характер: она определяется начальным напряжением, модулями упругости пружин 1 и 2 и вязкостью системы. В изометрическом режиме (рис. 5, в) в пружине 1 мгновенно создается напряжение σ0, затем напряжение убывает по экспоненциальному закону, так как происходит постепенное вытягивание поршня и растяжение пружины 2. После прекращения деформации напряжение резко падает до некоторой величины (сокращается пружина 1), а затем плавно убывает до нуля.
Механические свойства биологических тканей обусловлены их строением.
Мышцы. В состав мышц входят волокна коллагена и эластина, поэтому они ведут себя подобно полимерам — в них происходит вязкоупругая деформация. Гладкие мышцы при деформации ведут себя подобно модели Максвелла (см. рис. 3). Для них характерна релаксация напряжения, поэтому они могут сильно растягиваться без особого напряжения, что способствует большей растяжимости полых органов. Скелетные мышцы при деформации подобны модели Зинера (см. рис. 5): при быстром растяжении напряжение в них быстро возрастает, а затем постепенно уменьшается до некоторого остаточного значения. В отличие от модели зависимость σ = f(ε) для скелетной мышцы нелинейная.
Кости. Костная ткань по своим свойствам отличается от мышц. По своему поведению при деформации костная ткань подобна модели Зинера (см. рис. 5). Минеральные компоненты костной ткани обеспечивают ее упругие свойства и быструю деформацию, а органические волокна коллагена — вязкие свойства и определяют ползучесть кости.
Вопросы для самоконтроля:
1. Дайте определение механической деформации.
2. Перечислите возможные виды деформаций.
3. В чем заключаются изотонический и изометрические режимы деформации?
4. Что называется релаксацией напряжения и ползучестью?
5. Укажите модели твердых тел: упругого элемента, вязкого элемента, Максвелла, Кельвина - Фойгта, 3инера и опишите особенности их деформаций.
6. Опишите механические свойства биологических тканей.
Приборы и принадлежности:
Персональный компьютер.
Схема работы
Последовательность действий |
Способ выполнения задания |
1. Исследование поведения механических систем при воздействии нагрузкой. |
1. Выберите в окне первую модель (модель упругого элемента). Выберите скорость движения графика. Подведите курсор мыши к метке «0,1» и нажмите левую клавишу мыши. Получите четыре изолнии. 2. Дайте нагрузку: установите курсор мыши на кнопку «PUSH», нажмите левую клавишу мыши и держите ее. 3. Снимите нагрузку: отпустите левую клавишу. действия, аналогичные п. 1.-3., для остальных моделей. 4. Остановите график: подведите курсор мыши к отметке «STOP» и нажмите левую клавишу мыши 5. Зарисуйте в тетрадь все полученные графики (зависимость относительного удлинения от времени и напряжения от времени при действии внешней нагрузки и после снятия нагрузки). 6. Сделайте вывод о поведении элемента при заданных режимах деформации. 7. Проделайте действия, аналогичные п. 1 - 6, для остальных моделей. |
2. Выполнение контрольных заданий. |
1. Определите модуль упругости ахиллова сухожилия. Ответы занесите в тетрадь. 2. Выполните задания по предложенным моделям. Ответы занесите в тетрадь.
|
