1. Дифференциальные уравнения с разделяющимися переменными

Дифференциальное уравнение называется уравнением с разделяющимися переменными, если имеет следующий вид:

y′=f₁(x)∙f₂(y) (1)

Предположим, что . Тогда уравнение можно записать так:

(2)

Уравнение (2) называется уравнением с разделенными переменными.

Интегрируя почленно уравнение (2), получим общее решение уравнения (1)

.

Алгоритм решения

1) Разделить переменные (с учетом условий, когда это можно сделать).

2) Интегрировать почленно полученное уравнение.

3) Выяснить, имеет ли уравнение решение, не получившего из общего интеграла.

4) Найти частное решение (если нужно).

2. Однородные ду первого порядка

  Определение.  Функция f(x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:

 Например, функция  является однородной третьего порядка, т.к.

   Определение. Уравнение вида P(x, y)dx+Q(x, y)dy=0, (3)

где P(x, y), Q(x, y) – однородные функции x и y одинаковой степени, называется однородным дифференциальным уравнением.

Уравнение (3) можно привести к виду (4)

  Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными с помощью подстановки

, т.е. y=ux  и y^/=u^/x+u

После решения полученного ДУ относительно u, нужно выразить u через x и у и решить новое ДУ с разделяющимися переменными.

3. Линейные ду первого порядка

  Определение. Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:

(4)

при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением. 

  Рассмотрим методы нахождения общего решения линейного однородного дифференциального уравнения первого порядка вида

(5)

 Такого типа дифференциальные уравнения можно свести к уравнениям с разделенными переменными.

,

     Для интегрирования линейных неоднородных уравнений (Q(x)0) применяется основном метод Бернулли.   Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций  y=uv, где u=u(x), v=v(x)—некоторые функции от x, тогда y^/=u^/v+uv^/. Этот метод более подробно рассмотрен в практической части.

 

  Практическая часть

Пример 1. Решить дифференциальное уравнение: y′tgx=1+y, если при ;

Решение. Уравнение является дифференциальным уравнением с разделяющимися переменными, где f₁(x)=tgx, f₂(y)=1+y.

ln|1+y|=ln|sinx|+C_1,

1+y=sin x ,

y=Csin x-1.

Находим С, подставляя в данное равенство начальные данные условия.

С=1.

Таким образом,

y=sin x-1.

Ответ: y=sin x-1.

Пример 2. Решить уравнение .

Решение. Заданное уравнение имеет вид (3), т.е. является однородным диф. уравнением первого порядка. Приведем его к виду (4):

Пусть тогда и уравнение привет вид:

т.к. то

-- общее решение заданного уравнения.

Ответ: _.

Пример 3. Решить уравнение (x²-2y²)+2xy =0

Решение. (x²-2y²)+2xy =0.

(x²-2y²)dx+2xydy=0.

В данном уравнении функции P(x, y)=x²-2y², Q(x, y)=2xy – однородные второго измерения, следовательно, данное уравнение является однородным дифференциальным уравнением первого порядка.

Положим, у=ux, откуда:

dy= udx+x du.

Уравнение примет вид:

x²dx-2(zx)²dx+2x ux(u dx+x du)=0,

x²dx-2u²x²dx+2u²x²dx+2ux³du=0,

dx+2uxdu=0,

,

, ,

Учитывая, что u=y/x, находим общий интеграл

Ответ:

  Пример 4.  Найти общее решение уравнения

Решение. Данное уравнение имеет вид (4), т.е. является линейным уравнением. Пусть

y=uv, y^/=u^/v+uv^/. Тогда уравнение примет вид:

(6)

Подберем функцию так, чтобы выражение в скобках было равно нулю, т.е.

,

,

Интегрируя равенство, получим

,

.

Подставим полученное решение в (6).

.

Итак, общее решение .

Ответ:

 

Практические задания

1-2-- Найти общее решение ДУ с разделяющимися переменными.

3-- Найти частное решение ДУ с разделяющимися переменными.

4--Найти общее решение однородного ДУ первого порядка.

5-- Найти общее решение линейного ДУ первого порядка.

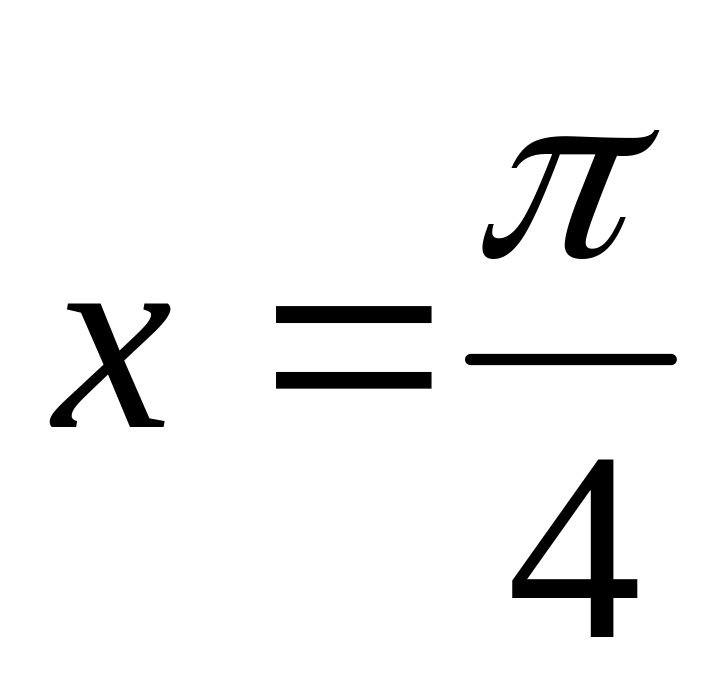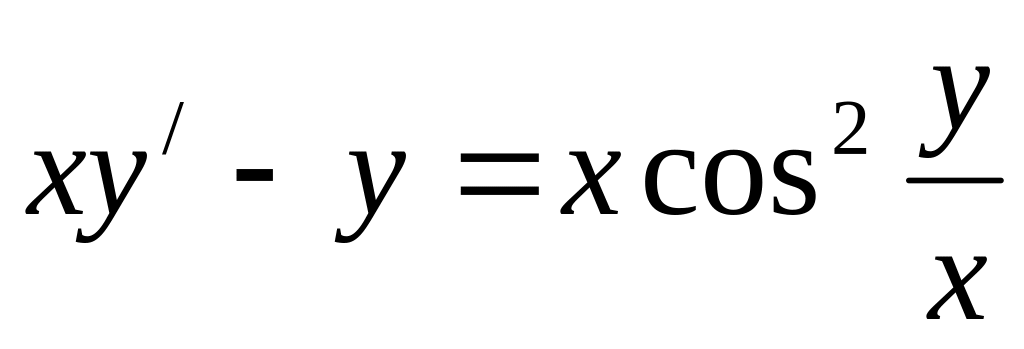
1 вариант ydy=x3dx. xydy=(y2-1)dx ydx+ctg xdy=0, если у=1 при . y/+2xy=2xy3	2 вариант 4y2dx=x2dy. x2dx=ydy. (1+x)ydx=(y-1)xdy, если у=1 прих=1. ydx+(x+y)dy=0. y/+ycosx=sin2x
3 вариант x3dx=(y-1)dy. (x+3)dy=(y-1)dx. x2dy-y2dx=0, если у=1 при х=0,2.	4 вариант 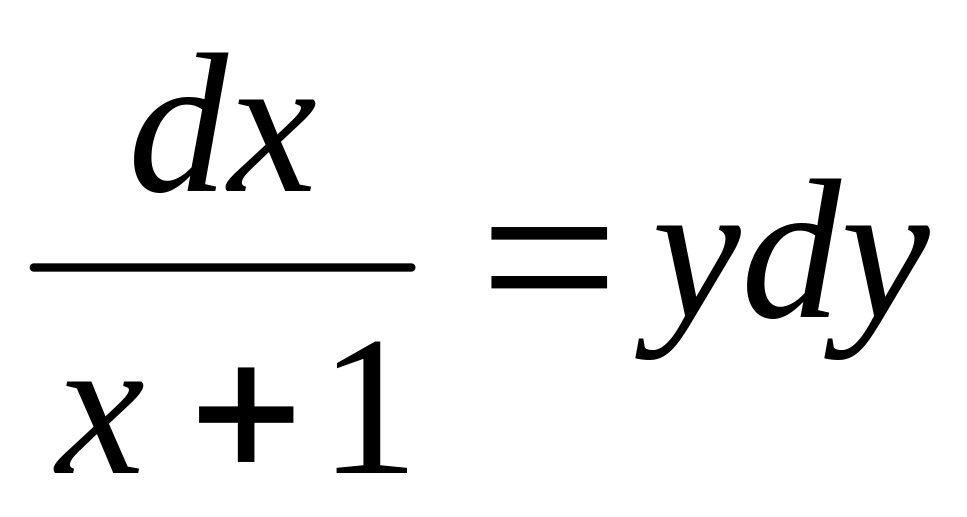. dy+y tg xdx=0. x2dy- 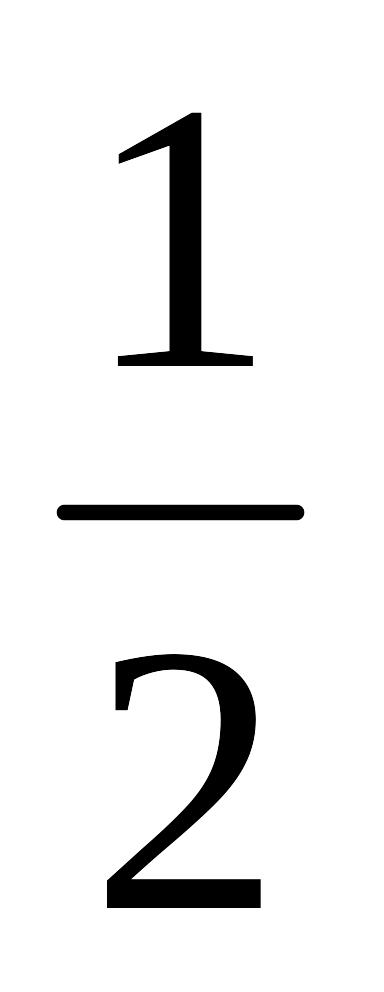y3dx=0, если у=1 при х=-1. . .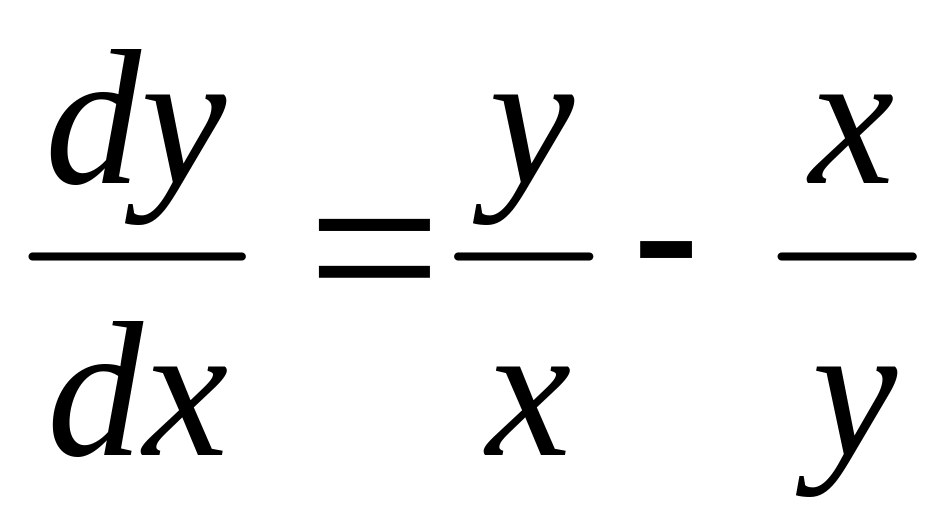
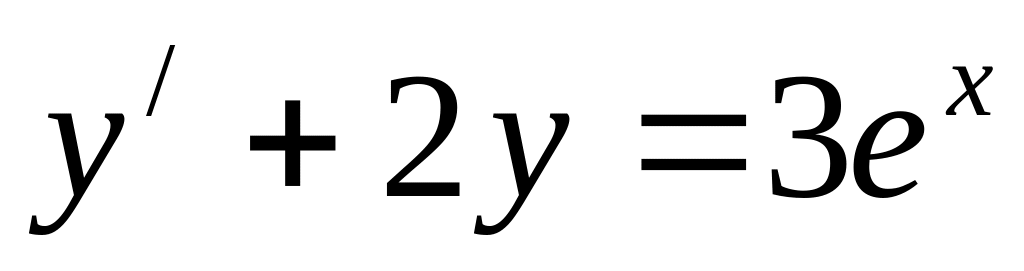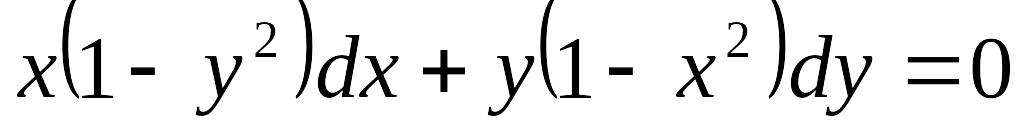
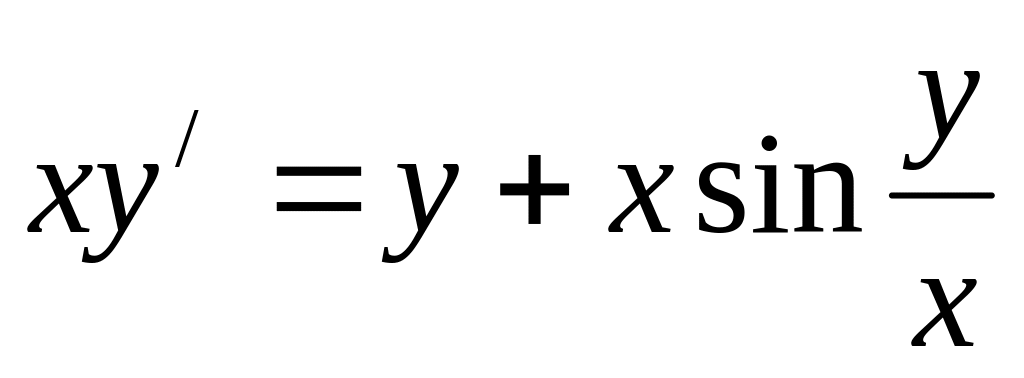
Вариант 5 xdy=ydx y/=sin5x, y(π/2)=1 y/+y=e-x	Вариант 6 xdy=y4dx xyy/=1-x y/=6 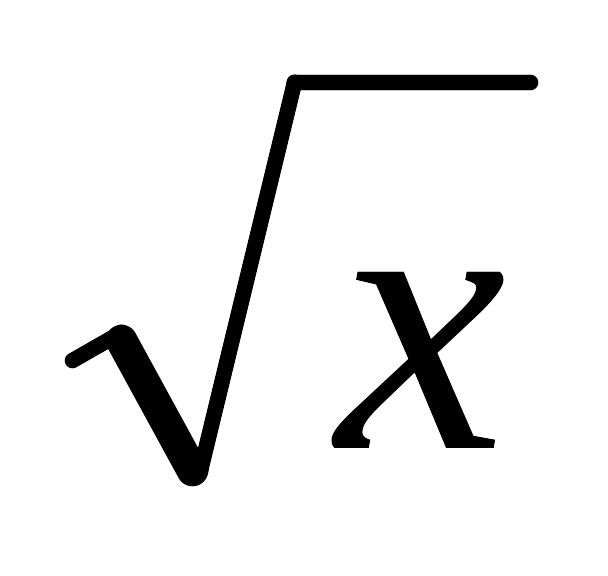dx yy/-2y+x=0 xy/+y=sinx
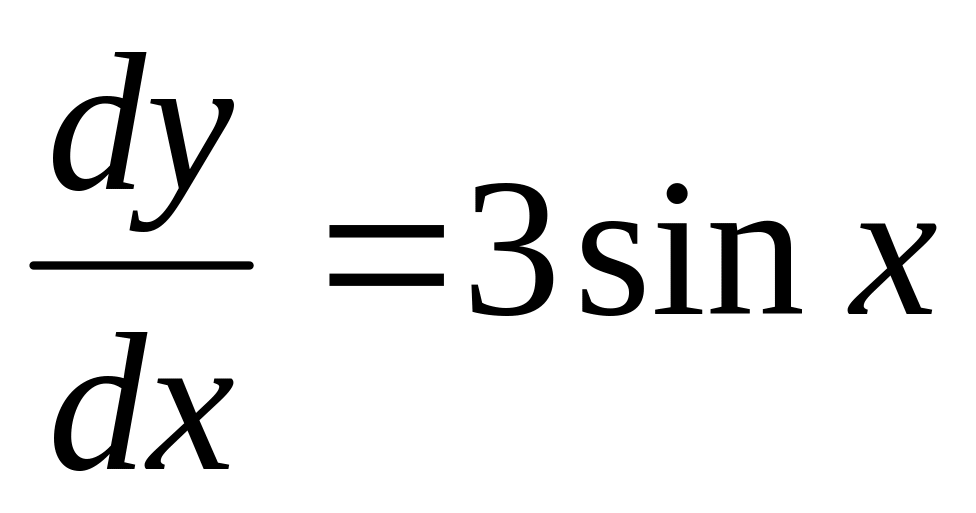
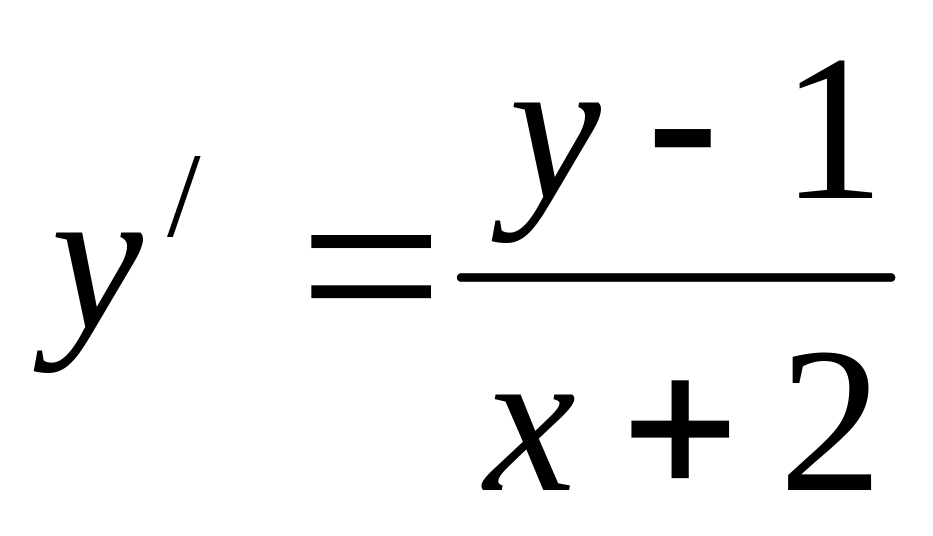
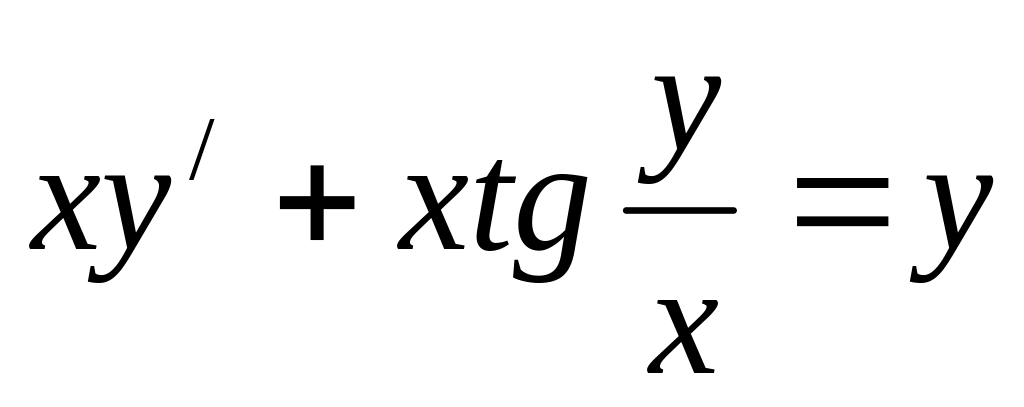
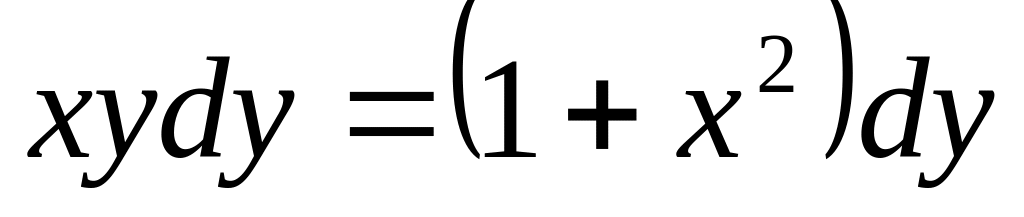
Вариант 7 x2dy-dx, y(1)=2 y/+2xy=2x3	Вариант 8 (2-y)dy=xdx 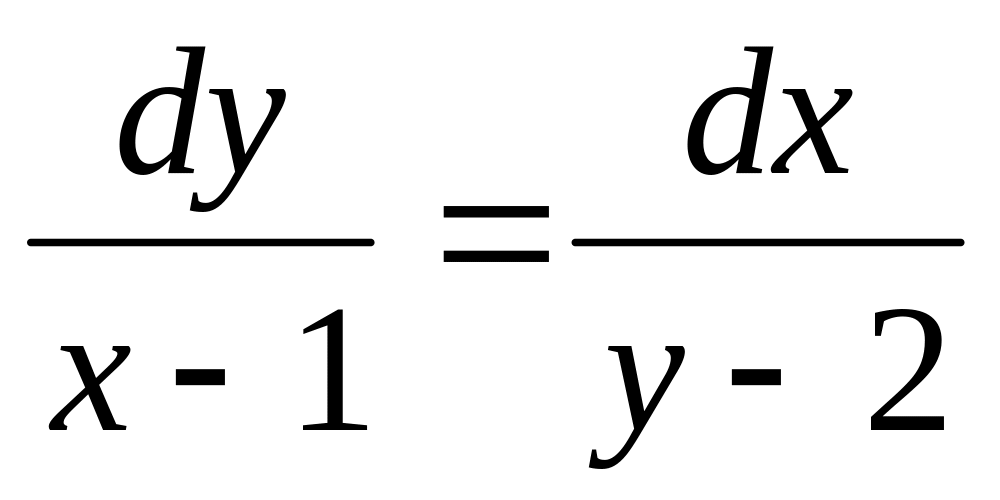, если у=4 при х=0 (3x2-y2)y/=2xy xy/+y=x+1
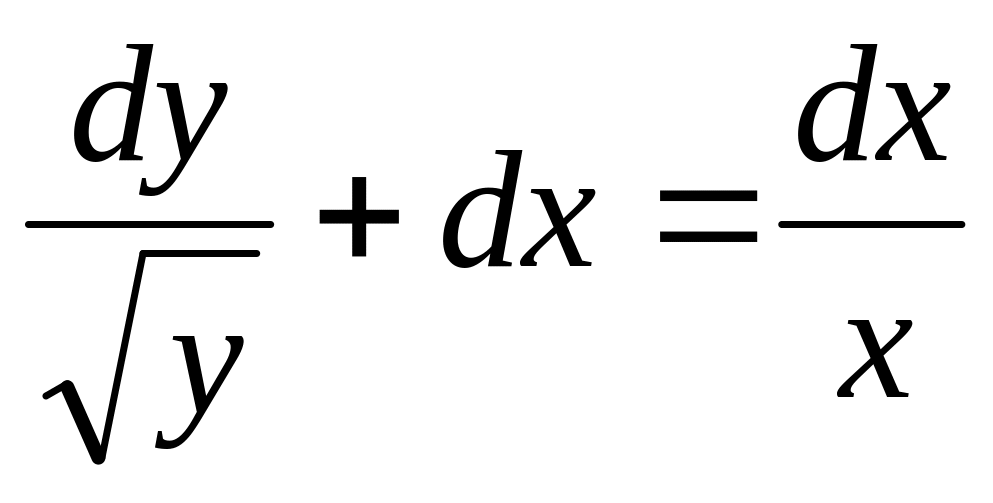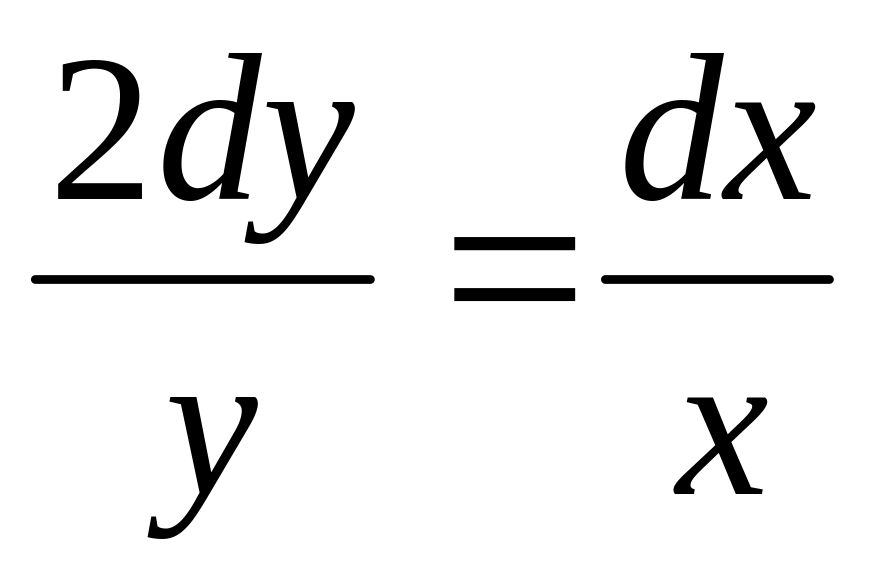
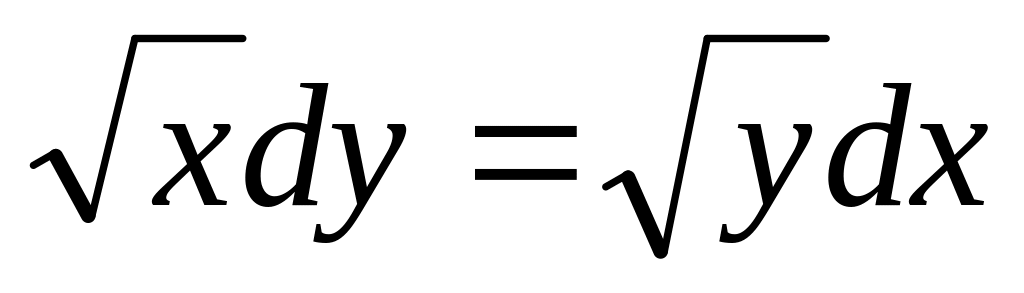
Вариант 9 y/-3xy=0 xdy+y3dx=0 , если у=1 при х=1. 2xyy/=x2+y2 y/-ysinx=sinxcosx	Вариант 10 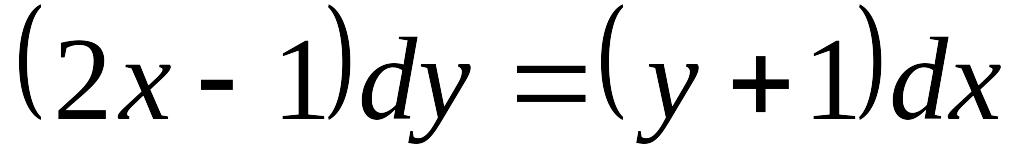, если у=0 при х=1 x2y/=y2-xy+x2
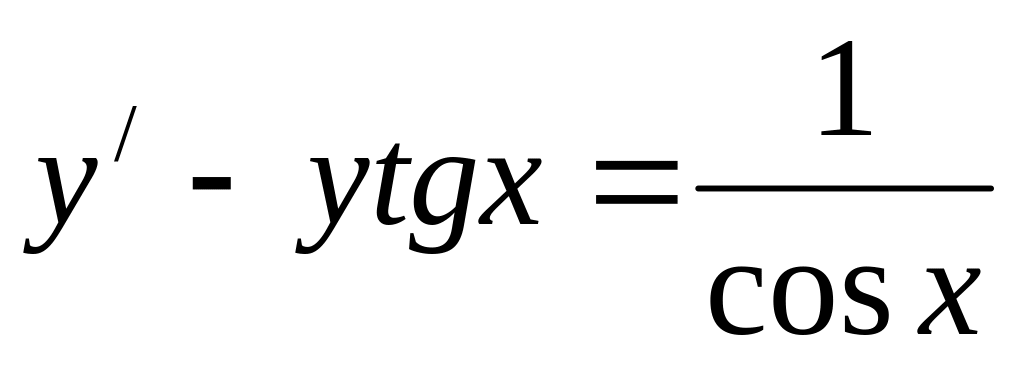
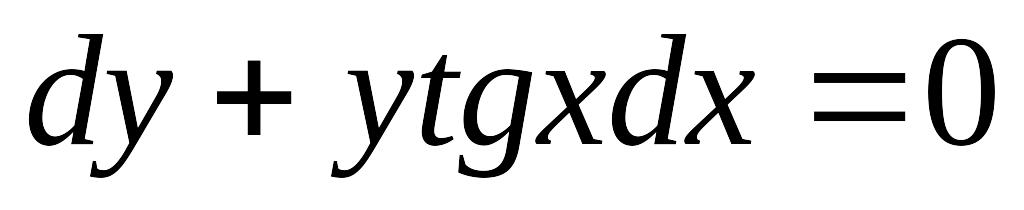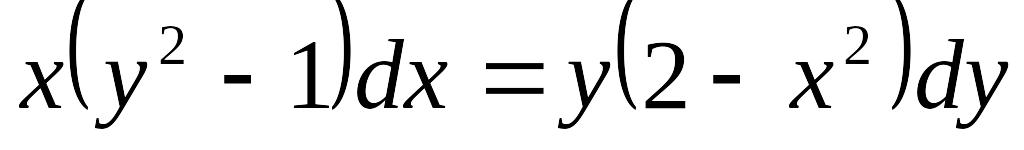
Вариант 11 ydy=exdx , если у=1 при х=0. (x-y)ydy-x2dy=0 xy/+y=3	Вариант 12 x3dx=(3-y)dy y2dx=exdy, если у=1 при х=0. xy2y/=x3+y3 xy/-3y=x4ex
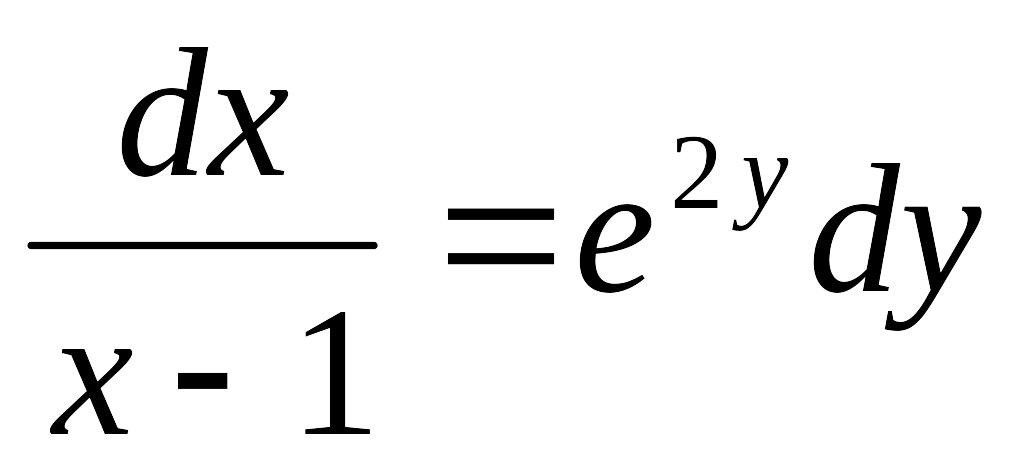
Вариант 13 xydх-(2+x2)dy=0. 1+y2=xyy/, y(2)=1 x3dy-y(x2+y2)dx=0. xy/-y-x3=0	Вариант 14 y/+y=5 x2dy+(y-3)dx=0 cosxsinydy=cosysinxdx, y(π)=π. x2y/=xy+y2 y/-3xy=2xy2

Контрольные вопросы:

1. Что называется дифференциальным уравнением?

2. Как определить порядок диф. уравнения?

3. Что называется общим решением диф. уравнения? Частным?

4. Диф. Уравнения с разделяющимися переменными. Алгоритм их решения.

5. Однородные диф. уравнения первого порядка. Алгоритм их решения.

6. Линейные диф. уравнения первого порядка. Алгоритм их решения (Метод Бернулли).