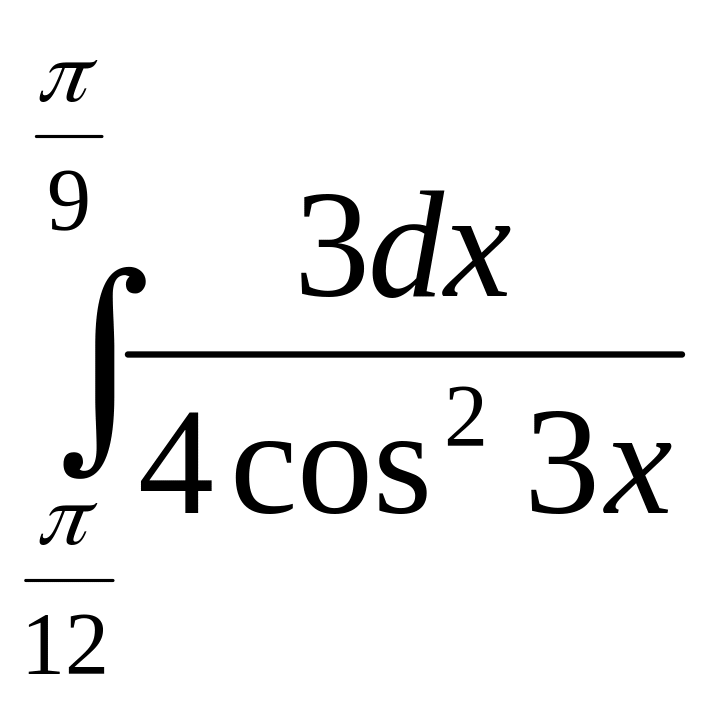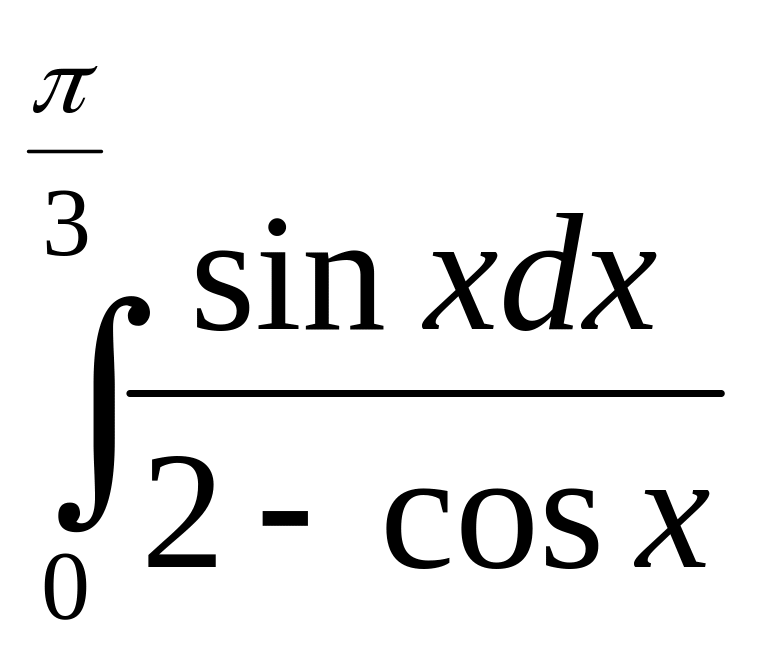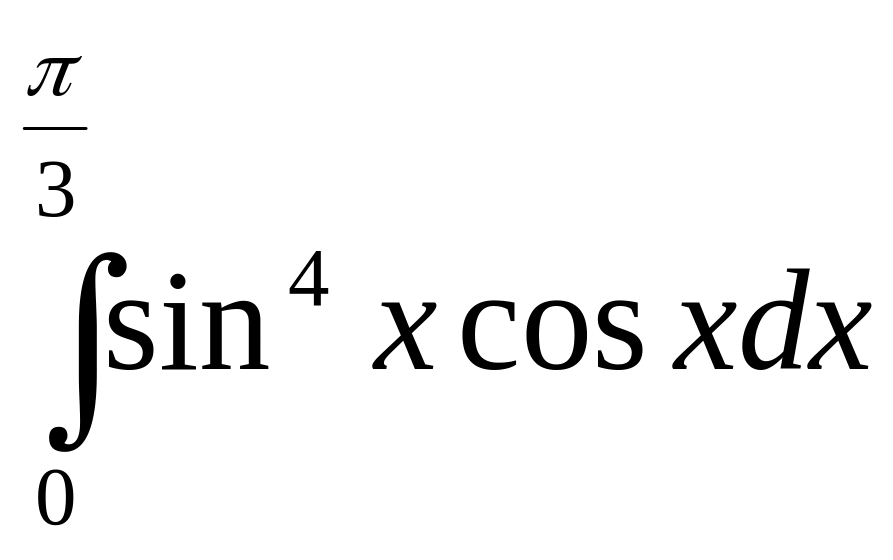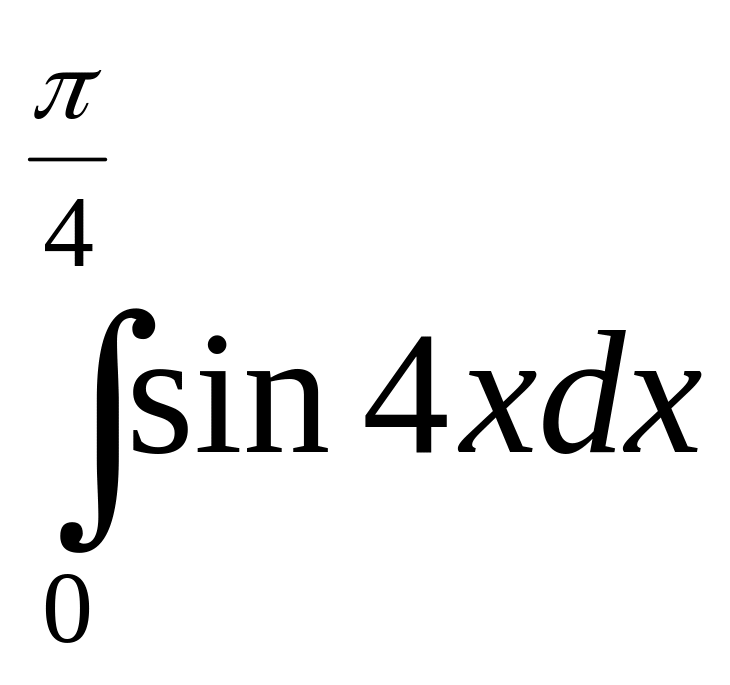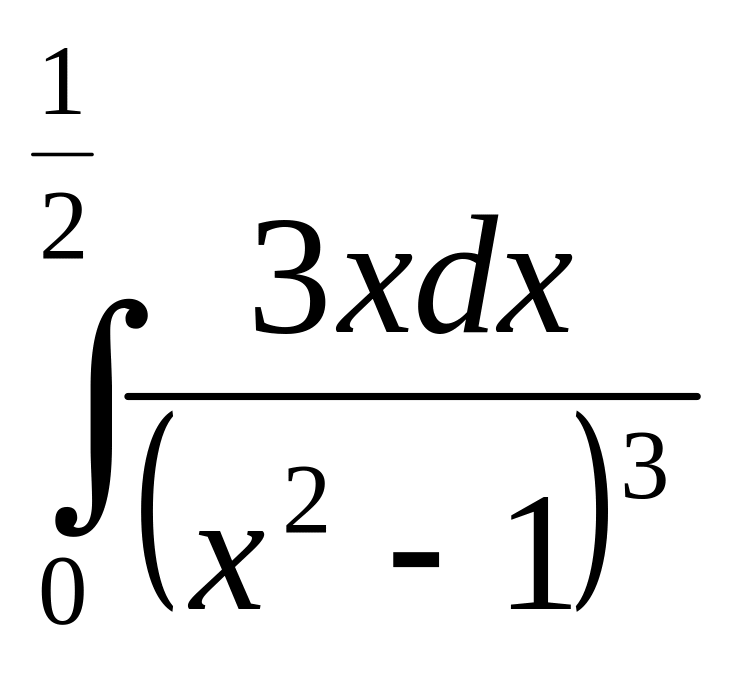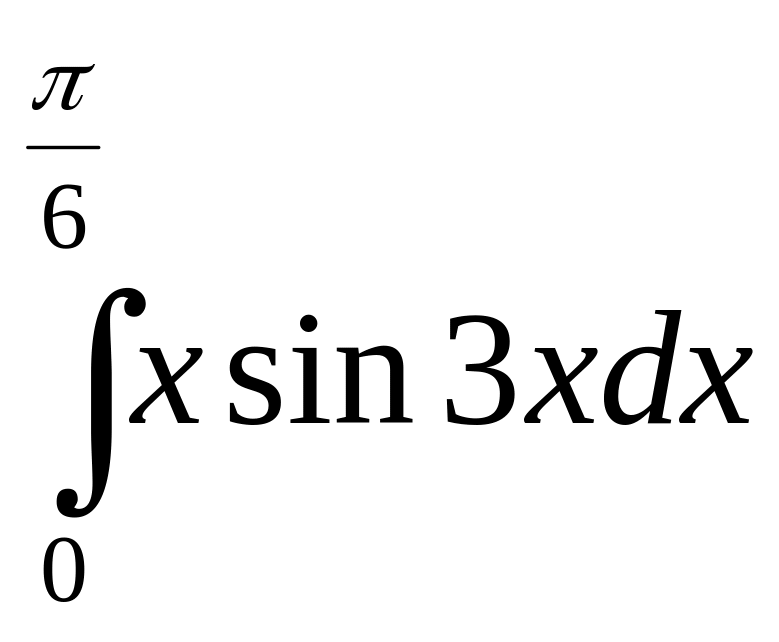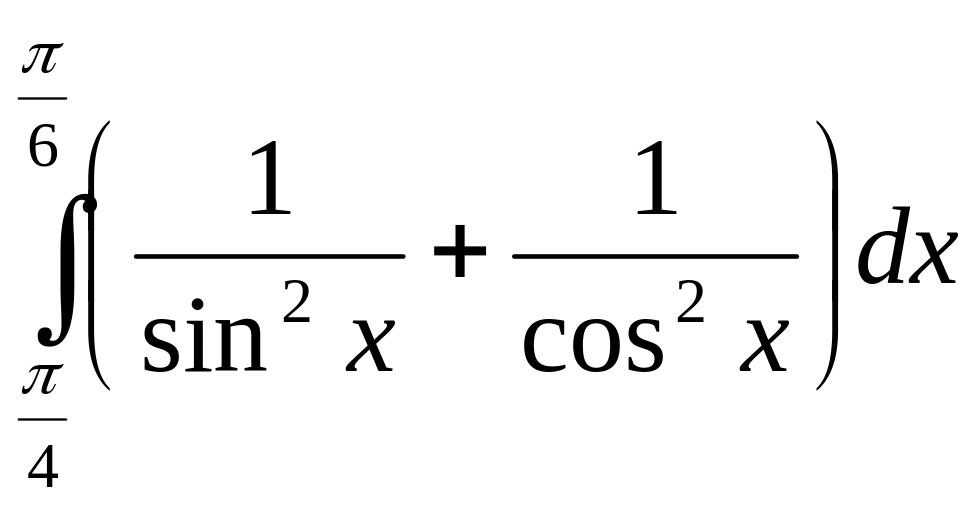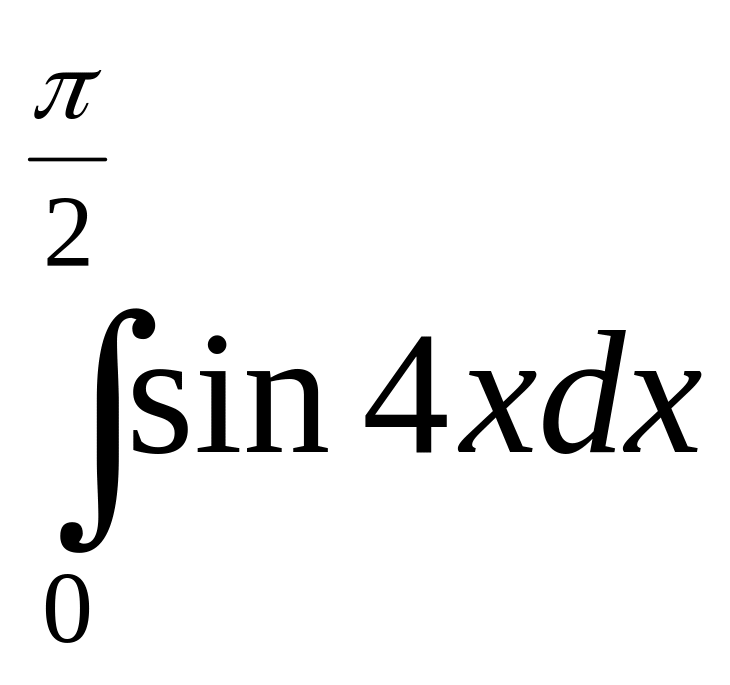- •Практические задания
- •Практические задания
- •Вычисление площадей плоских фигур с помощью определенного интеграла
- •Объем тел вращения.
- •Вычисление пути, пройденного точкой
- •Работа переменной силы
- •1. Дифференциальные уравнения с разделяющимися переменными
- •2. Однородные ду первого порядка
- •3. Линейные ду первого порядка
- •Пояснительная записка
Практические задания
Построить графики функции:
y=x ln x. 8)
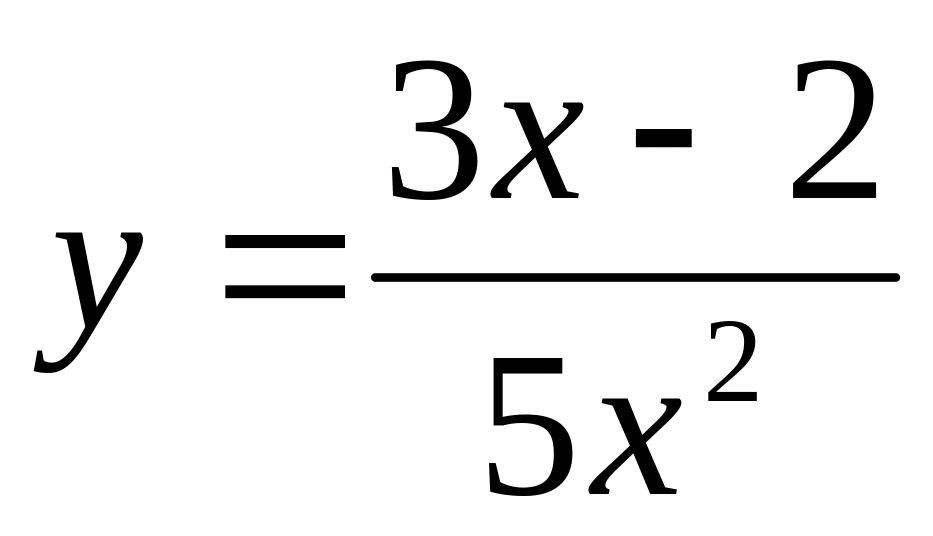
y=(x-1)ex. 9)
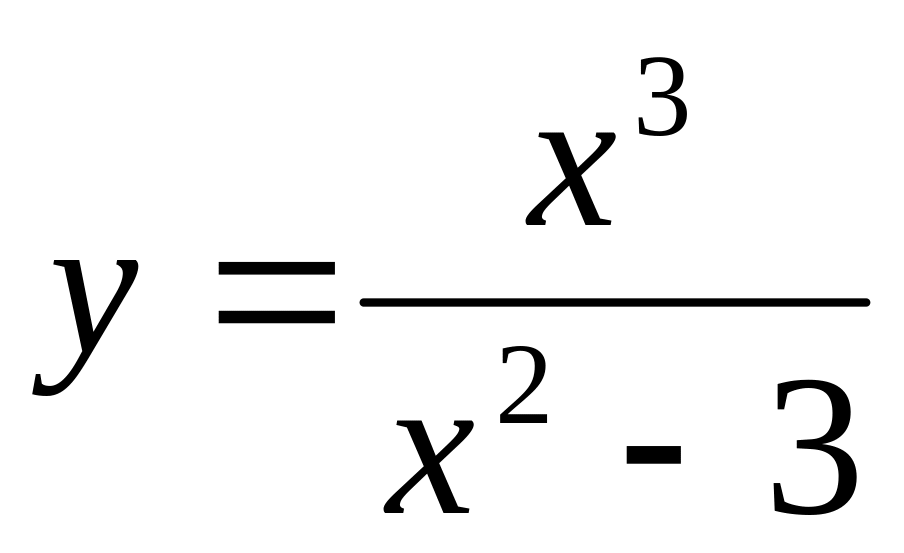
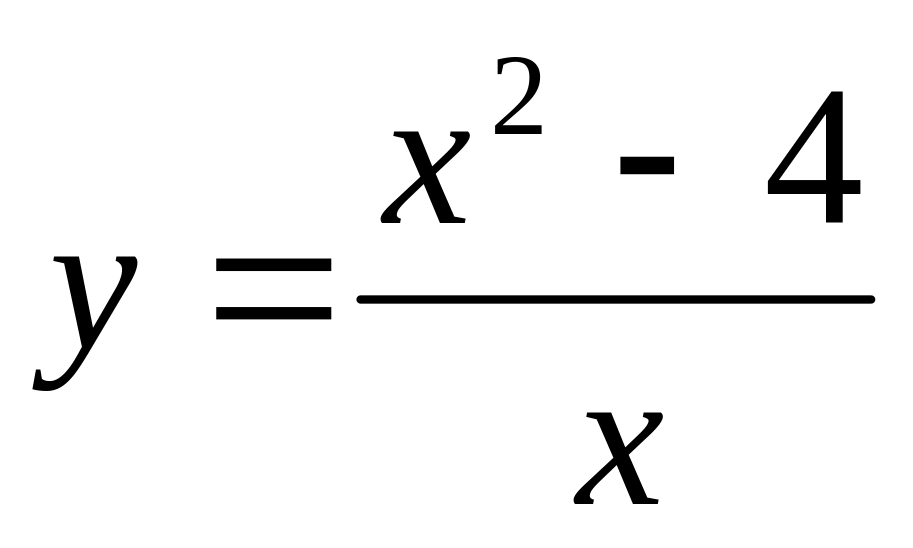 10)
10)

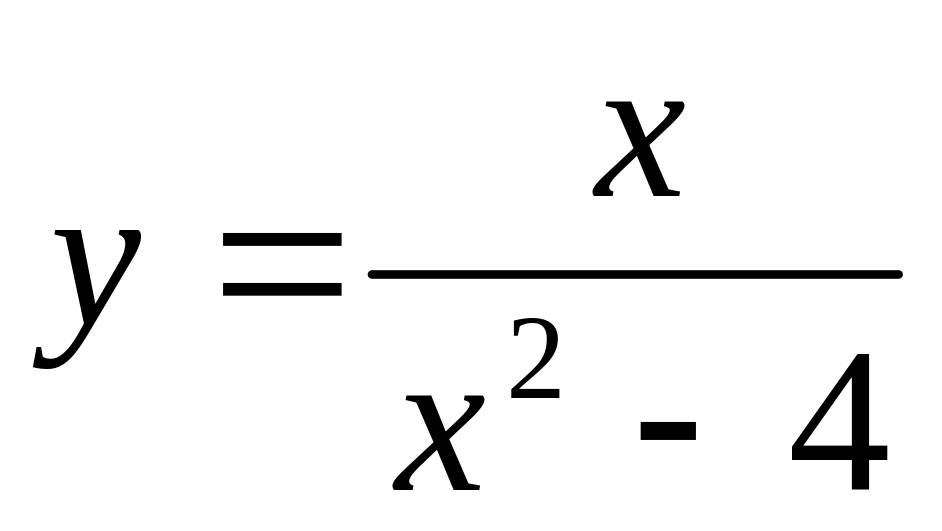 11)
11)
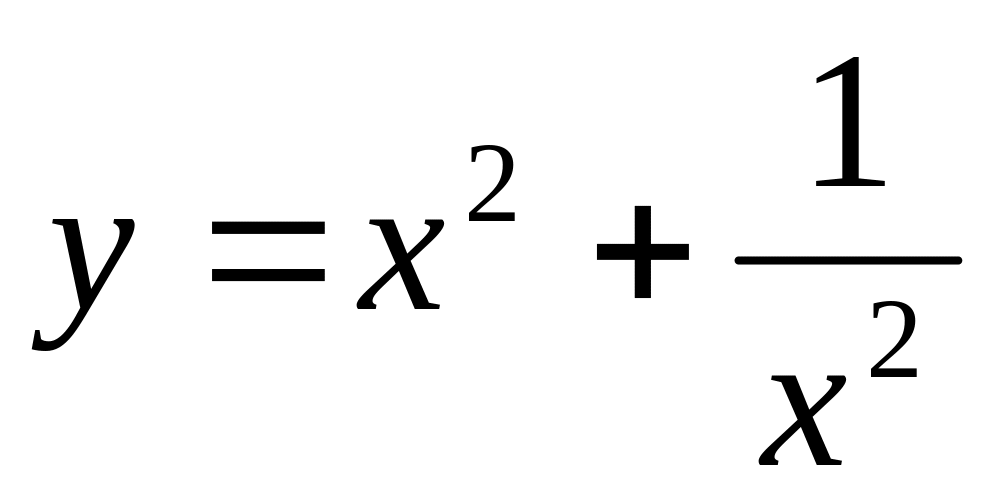
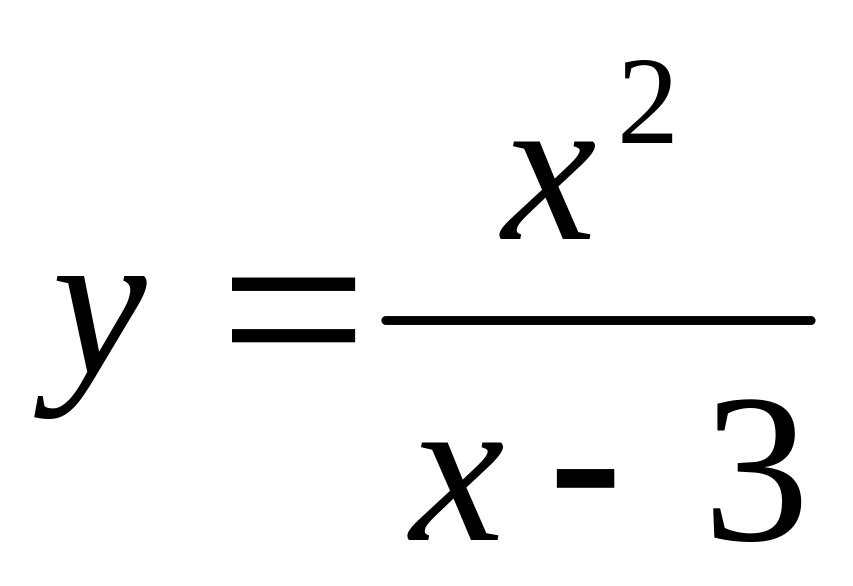 12)
12)
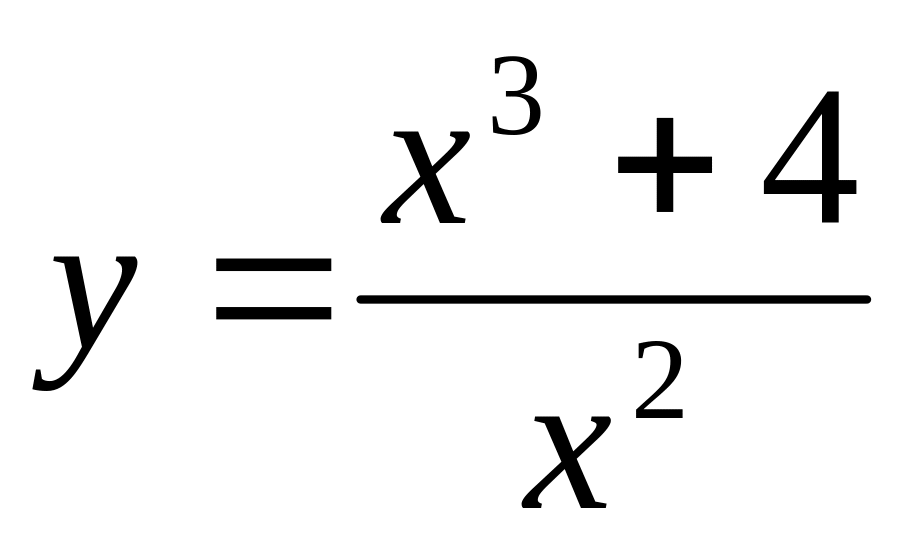
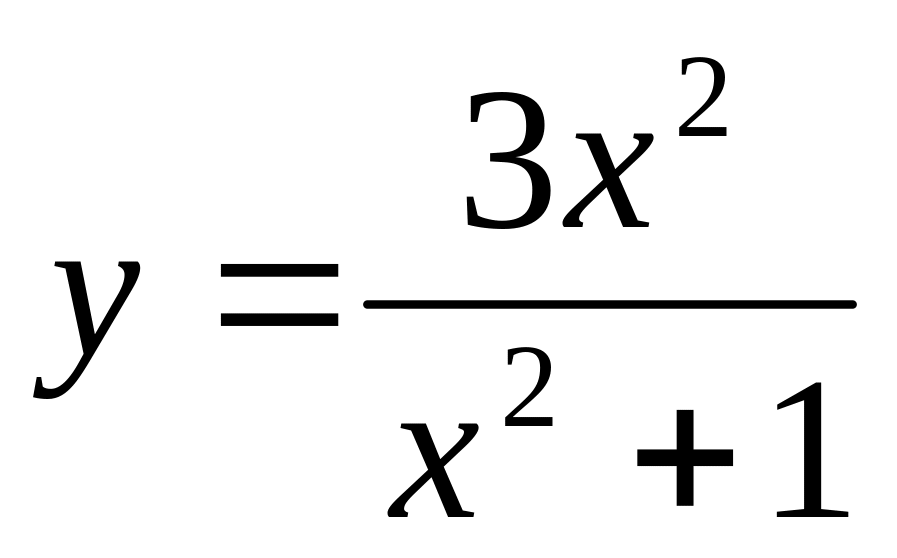 13)
13)
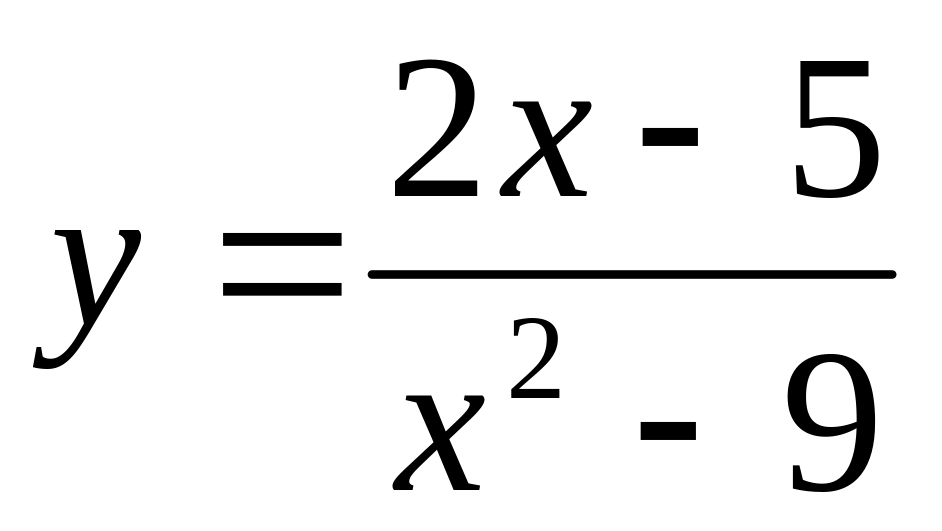
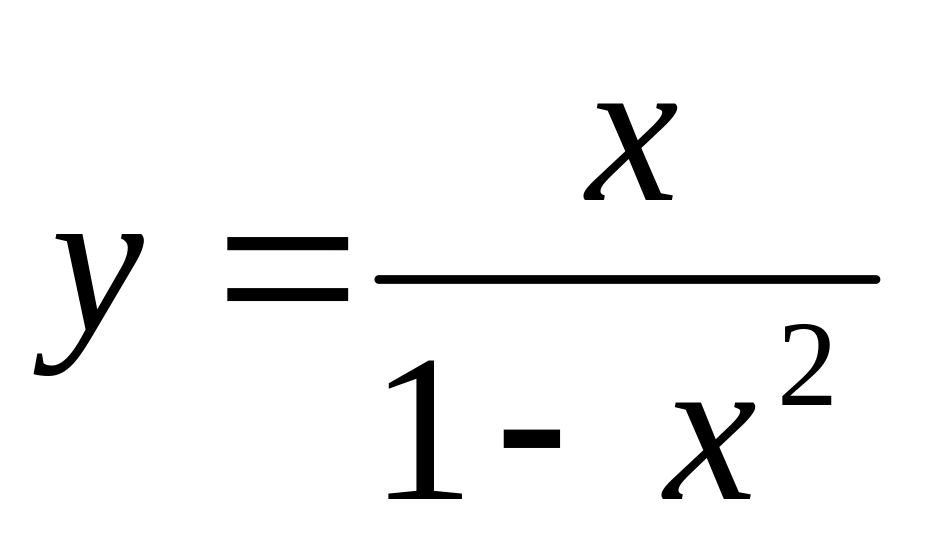 14)
14)
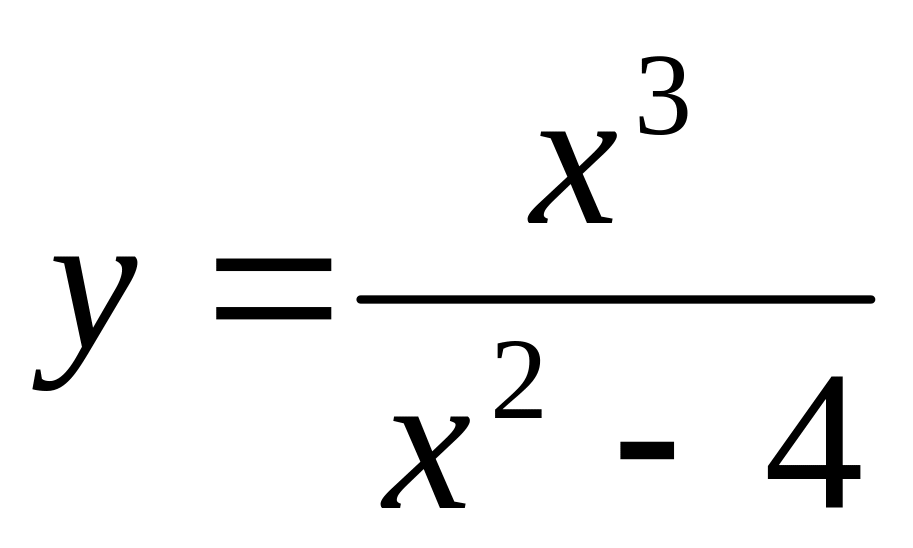
Контрольные вопросы:
Какая функция называется возрастающей? Убывающей?
Сформулируйте условия возрастания и убывания функции.
Что называется стационарной точкой? Критической точкой первого?
Сформулируйте первое достаточное условие существования экстремума.
Сформулируйте теорему Ферма.
Сформулируйте необходимое условие наличия точки перегиба
Алгоритм исследования и построения графика функции.
Практическая работа №6
« Неопределенный интгерал»
Цель работы: Сформировать навыки нахождения неопределенного интеграла методом непосредственного интегрирования, замены переменной, интегрирования по частям.
Теоретическая часть.
Пусть функция у=F(х) (1) имеет производную f(x), тогда ее дифференциал
dy=f(x)dx.
Функция (1) по отношению к ее дифференциалу называется первообразной.
Определение 1. Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:
F(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) = F2(x) + C.
Определение 2. Совокупность всех первообразных для функции f(x), определенных на некотором промежутке X, называется неопределенным интегралов от функции f(x) на этом промежутке и обозначается символом ∫f(x)dx.
![]() ,
,
где С – некоторая постоянная.
Определение 3. Геометрически неопределенный интеграл представляет собой семейство интегральных кривых, каждая из которых получается из любой другой кривой параллельным переносом вдоль оси Oy.
Свойства неопределенного интеграла
1)
(∫f(x)dx)′
=f(x). 4)
![]() .
.
2) d![]() . 5)
. 5)![]() .
.
3)
![]() .
.
Таблица некоторых интегралов
1)![]() ,
10)
,
10)
![]()
2)![]() ,
,
![]() 11)
11)
![]()
3)![]() 12)
12)
![]()
4)![]() 13)
13)
![]()
5)
![]() 14)
14)
![]()
6)![]() 15)
15)![]()
7)![]() 16)
16)![]()
8)![]() 17)
17)
![]()
9)![]() 18)
18)
![]()
Практическая часть
Непосредственное интегрирование
Этот метод в основном опираться на знания таблиц производных и первообразных.
Пример 1.
![]()
Решение. Применим правило интегрирования (4) и (5), а также табличные интегралы (1) и (2):
![]() .
.
Пример 2.
![]()
Решение. Применим табличный интерал (14), предворительно преобразав подинтегральное выражение.
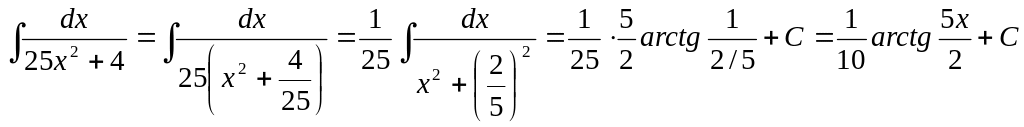 .
.
Замена переменной
Теорема:
Если требуется найти интеграл![]() ,
но сложно отыскать первообразную, то с
помощью замены x
= (t)
и dx
= (t)dt
получается:
,
но сложно отыскать первообразную, то с
помощью замены x
= (t)
и dx
= (t)dt
получается:
![]()
Пример 3.
![]() (3x-5)7dx
(3x-5)7dx
Решение. Положим, 3х-5=t, тогда 3dx=dt, dx=1/3dt. Следовательно,
(3x-5)7dx=
t7∙![]() dt=
dt=![]()
Пример 4.
![]()
Решение. sin5x dx= sin4x∙sin xdx= (1-cos2x)2∙sin xdx.
Положим, cos x=t, тогда -sin xdx=dt, или sin xdx= -dt. Следовательно,
sin5dx= - (1-t2)2dt= - (1-2t2+t4)dt= -t+2/3t3-1/5t5+C.
Пример 5. Найти неопределенный интеграл: .
Решение.
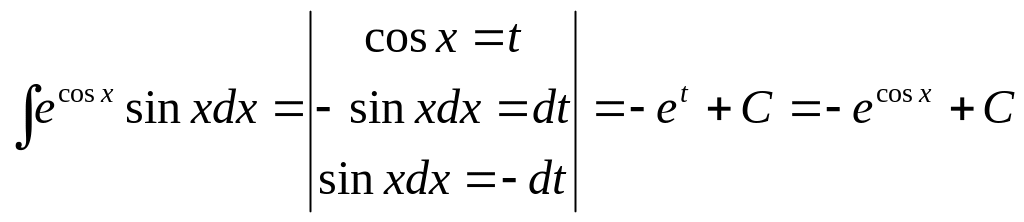 .
.
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv) = uv + vu
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав,
получаем:
![]() ,
,
![]()
или
![]() ;
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример
6.
![]() .
.
Решение.

![]()
Пример
7.![]() .
.
Решение.
![]()
![]() .
.
Как видно, нужно еще раз применить интегрирование по частям:
![]()
![]() .
.
![]()
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.
![]()
![]()
Таким образом, интеграл найден вообще без применения таблиц интегралов.
Практическая работа
Интегралы 1-3 найдите непосредственным интегрированием.
Интегралы 4-6 найдите подстановкой.
Интегралы 7-8 найдите интегрированием по частям.
В-1
|
Вариант 2 |
Вариант 3
|
Вариант 4 |
Вариант 5 |
Вариант 6
|
Вариант 7 |
Вариант 8 |
Вариант 9
|
Вариант 10 |
Вариант 11 |
Вариант 12
|
Вариант 13 |
Вариант 14 |
Контрольные вопросы:
Что называется первообразной функции?
Что называется неопределенным интегралом?
В чем заключается геометрический смысл неопределенного интеграла?
Свойства неопределенного интеграла.
В чем заключается смысл замены переменной в неопределенном интеграле?
В чем заключается смысл интегрирования по частям?
Практическая работа № 7
«Вычисление определенного интеграла».
Цель: сформировать навыки вычисления определенного интеграла.
Теоретическая часть
Пусть функция F(x) является первообразной для функции f(x) в некотором промежутке Х, а числа а и b принадлежат этому промежутку.
Определение.
Приращение
F(b)-F(a)
любой из первообразных функции F(x)+C
при изменении аргумента от х=а
до х=b
называется определенным интегралом
от а
до b
функции f(x)
и обозначается
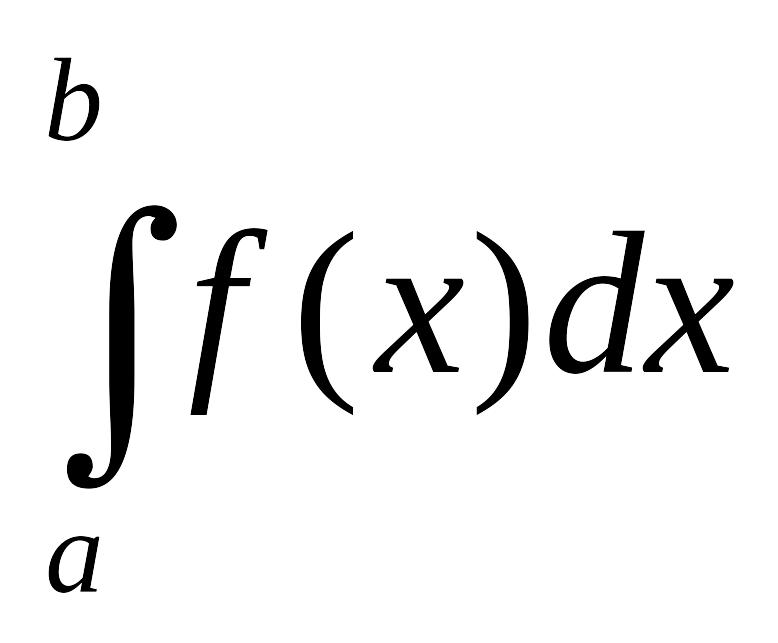 .
.
![]() – формула
Ньютона-Лейбница
– формула
Ньютона-Лейбница
Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов. Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов, которые были рассмотрены выше при нахождении неопределенных интегралов.
Точно так же применяются методы подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подынтегральную функцию, но и на пределы интегрирования. Заменяя переменную интегрирования, не забыть изменить соответственно пределы интегрирования.
Интегрирование по частям.
Если функции u = (x) и v = (x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:
![]()
Вывод этой формулы абсолютно аналогичен выводу формулы интегрирования по частям для неопределенного интеграла.
Основные свойства определенного интеграла
1)
![]()
2)![]()
3) Если
![]() то
то
![]()
4)
![]()
Практическая часть
Пример 1. Вычислить
определённый интеграл
![]()
Решение.
![]()
Пример 2.
![]()
Решение. Решим
методом подстановки. Пусть
![]() ,
тогда 2xdx=dt,
xdx=1/2dt.
Найдём новые пределы интегрирования,
подставляя в равенство
значения a=-1,
b=2.
,
тогда 2xdx=dt,
xdx=1/2dt.
Найдём новые пределы интегрирования,
подставляя в равенство
значения a=-1,
b=2.
![]() ,
,
![]() .
Следовательно,
.
Следовательно,
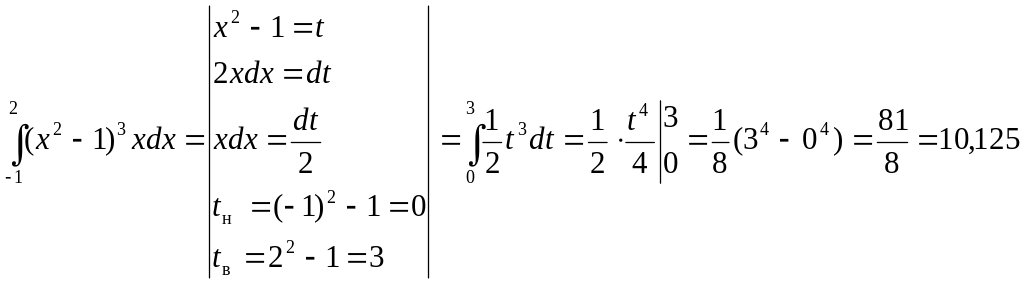
Пример 3.
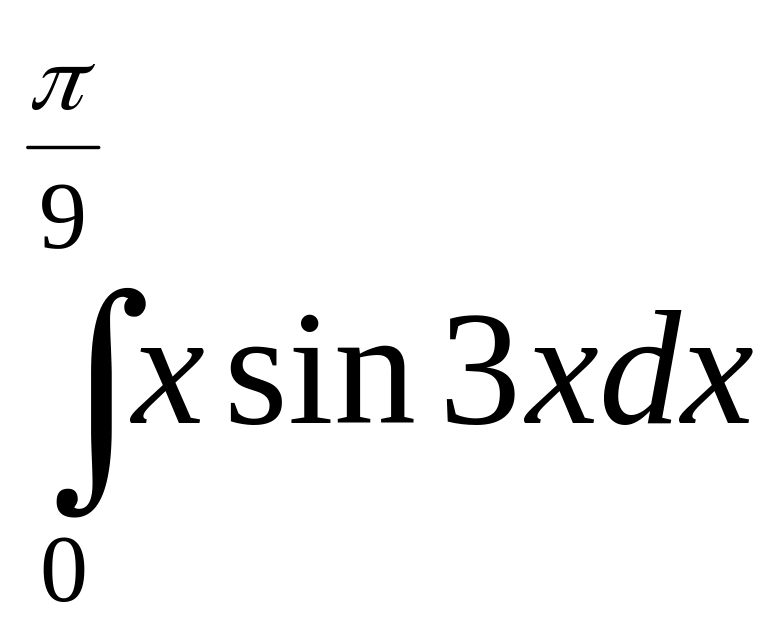
Решение. Интегрируем по частям.
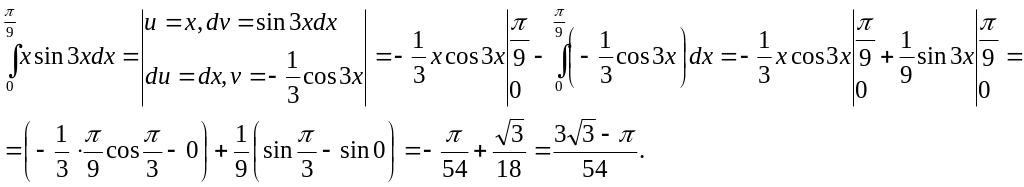
Практические задания
Вычислите интегралы:
1 вариант
1.
2.
3.
4.
5.
6.
|
2 вариант
1.
2.
3.
4.
5.
6.
|
3 вариант
1.
2.
3.
4.
5.
6.
|
4 вариант
1.
2.
3.
4.
5.
6.
|
5 вариант
1.
2.
3.
4.
5.
6.
|
6 вариант
1.
2.
3.
4.
5.
6.
|
7 вариант
1.
2.
3.
4.
5.
6.
|
8 вариант
1.
2.
3.
4.
5.
6.
|
9 вариант
1.
2.
3.
4.
5.
6.
|
10 вариант
1.
2.
3.
4.
5.
6.
|
11 вариант
1.
2.
3.
4.
5.
6.
|
12 вариант
1.
2.
3.
4.
5.
6.
|
Контрольные вопросы:
Что такое определенный интеграл?
Зависит ли значение определенного интеграла от выбора первообразной?
Чему равен определенный интеграл, если a=b?
Сформулируйте свойства определенного интеграла.
Практическая работа №8
«Приложение определенного интеграла»
Цель работы: Научится применять определенный интеграл для нахождения площади плоских фигур, объема тел вращения, пройденного телом пути, работу силы .
Теоретическая часть
Определенный интеграл широко применяется для нахождения различных физических и геометрических величин. Рассмотрим несколько задач.