
- •Дискретизация непрерывных сигналов
- •Комплект задач для самостоятельного решения по теме «Дискретизация непрерывных сигналов»
- •Задача №1.14
- •Задача №1.15
- •Задача №1.16
- •Комплект задач для самостоятельного решения по теме «Прямое z - преобразование»
- •Комплект задач для самостоятельного решения по теме «Обратное z - преобразование»
- •И мпульсная характеристика и системная
- •Комплект задач для самостоятельного решения по теме «и мпульсная характеристика и системная функция цифрового фильтра»
- •Комплексный коэффициент передачи,
- •Комплект задач для самостоятельного решения
- •Ачх и фчх цифрового фильтра»
- •Устойчивость цифровых фильтров
- •Системная функция цифрового фильтра описывается соотношением
- •Задача № 5.2
- •Комплект задач для самостоятельного решения по теме «Устойчивость цифровых фильтров»
- •1. Дискретизация непрерывных сигналов………………4
Дискретизация непрерывных сигналов
Спектр дискретной косинусоиды
На рисунке
1.1 представлена временная диаграмма
аналогового сигнала
![]() и вспомогательный сигнал u(t),
который представляет собой последовательность
прямоугольных импульсов с амплитудой
U и длительностью τ,
смещенных друг относительно друга на
интервал дискретизации TД.
и вспомогательный сигнал u(t),
который представляет собой последовательность
прямоугольных импульсов с амплитудой
U и длительностью τ,
смещенных друг относительно друга на
интервал дискретизации TД.

Рисунок 1.1 – Дискретизация аналоговой косинусоиды
Функция u(t) является периодической функцией времени, которую можно представить рядом Фурье
![]() ,
,
где
![]()
![]() .
.
Следовательно,
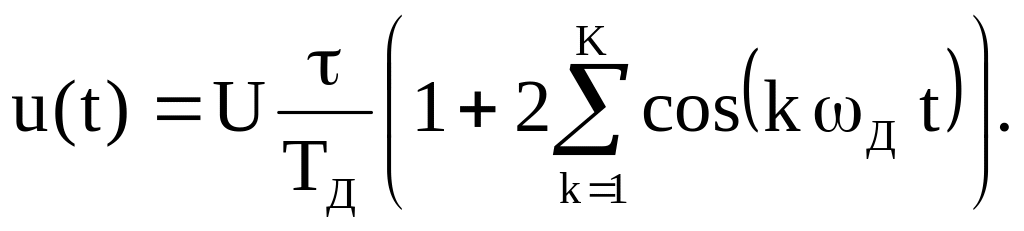
В последнем соотношении K – максимальный номер гармоники, при котором выполняется приведенное выше неравенство.
Дискретный сигнал определяется соотношением
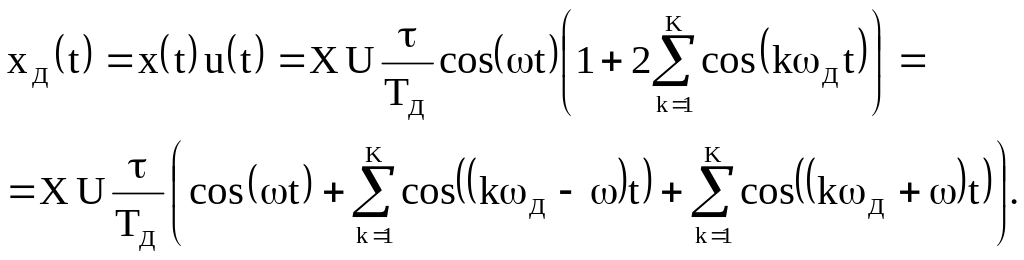
Из последнего соотношения видно, что
при дискретизации имеет место эффект
размножения спектра аналогового сигнала:
в спектре дискретной косинусоиды
содержатся составляющие с частотами![]() при k = 0, 1, 2, ...
Амплитуды этих составляющих одинаковы
и пропорциональны амплитуде X
аналоговой косинусоиды.
при k = 0, 1, 2, ...
Амплитуды этих составляющих одинаковы
и пропорциональны амплитуде X
аналоговой косинусоиды.
Задача №1.1
На входе дискретизатора действует аналоговый сигнал
![]() ,
где X=1, F=1
кГц.
,
где X=1, F=1
кГц.
Начертите с соблюдением масштаба амплитудный спектр сигнала до дискретизации (верхний график) и после дискретизации (нижний график), если частота дискретизации равна FД = 8 кГц. Спектр дискретного сигнала вычертить в интервале от 0 до 26 кГц, используя относительный масштаб по оси ординат.
Решение задачи №1.1
Составляющие спектра дискретного сигнала определим по формуле
![]() при k = 0, 1, 2, 3.
при k = 0, 1, 2, 3.
Получим частоты: 1, 7, 9, 15, 17, 23 и 25 кГц.

Рисунок 1.2 – Амплитудный спектр сигнала до и после дискретизации
Задача №1.2
На входе дискретизатора действует аналоговый сигнал
![]() ,
где X=1, f0=17
кГц.
,
где X=1, f0=17
кГц.
Начертите с соблюдением масштаба амплитудный спектр сигнала до дискретизации (верхний график) и после дискретизации (нижний график), если частота дискретизации равна FД = 8 кГц. Спектр дискретного сигнала вычертить в интервале от 0 до 26 кГц, используя относительный масштаб по оси ординат.
Решение задачи №1.2
Составляющие спектра дискретного сигнала определим по формуле
![]() при k = 0, 1, 2, 3, 4, 5.
при k = 0, 1, 2, 3, 4, 5.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
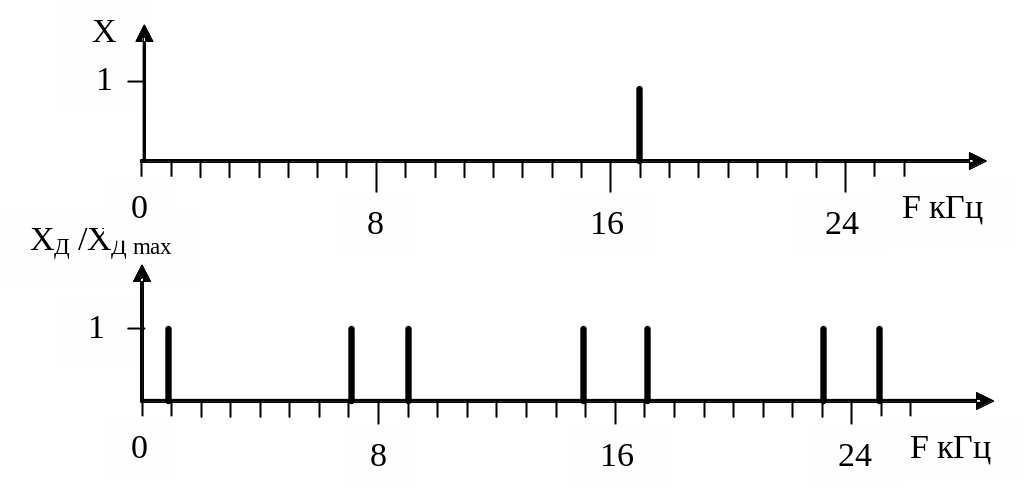
Рисунок 1.3 – Амплитудный спектр сигнала до и после дискретизации
На рисунке 1.4 приведены временные диаграммы сигналов на входе и выходе дискретизатора. Из него видно, что в периоде дискретного сигнала xД(t) содержится 17 периодов аналогового сигнала x(t), следовательно, при f0 = 17 кГц частота дискретного сигнала равна 1 кГц, т.е. частоте составляющей спектра дискретного сигнала, которая располагается в интервале частот от нуля до FД / 2 (в интервале Котельникова).
Сравните рисунок 1.4 с рисунком 1.1, из которого видно, что частота дискретного сигнала равна частоте аналогового сигнала, если частота аналогового сигнала находится в пределах интервала Котельникова.
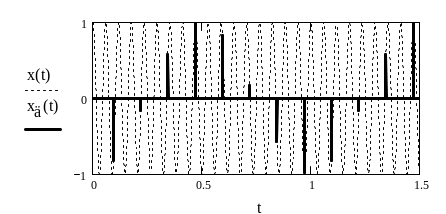
Рисунок 1.4 - Временные диаграммы сигналов на входе и
выходе дискретизатора
1.2. Дискретизация аналогового сигнала,
представляемого суммой гармоник
Пусть
![]()
где
![]()
Тогда
![]()
Вывод: спектр дискретного сигнала, полученного путем дискретизации аналогового сигнала в виде суммы гармонических составляющих, определяется путем суперпозиции спектров, соответствующих каждой гармонической составляющей исходного сигнала.
Задача №1.3
На входе дискретизатора действует аналоговый сигнал
![]() ,
,
где X1=1, F1=1 кГц , X2=0.5, F2=2 кГц.
Начертите с соблюдением масштаба амплитудный спектр сигнала до дискретизации (верхний график) и после дискретизации (нижний график), если частота дискретизации равна FД = 8 кГц. Спектр дискретного сигнала вычертить в интервале от 0 до 27 кГц, используя относительный масштаб по оси ординат.
Решение задачи №1.3
Составляющая спектра аналогового
сигнала с частотой F1
и амплитудой X1
порождает составляющие спектра
дискретного сигнала с частотами
![]() и равными амплитудами, пропорциональными
X1.
и равными амплитудами, пропорциональными
X1.
При k = 0, 1, 2, 3 получаем частоты: 1, 7, 9, 15, 17, 23, 25 кГц.
Составляющая спектра аналогового
сигнала с частотой F2
и амплитудой X2
порождает составляющие спектра
дискретного сигнала с частотами
![]() и равными амплитудами, пропорциональными
X1.
и равными амплитудами, пропорциональными
X1.
При k = 0, 1, 2, 3 получаем частоты:2, 6, 10, 14, 18, 22, 26 кГц.
Спектры аналогового и дискретного сигналов приведены на рисунке 1.5.
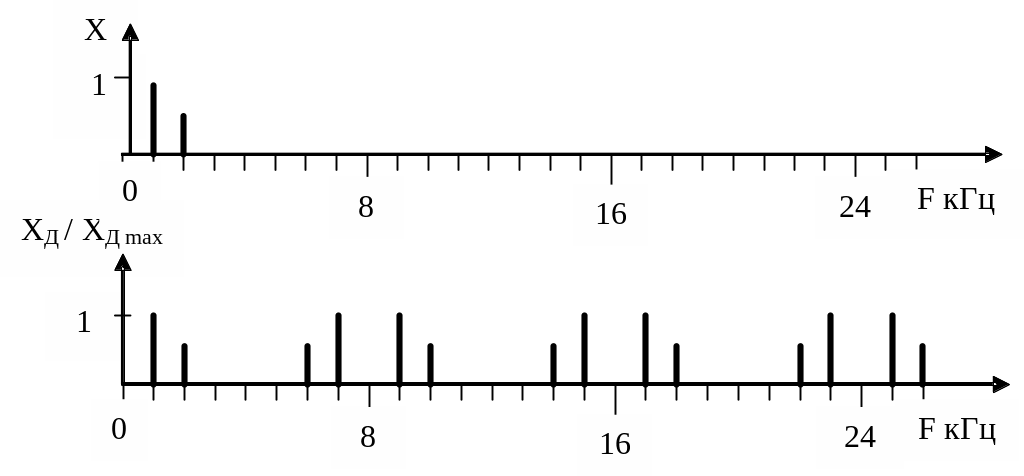
Рисунок 1.5 - Амплитудный спектр сигнала
до и после дискретизации
Задача №1.4
На входе дискретизатора действует аналоговый сигнал
![]() ,
,
где km=2, X0=1, X1= 0.5, X2 = 0.25, F0 =0, F1=0.5 кГц,
F2 =1 кГц, f0 =18 кГц.
Начертите с соблюдением масштаба амплитудный спектр сигнала до дискретизации (верхний график) и после дискретизации (нижний график), если частота дискретизации равна FД = 8 кГц. Спектр дискретного сигнала вычертить в пределах интервала частот от нуля до FД /2 (интервала Котельникова) в относительном масштабе по оси ординат.
Решение задачи №1.4
На рисунке 1.6 приведен амплитудный спектр исходного аналогового сигнала в соответствии с выражением для x(t).
При дискретизации в интервале Котельникова
появляются спектральные составляющие
за счет взаимодействия составляющих
спектра аналогового сигнала со второй
гармоникой частоты дискретизации:
![]()
![]()
![]() Амплитуды этих составляющих прямо
пропорциональны X0,
X1 и X2
соответственно.
Амплитуды этих составляющих прямо
пропорциональны X0,
X1 и X2
соответственно.
 Рисунок
1.6 – Амплитудный спектр сигнала
Рисунок
1.6 – Амплитудный спектр сигнала
до и после дискретизации
Задача №1.5
На входе дискретизатора действует аналоговый сигнал
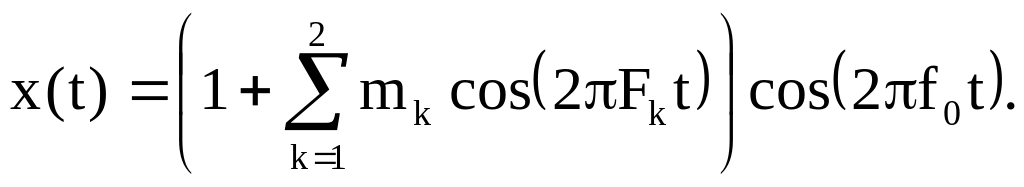
Начертите с соблюдением масштаба амплитудный спектр сигнала до дискретизации (верхний график) и после дискретизации (нижний график), если частота дискретизации равна FД = 8 МГц, m1 = 1, m2 =0.5, F 1 = 0.5 МГц,
F 2 = 1 МГц, f0 = 18 МГц. Спектр дискретного сигнала вычертить в пределах интервала Котельникова (от нуля до
FД / 2), используя относительный масштаб по оси ординат.
Решение задачи №1.5
Для определения спектра аналогового сигнала представим x(t) в виде суммы гармонических составляющих
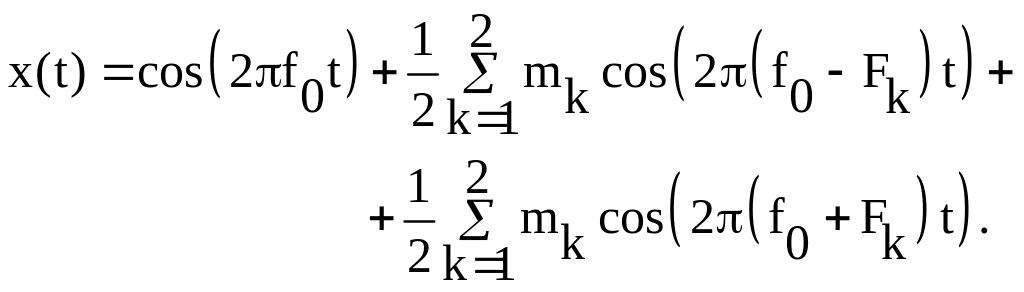
Из последнего соотношения видно, что в спектре аналогового сигнала содержатся составляющие с частотами
f0 = 18 МГц, f0-F1=17.5 МГц, f0-F2=17 МГц, f0+F1=18.5 МГц, f0+F2=19 МГц. Их амплитуды равны 1, 0.5, 0.25, 0.5, 0.25 соответственно. Амплитудный спектр этого сигнала приведен на рисунке 1.7.
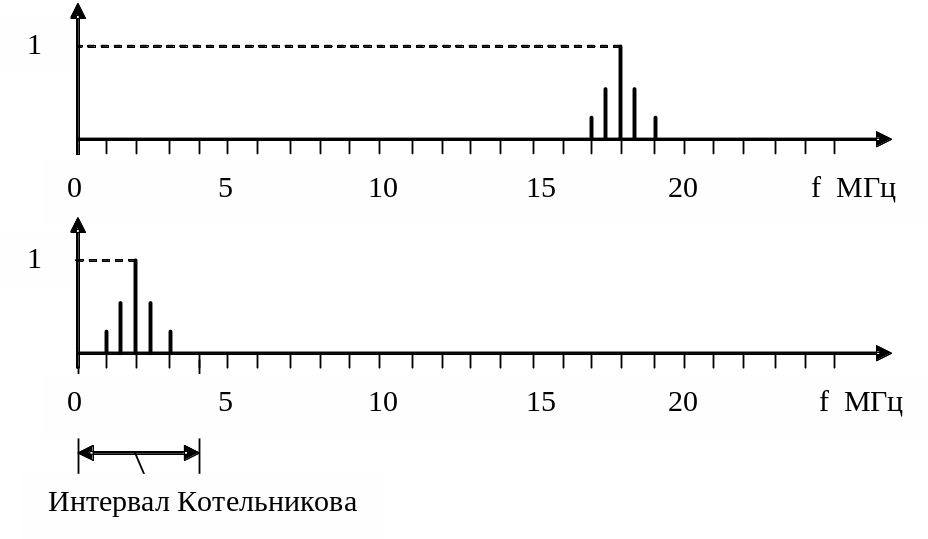 Рисунок 1.7 – Амплитудный спектр сигнала
Рисунок 1.7 – Амплитудный спектр сигнала
до и после дискретизации
В результате дискретизации в пределах интервала Котельникова появляются составляющие спектра на частотах:
![]()
![]()
![]()
![]()
![]()
1.3. Дискретизация апериодического аналогового
сигнала
Известно, что спектр
![]() апериодического
аналогового сигнала x(t)
определяется с использованием прямого
преобразования Фурье
апериодического
аналогового сигнала x(t)
определяется с использованием прямого
преобразования Фурье
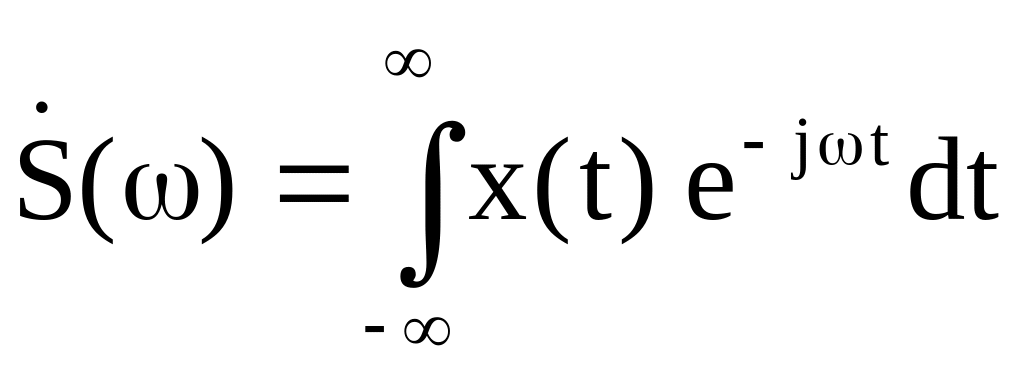 (1.1)
(1.1)
Для определения дискретного сигнала сначала преобразуем функцию u(t)

Воспользовавшись прямым преобразованием Фурье, найдем спектр дискретного сигнала
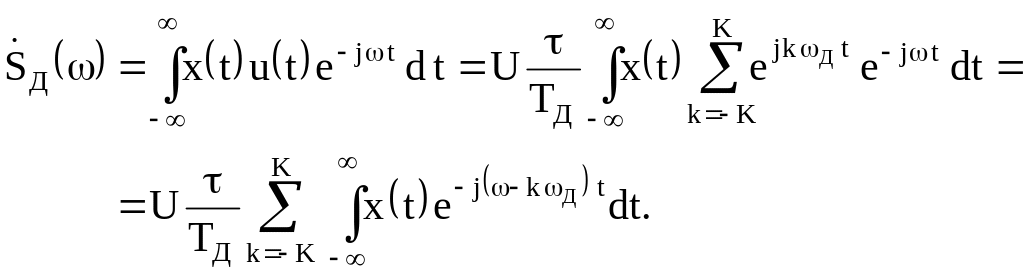
Сравнивая последнее соотношение с (1.1), выразим спектр дискретного сигнала через спектр аналогового сигнала
![]()
Таким образом, спектр дискретного
сигнала с точностью до постоянного
сомножителя Uτ/TД
равен сумме спектров аналогового
сигнала, сдвинутых на kωД.
На рисунке 1.8 показаны спектры
апериодического аналогового сигнала
до и после дискретизации как в области
положительных, так и в области отрицательных
частот. По оси абсцисс вместо круговой
частоты ω задаётся частота
![]()
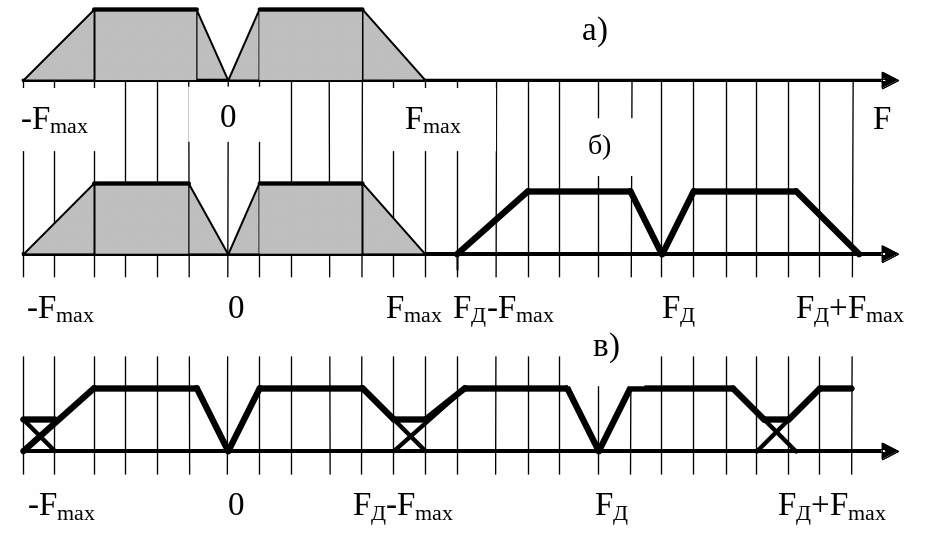 Рисунок
1.8 - Спектры апериодического аналогового
Рисунок
1.8 - Спектры апериодического аналогового
сигнала до дискретизации (а), после дискретизации при отсутствии (б) и при наличии (в) наложения спектров
Отличие спектров апериодического сигнала от линейчатых спектров периодического сигнала состоит в том, что спектральная плотность апериодического сигнала представляет собой непрерывную функцию частоты.
Как видно из рисунка 1.8 эффект наложения
спектров отсутствует, если
![]()
Из последнего неравенства следует известное условие выбора частоты дискретизации – теорема Котельникова
![]()
Задача №1.6
На рисунке 1.9 а показан спектр аналогового сигнала с минимальной частотой Fmin = 1 МГц, с максимальной частотой Fmax = 2 МГц. Частота дискретизации равна FД = 8 МГц. Начертите в относительном масштабе (по оси ординат) спектр дискретного сигнала в интервале частот от нуля до 27 МГц.
 Рисунок
1.9 - Спектральные диаграммы на входе и
выходе дискретизатора
Рисунок
1.9 - Спектральные диаграммы на входе и
выходе дискретизатора
Решение задачи №1.6
Минимальной частоте спектра аналогового
сигнала Fmin
в спектре дискретного сигнала
соответствуют частоты
![]() :
1, 7, 9, 15, 17, 23, 25 МГц при k =
0, 1, 2, 3.
:
1, 7, 9, 15, 17, 23, 25 МГц при k =
0, 1, 2, 3.
Максимальной частоте спектра аналогового
сигнала Fmax
в спектре дискретного сигнала соответствуют
частоты
![]() :
2, 6, 10, 14, 18, 22, 26 МГц при k =
0, 1, 2, 3.
:
2, 6, 10, 14, 18, 22, 26 МГц при k =
0, 1, 2, 3.
Форма сгустков спектра дискретного сигнала повторяет форму спектра аналогового сигнала с инверсией спектра или без нее.
Спектр сигнала на выходе дискретизатора приведен на рисунке 1.9 б.
