28. По семи территориям Уральского регионы за 1999 год получены следующие показатели (см. Табл.).
Район |
Расходы на покупку продовольственных товаров в общих расходах в %, Y |
Среднемесячная з/п одного работающего в тыс.рублей, X |
Удмуртская республика |
68,8 |
4,5 |
Свердловская область |
58,3 |
5,9 |
Башкортостан |
62,6 |
5,7 |
Челябинская область |
52,1 |
7,2 |
Пермская область |
54,5 |
6,2 |
Курганская область |
57,1 |
6,0 |
Оренбургская область |
51,0 |
7,8 |
Рассчитать параметры следующих функций:
а) линейной;
б) степенной
= a Xb
с) показательной = a bX.
Оценить качество этих регрессий.
29. [1, c.41] Пусть x
– нормально распределенная случайная
величина; μ – математическое ожидание
случайной величины x;
σ – стандартное отклонение;
– несмещенная оценка стандартного
отклонения; x1,…,
xn
– выборка объема n.
Показать, что величина
распределена по Стъюденту с (n
– 1) степенями свободы.
30. [1, c.43] Показать, что F-критерий, используемый для сравнения двух дисперсий, подчиняется распределению Фишера.
31. [1, c.46] По 10 наблюдениям
оценена зависимость между инфляцией и
безработицей в 1931–1940 гг. Получено:
i = 5.07 – 0.32u,
где i – инфляция,
u – безработица.
Оценена величина стандартной ошибки
Проверить
гипотезу H0: b
= 0 при α = 10%.
32. [1, c.54] Имеется выборка
из 60 наблюдений по индексу доходности.
При этом выборочное среднее
=
1,125 %, стандартное отклонение S
= 2,5 %. Каким будет 95 % доверительный
интервал?
33. Показать, что для регрессии с
одной переменной при нормальном
распределении остатков решение системы
,
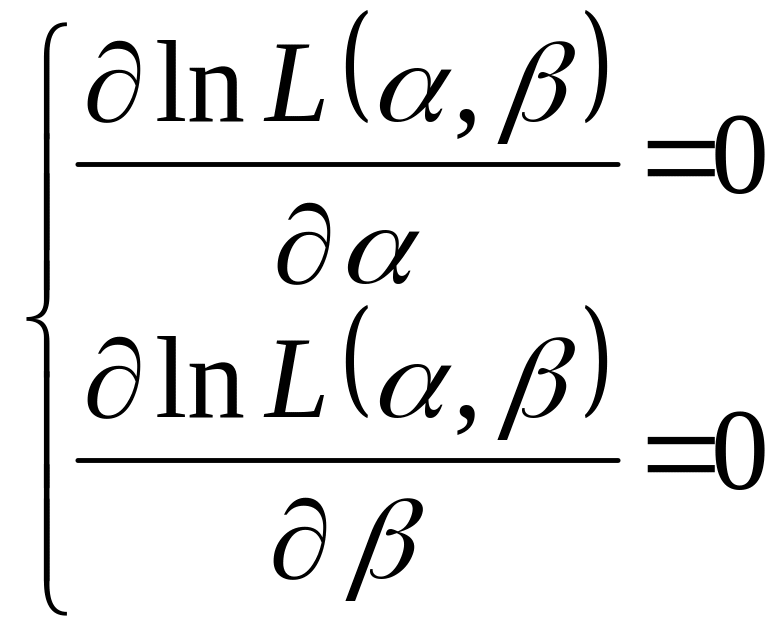где L(α,
β) – функция максимального
правдоподобия, сводится к системе (3.3)
(см. [1] с.30).
34. Найти собственные вектора,
собственные значения матрицы
.
Привести матрицу к диагональному виду:
.
35. «Большое домашнее задание» (БДЗ) - выполнение трех лабораторных работ по собственным исходным данным.
36. Реферат.
Задание для реферата.
Содержание реферата должно отражать следующие темы:
Метод наименьших квадратов (МНК):
а) трехшаговый МНК;
б) косвенный МНК;
в) обобщенный МНК.
Линейные регрессионные модели с гетероскедастичными и автокорреляционными остатками.
Регрессионные модели с переменной структурой (фиктивные переменные).
Каждый пункт из перечисленных выше не должен превышать объем 1 страницы и должен включать следующую информацию:
В чем смысл использования (для каждого вида МНК – отличие от обычного МНК).
Схема применения.
Пример.
Дополнительное задание для реферата:
Придумать 2-3 вопроса с выбором вариантов ответа (4-5 вариантов для каждого вопроса).
Придумать задачу (дать с решением).
В конце реферата дать список литературы с указанием ссылок по тексту реферата.