
Лекции по гетеропереходам / курс лекций физика и технология полупроводниковых наноструктур / 17_Кристаллическая структура
.pdf
Для поверхности кристалла, ориентированного в плоскости (100), элементарная ячейка поверхности:
1. |
Повернута на 450 (ориентирована вдоль направлений [0 |
|
1] и [011]) |
1 |
|||
2. |
Имеет постоянную решетки a / 2 |
||
Структура реконструированной поверхности обозначается числами m×n, указывающими, во сколько раз размер элементарной ячейки реконструированной поверхности больше нереконструированной ячейки в направлениях примитивных векторов поверхностной решетки (для (100) вдоль направлений [0 1 1] и [011]).
Например GaAs(100) 2x4 означает, что постоянная ячейки реконструированной поверхностной решетки больше в 2 раза вдоль [0 1 1] и в 4 раза вдоль [011].
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 17, стр. 11

[010]
[011]
[001]
[011]
a
a
2 a 

a
2
Структура поверхности (100) кристалла типа цинковой обманки.
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 17, стр. 12
Реконструкция поверхности может быть исследована с помощью дифракции быстрых электронов (ДБЭ), падающих под скользящими углами.
Условие дифракции электронов на кристаллической решетке в векторной записи:
k '= k +G
где k - волновой вектор падающего луча, kr' - волновой вектор рассеянного луча
Gr - произвольный вектор обратной решетки
(эквивалентно скалярной записи условия дифракции (закону Брэгга): 2dsin(Θ)=nλ)
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 17, стр. 13
Обратная решетка – воображаемая решетка, являющаяся образом (прямой) кристаллической решетки в обратном пространстве – построена из примитивных ячеек, примитивные вектора которых удовлетворяют условию:
arib j = 2πδij
где i, j = x,y,z,
δij =1 если i=j; 0 если i≠j
ai - примитивный вектор прямой решетки b j - примитивный вектор обратной решетки
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 17, стр. 14
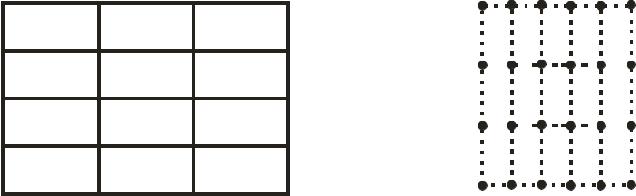
Кристаллическая решетка |
Обратная решетка |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aY |
bY=2π/aY |
|
|
aX |
bx=2π/aX |
Прямая и обратная двумерные прямоугольные решетки
Выполнение условия дифракции может быть проиллюстрировано геометрическим построением, известным как сфера Эвальда.
Сфера радиуса k=2π/λ. Вектор k совпадает с направлением падающего на кристалл луча и заканчивается на произвольном узле обратной решетки.
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 17, стр. 15

сфера Эвальда
Условие дифракции на кристалле, выполненное в построении Эвальда.
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 17, стр. 16

Падающий электронный луч испытывает дифракционное рассеяние на атомах кристаллической решетки. Вследствие малой глубины проникновения электронного пучка, вклад в дифракционную картину дают только приповерхностные атомы.
Длина волны де-Бройля для электрона связана с ускоряющим
напряжением V соотношением: |
|
|
||||
qV = |
h2 |
|
откуда получаем λ(nm) ≈ |
1,2 |
где V в вольтах |
|
2mλ2 |
V |
|||||
|
|
|
||||
При типичном |
для ДБЭ ускоряющем |
напряжении 10 кВ получаем |
||||
λ~1.2×10-2 нм, т.е. много меньше, чем типичные межатомные расстояния.
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 17, стр. 17

В геометрическом построении условия дифракции это означает, что сфера Эвальда имеет большой радиус по сравнению с периодом обратной решетки.
часть сферы Эвальда
В свою очередь это означает, что условие дифракции выполняется для нескольких близко расположенных узлов обратной решетки (нескольких направлений).
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 17, стр. 18
Возможность одновременного наблюдения нескольких дифракционных рефлексов позволяет судить о периоде решетки и ее изменении в направлении, перпендикулярном падающему лучу.
Реконструкция поверхности приводит к реконструкции и обратной решетки. Изменение периода поверхностной решетки в m раз эквивалентно изменению периода обратной решетки в 1/m раз.
При дифракции электронного луча это приводит к появлению в картине ДБЭ дополнительных (сверхструктурных) рефлексов, идущих в m и n раз чаще, чем рефлексы основной поверхностной ячейки.
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 17, стр. 19

картина дифракции на флуоресцентном экране
2x4
[001] |
|
[011] |
|
|||
|
|
|||||
|
|
|
||||
|
|
|
|
|
кристаллическая |
|
|
|
|
|
|
||
|
|
|
|
|
поверхность |
|
[011] |
||||||
|
||||||
падающий и зеркально-отраженный луч дифракционные лучи от основной решетки сверхструктурные дифракционные лучи
Возникновение картины дифракции быстрых электронов от реконструированной поверхности
А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 17, стр. 20
