Лекции по гетеропереходам / курс лекций физика и технология полупроводниковых наноструктур / 22_энергия локализации КТ

Энергия локализации носителей заряда в квантовой точке

Энергия локализации носителей заряда в квантовой точке, ∆, определяется положением уровней размерного квантования относительно краев зон материала матрицы.

Поскольку точное значение разрывов зоны проводимости и валентной зоны зачастую неизвестны, для приблизительных оценок полагают, что энергия локализации для электронов и дырок одинакова. Тогда:

где EE0-H0 энергия оптического перехода между основными состояниями электронов и дырок в КТ, которая может быть непосредственно измерена с помощью, например фотолюминесценции.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 22, стр. 1

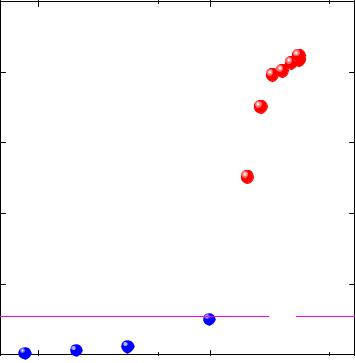
Энергия локализации уровня размерного квантования в КТ InAs в матрице

GaAs.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 22, стр. 2

Резкое возрастание энергии локализации носителей заряда (заглубление уровня размерного квантования) в островках InAs по сравнению с ожидаемым для случая двумерного распределения такого же количества InAs кажется парадоксальным, т.к. для дополнительного квантования в латеральном направлении можно ожидать уменьшения энергии локализации (выталкивания уровня).

Последнее справедливо, если сравниваются квантовая яма и квантовая точка одинаковой высоты. Однако в реальном случае имеет место перераспределение очень узкой ямы (толщиной около 0.6 нм) в более протяженные в вертикальном направлении пирамиды (~ 5нм), что и приводит к понижению энергии квантования.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 22, стр. 3

Достаточно большая энергия локализации существенна для того, чтобы концентрация носителей заряда, находящихся в матрице, была мала по сравнению с концентрацией носителей непосредственно в самой активной области. Это особенно важно для КТ, поскольку полное количество носителей заряда, которое может находиться на состояниях КТ, ограничено поверхностной плотностью точек.

Nmatrix << nQD

Концентрация носителей в матрице задается объемной плотностью

мкм) и положением квази-уровня Ферми F

∞

Nmatrix = ∫ρ(E)Wf (F, E)dE

EC

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 22, стр. 4

функция Ферми, которая для невырожденного полупроводника может быть аппроксимирована экспоненциальной зависимостью;

EC – край зоны проводимости матрицы

EC = ∆ если энергия отсчитывается от уровня КТ

F отсчитывается от уровня КТ (=0 при выполнении условия инверсии заселенности КТ)

Тогда

Безразмерный интеграл в правой части сходится и приближенно равен 0.9)

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 22, стр. 5

При достижении условия прозрачности для КТ квази-уровень Ферми проходит через уровень КТ. Тогда F=0

Отсюда условие для энергии локализации уровня КТ записывается в виде:

∆ > kBT ln Nneff W

QD

Учитывая типичные значения для эффективной плотности состояний матрицы (~1018 см-3), ширины слоя матрицы (0.2 мкм) и плотности массива квантовых точек (~5×1010 см-2) получаем, что энергия локализации должна составлять не менее 150-200 мэВ.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 22, стр. 7

Для достижения порога лазерной генерации требуется более высокая концентрация носителей в КТ, что эквивалентно более высокому значению энергии Ферми.

Взаимосвязь между энергией Ферми, F, вероятностью заполнения состояний КТ, f0, концентрацией носителей заряда в КТ, NQD, и усилением G, записывается следующим образом:

(поскольку мы полагаем, что все КТ массива характеризуются одинаковым уровнем энергии, который мы выбрали за ноль).

NQD = ∫ρQD (E) f (E, F)dE = 2 f0nQD

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 22, стр. 9

Концентрация носителей заряда в массива КТ равна произведению удвоенной поверхностной плотности массива, умноженной на вероятность заполнения.

G = Gsat (2 f0 −1)

Пороговая вероятность заполнения состояний КТ, fth, и пороговая концентрация носителей в массиве КТ, Nth, достаточные для преодоления полных оптических потерь, α, определяется как:

половина состояний КТ, а при максимальных потерях, которые могут быть преодолены (Gsat) заполнены все состояния КТ.

А.Е.Жуков, Физика и технология полупроводниковых наноструктур, гл. 22, стр. 10