§. Основные свойства несобственного интеграла.

А. Множество функций, интегрируемых на промежутке в несобственном смысле, образуют линейное пространство со стандартно введенными операциями сложения функций и умножения функции на число, а несобственный интеграл по этому промежутку является линейным функционалом на указанном линейном пространстве. Это значит, что

1). 

2). , где значок означает если интегралы стоящие в правой части существуют (сходятся) и конечны, то интеграл стоящий в левой части существует, конечен и равен указанной в левой части линейной комбинации.

Б. Монотонность. Несобственный интеграл есть монотонный функционал на ;

Т. Несобственный интеграл от неотрицательной функции неотрицателен, т.е.

.

  

. ▲

Отсюда следует собственно монотонность несобственного интеграла

.

В. Интегрируемость по подпромежутку. .

Г. Аддитивность. .

Д. Формула Ньютона–Лейбница. Рассмотрим функцию . Тогда

1) F – непрерывна на . 2) F – дифференцируема п. в. на .

3) , исключая не более чем счетное множество точек.

Тогда для несобственного интеграла справедлива формула, аналогичная формуле Ньютона–Лейбница для определенного интеграла .

Е. Формула интегрирования по частям. Пусть дифференцируемы на , причем, хотя бы одна из них непрерывно дифференцируема, то: .

Ж. Замена переменной в несобственном интеграле. Если функция непрерывно дифференцируема и строго монотонна, то

.

З. Необходимое, но недостаточное условие сходимости несобственного интеграла.

Для сходимости интеграла необходимо, чтобы интегралы по всем конечным подпромежуткам промежутка интегрирования существовали и были конечны. Однако выполнение такого условия недостаточно для сходимости интеграла. Если ввести в рассмотрение функцию , то сходимость интеграла означает .

Пример. существует для любого конечного промежутка , но =

= = = . Однако последний предел не существует и, следовательно, .

И. Несобственно интегрируемая функция должна быть непрерывна п. в. на .

Если , то она непрерывна на почти всюду.

К. Если п.в. на и существует, то он равен нулю.

§. Критерий Коши сходимости несобственного интеграла.

Рассмотрим несобственный интеграл с одной особой точкой ω на конце промежутка интегрирования. Интеграл сходится, тогда и только тогда, когда

.

 Это, собственно говоря, критерий Коши для того, чтобы существовал предел . ▲

§. Абсолютная сходимость.

Def: Несобственный интеграл называется сходящимся абсолютно, если сходится интеграл от модуля подынтегральной функции .

Т⁰. Абсолютно сходящийся интеграл сходится.

 Пусть интеграл сходится  (по критерию Коши)

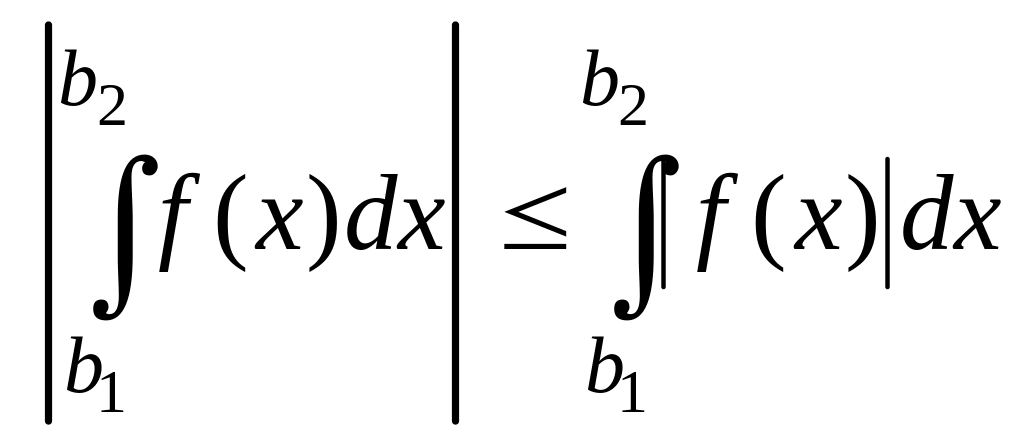, но и,

следовательно, . ▲

Т⁰. Для интегралов от неотрицательных функций сходимость эквивалентна ограниченности в совокупности интегралов по всем замкнутым промежуткам и, при этом, если

 .

 Пусть  . Кроме того, функция не убывает

. Поэтому . ▲

Т⁰. Замена переменной со строго монотонной функцией. Если строго монотонная функция, то замена сохраняет абсолютную сходимость интеграла.

. Если функция не убывающая, то и, следовательно,

.

Крайние члены этой цепочки одновременно сходятся или расходятся. ▲

Замечание: Интегрирование по частям в общем случае не сохраняет абсолютную сходимость.

Пример: Рассмотрим . При этом, интеграл справа сходится абсолютно, а интеграл слева не сходится абсолютно. Мы это установим несколько позже.