Раздел 2. Применение определенного интеграла в геометрических и физических задачах.

Замечание: В полной мере теория приложений может быть разработана с применением кратных, криволинейных и поверхностных интегралов. Поэтому в излагаемом разделе нецелесообразно превышать некоторый уровень математической строгости. Навыки работы в этом направлении – вот что будет для нас главным в этом разделе.

§. Вычисление площадей плоских фигур.

П

лощадь криволинейной фигуры может быть найдена из уже известного геометрического смысла определенного интеграла. .

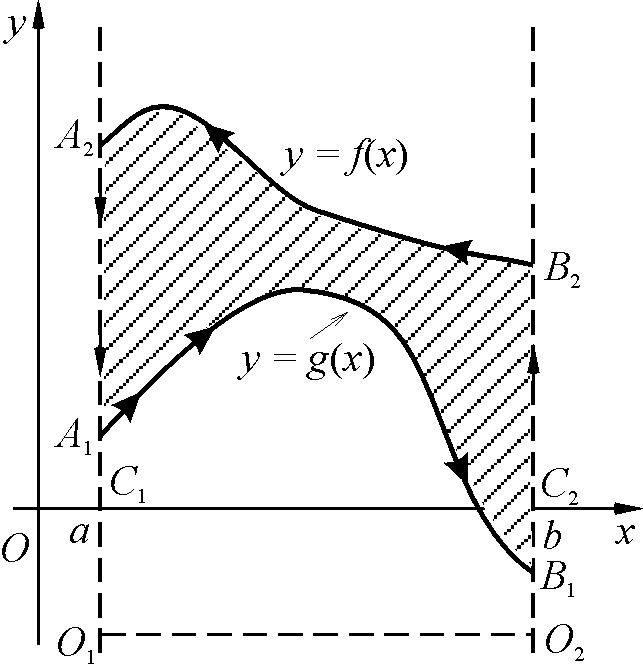
Для дальнейших приложений это будет удобно записать в виде криволинейного интеграла.

(Все связанное с криволинейным интегралом, пока следует рассматривать только как удобную форму записи).

=

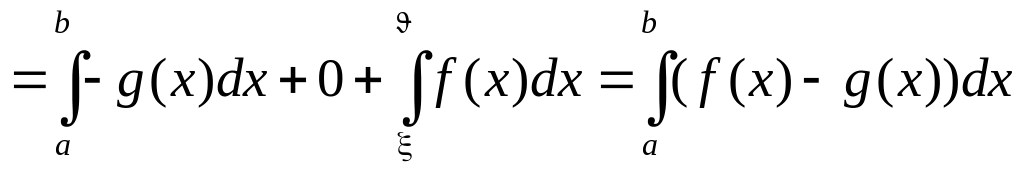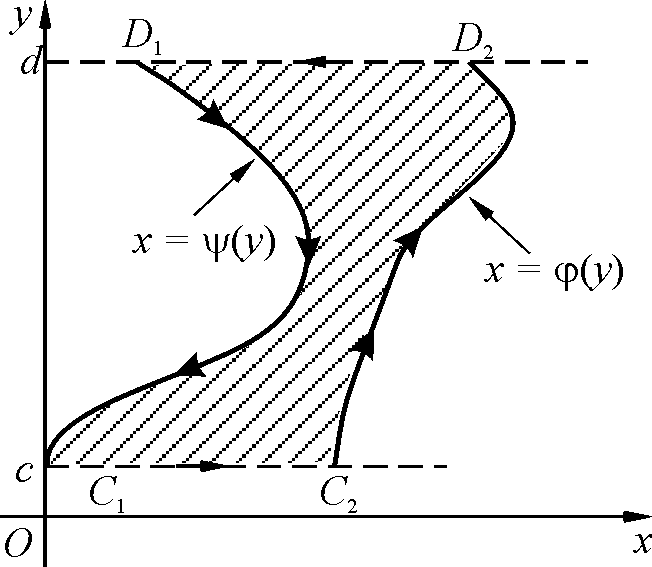
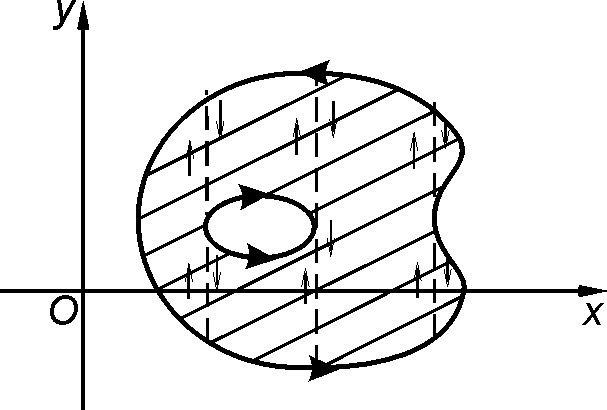
. Для областей с конфигурацией как на втором рисунке более удобной является формула . При обходе областей сложной конфигурации можно разбивать ее на более простые области (пример указан на третьем рисунке) и для вычисления площадей плоских фигур пользоваться либо формулой , либо формулой , либо комбинированной формулой .

Если функция, определяющая границу области, задана параметрически , то последняя формула принимает вид .

Формула для нахождения площади фигуры, граница которой задана в полярных координатах , имеет вид и получена суммированием площадей элементарных криволинейных треугольников (рис. б, см. следующий параграф) .

§. Вычисление длин дуг плоских кривых.

Формула для нахождения длина дуги кривой получается суммированием длин элементарных дуг. Длина элементарной дуги в декартовых координатах может быть найдена по формуле П

ифагора (рис. а) .

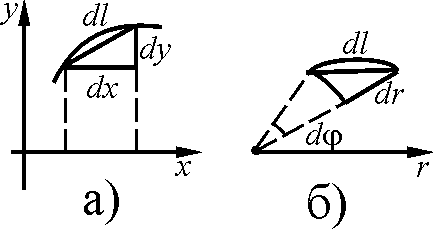
*. Если кривая задана явно , то 

*. Если же кривая задана явно , то 

*. Для кривой, заданной параметрически, , получим .

*. В полярной системе координат (рис. б) . В различных частных случаях

.

И, наконец, формула для нахождения длины дуги кривой, записанная через криволинейный интеграл . Эта формула, с учетом способа задания кривой, может быть переписана с помощью интеграла Римана, например .

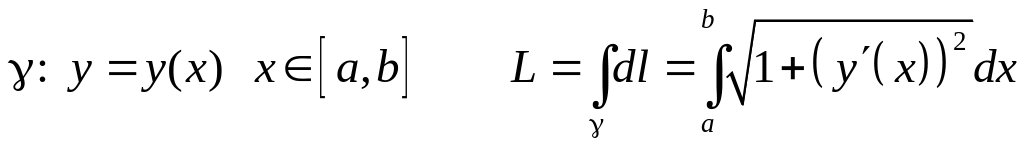Пример: Найти площадь и длину дуги эллипса с полуосями а и b.

Зададим эллипс параметрическим уравнением . Тогда

1). .

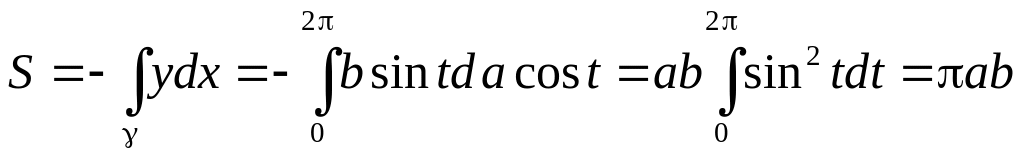2). =

= = … … . Получившийся интеграл – эллиптический интеграл и не выражается через элементарные функции. Его значение может быть найдено численными методами, например, методом прямоугольников, трапеций или Симпсона (они будут рассмотрены позже). Также его значение может быть найдено в справочниках по специальным функциям (например, М. Абрамовиц, И. Стиган).

§. Криволинейные интегралы I-го рода.

Для кривой определим .

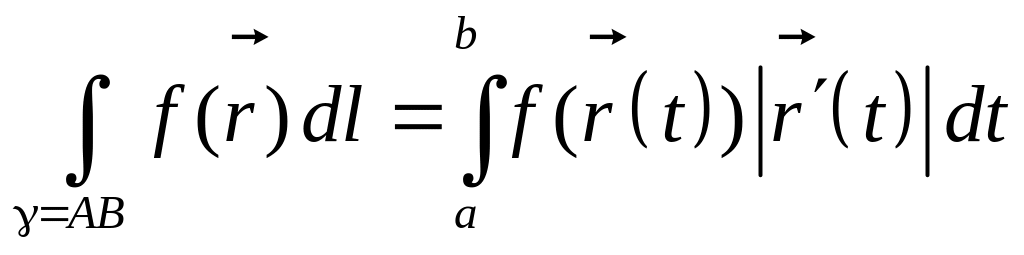Так определенный интеграл называется криволинейным интегралом первого рода.

Физический смысл криволинейного интеграла первого рода – если функция определяет линейную плотность масс на кривой, то определяет массу кривой.

Свойства криволинейного интеграла:

1. Определение интеграла корректно, т. е. не зависит от способа параметризации;

2. Интеграл не зависит от ориентации, т.е. при изменении направления обхода дуги интеграл не изменяется;

3. Интеграл линеен, т.е. интеграл от линейной комбинации функций равен линейной комбинации интегралов от этих функций.;

4. Интеграл есть аддитивная функция дуги кривой, т.е. интеграл по всей дуге равен сумме интегралов по ее отдельным частям;

5. Интеграл от единицы численно равен длине кривой;

6. Интеграл монотонен, т. е. интеграл от неотрицательной функции неотрицателен.

§. Вычисление площадей поверхностей вращения.