
125 Кібербезпека / Магістр (вступні питання)
.pdf
На наступному кроці до кожного неголовного рядка (в даному випадку це будуть рядки під номером один, два та три) матриці додамо головний рядок (третій рядок) помножений на відповідний для нього множник  . Даний процес описується формулою (4). В результаті отримаємо матрицю наступного виду:
. Даний процес описується формулою (4). В результаті отримаємо матрицю наступного виду:
Далі, викреслюючи четверту колонку і третій (головний) рядок, отримаємо матрицю  , яка складається з меншого на одиницю числа рядків і колонок:
, яка складається з меншого на одиницю числа рядків і колонок:
Після цього переходимо до етапу номер два, і над отриманою матрицею  повторюємо тіж операції, а саме:
повторюємо тіж операції, а саме:
1.Вибираємо головний елемент:  .
.
2.Для першого і другого рядка матриці обчислюємо множники  :
:
3.До кожного неголовного рядка (в даному випадку це будуть рядки під номером один та два) матриці  додамо головний рядок (третій рядок) помножений на відповідний для нього множник
додамо головний рядок (третій рядок) помножений на відповідний для нього множник  . Результатом виконання даного кроку буде матриця виду:
. Результатом виконання даного кроку буде матриця виду:
4.Далі, викреслюючи третій стовпець і третій (головний) рядок, отримаємо матрицю  , після чого, переходимо до третього етапу:
, після чого, переходимо до третього етапу:
Етап номер три:
1.Вибираємо головний елемент:  .
.
2.Для другого рядка матриці обчислюємо множник 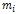 :
:
3.До кожного неголовного рядка (в даному випадку це буде рядок під номером два) матриці  додамо головний рядок (перший рядок) помножений на відповідний для нього множник
додамо головний рядок (перший рядок) помножений на відповідний для нього множник  . Результатом виконання даного кроку буде матриця виду:
. Результатом виконання даного кроку буде матриця виду:
4.Далі, викреслюючи другий стовпець і перший (головний) рядок, отримаємо матрицю  , яка складається з одного рядка і двох колонок:
, яка складається з одного рядка і двох колонок:
На цьому процедуру приведення матриці до трикутного вигляду можна вважати завершеною. Переходимо до визначення невідомих  . Для цього, як уже зазначалося вище, об'єднуємо в систему, починаючи з останнього, який входить в матрицю
. Для цього, як уже зазначалося вище, об'єднуємо в систему, починаючи з останнього, який входить в матрицю  , всі головні рядки. В результаті отримуємо систему з допомогою якої, легко знаходимо невідомі:
, всі головні рядки. В результаті отримуємо систему з допомогою якої, легко знаходимо невідомі:

Зауваження: для отримання системи трикутної форми, за бажанням можна зробити відповідну перестановку рядків та колонок. Крім того відмітимо, що при перестановці стовпців змінюється порядок невідомих, тому в цьому випадку треба запам'ятати новий їх порядок. Для цього, як правило, формується масив з елементами, відповідними порядку невідомих. Спочатку там повинен бути забезпечений порядок невідомих, наприклад, як у нашому випадку від 1 до 4. Після цього, у міру перестановки стовпців, відповідні елементи даного масиву теж треба поміняти місцями.
105. Інтерполяція і наближення функцій
Так, якщо в результаті інженерного або наукового експерименту отримана
система точок:  , то дуже часто виникає задача пошуку аналітичної залежності, яка б зв‗язувала експериментальні дані у вигляді
, то дуже часто виникає задача пошуку аналітичної залежності, яка б зв‗язувала експериментальні дані у вигляді
аналітичної функції |
. Для розв‘язування цієї задачі за допомогою чисельних |
|||||
методів на ЕОМ використовуються два підходи: |
|
|
|
|||
1. Інтерполяція – підхід, |
за |
допомогою |
якого |
отримують |
аналітичні |
|
залежності табличних функцій за умови, що аналітична функція |
повинна |
|||||
проходити через всі задані експериментальні точки. |
|
|
||||
2. Апроксимація – підхід, |
за |
допомогою |
якого |
знаходиться |
аналітична |
|
функція  , що ―найкращим чином‖ наближається до заданої табличної функції. Звичайно ―найкращим чином‖ – це критерій, в якості якого використовується критерій середньо квадратичного відхилення (СКВ), заснований
, що ―найкращим чином‖ наближається до заданої табличної функції. Звичайно ―найкращим чином‖ – це критерій, в якості якого використовується критерій середньо квадратичного відхилення (СКВ), заснований
на тому, що сума квадратів відхилень аналітичної функції |
від |
експериментальної  (при і=0, 1, …, k) повинна бути мінімальною:
(при і=0, 1, …, k) повинна бути мінімальною:
На |
рисунку |
5.1 |
представлена класифікація |
відомих |
методів |
|||
наближення табличних |
|
функцій, |
призначених для |
пошуку аналітичної |
||||
залежності |
, |
|
яка |
б |
зв‗язувала |
експериментальні |
||
дані  , отримані в результаті інженерного або наукового експерименту.
, отримані в результаті інженерного або наукового експерименту.

Рисунок 5.1 – Класифікація чисельних методів наближення табличних функцій
5.2 Математична постановка задачі інтерполювання
В економіці і техніці постійно приходиться зіштовхуватися з необхідністю
обчислення значень функції  в точках
в точках  , відмінних від значень аргументу, фіксованих в таблиці експериментальних досліджень. Крім того, в
, відмінних від значень аргументу, фіксованих в таблиці експериментальних досліджень. Крім того, в
деяких випадках, незважаючи на те, що аналітичний вираз функції  відомий, він є занадто складним і незручним для подальших математичних
відомий, він є занадто складним і незручним для подальших математичних
перетворень. Подібні задачі формалізуються як задачі інтерполювання. |
||||||
Нехай |
на |
відрізку |
|
функція |
задана |
системою |
точок |
|
, |
де |
значення |
називаються вузлами |
|
інтерполяції. Необхідно знайти аналітичну залежність |
, співпадаючої у вузлах |
|||||
інтерполяції |
зі |
значеннями |
заданої |
функції, |
||
тобто |
|
|
|
|
Процес |
обчислення |
значень |
функції |
в точках |
, |
відмінних |
від вузлів |
інтерполяції, |
називають інтерполюванням функції |
(рисунок 5.1). |
|
|
|||
Якщо аргумент знаходиться за межами відрізка інтерполювання |
, то |
|||||
задача |
визначення |
значення |
функції |
в |
точці |
|
називається екстраполюванням. |
|
|
|
|
|
|
Слідує відмітити, що задача інтерполювання стає однозначною, якщо в якості
функції |
вибрати |
багаточлен |
степені |
не |
вище |
n, |
такий, |
|||
що |
|
|
. Багаточлен |
|
, що задовольняє цим умовам, |
|||||
називають інтерполяційним |
багаточленом, |
а |
відповідні |
формули |
– |
|||||
інтерполяційними формулами. |
|
|
|
|
|
|
|
|
||
Рисунок 5.2 – Геометрична інтерпретація інтерполяції табличної функції
У випадку, коли  береться з класу степеневих функцій, інтерполяція називається параболічною. Цей спосіб наближення ґрунтується на тому, що на
береться з класу степеневих функцій, інтерполяція називається параболічною. Цей спосіб наближення ґрунтується на тому, що на
невеликих відрізках експериментальна функція  може бути достатньо добре апроксимована параболою певного порядку. Якщо в якості інтерполяційної функції використовувати багаточлен виду:
може бути достатньо добре апроксимована параболою певного порядку. Якщо в якості інтерполяційної функції використовувати багаточлен виду:
(5.1)
то така інтерполяція називається степеневою

Інколи доцільно використати інші види інтерполяції. Якщо функція, що
досліджується,  – періодична, то в якості інтерполяційної функції
– періодична, то в якості інтерполяційної функції 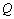 (
(  ) вибирають тригонометричну, наприклад, виду:
) вибирають тригонометричну, наприклад, виду:
(5.2)
і така інтерполяція називається тригонометричною. В деяких в якості інтерполяційної функції  (
(  ) вибирають раціональні функції.
) вибирають раціональні функції.
При інтерполюванні виникає ряд задач:
1. вибір найбільш зручного способу побудови інтерполяційної функції для кожного конкретного випадку;
2. оцінка |
похибки |
при заміні |
|
інтерполяційною |
функцією |
на |
відрізку |
, оскільки |
функції |
та |
співпадають |
тільки у |
вузлах |
інтерполяції 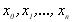 ; 3. оптимальний вибір вузлів інтерполяції для отримання мінімальної похибки.
; 3. оптимальний вибір вузлів інтерполяції для отримання мінімальної похибки.
Для задачі інтерполювання важливим є визначення того, як повинна вести себе інтерполяційна функція між заданими точками, так як ці точки можуть бути інтерпольовані множиною різноманітних функцій, і необхідно мати певний критерій вибору. Звичайно критерій формується в термінах гладкості та простоти. Більшість інтерполяційних функції генеруються лінійними комбінаціями
найпростіших функцій. Лінійні комбінації одночленів  формують степеневі
формують степеневі
поліноми, |
лінійні |
комбінації |
тригонометричних |
функцій |
||
формують тригонометричні поліноми, |
використовуються |
також лінійні |
||||
комбінації |
експонент |
. Найбільш |
важливим класом |
інтерполяційних |
||
функцій є множина алгебраїчних поліномів. Поліноми мають переваги з точки зору алгоритмізації, тому що їх значення легко обчисляти, додавати, перемножувати, інтегрувати чи диференціювати. Важливою властивістю
поліномів є |
те |
що якщо с – |
константа, |
а p(x)- поліном, |
то поліномами будуть |
і p(cx) і p(x+c) |
|
|
|
|
|
Клас |
інтерполяційних |
функції |
обирають, використовуючи теорему |
||
Вейерштраса: |
|
|
|
|
|
Якщо f(х) – |
неперервна |
на кінцевому інтервалі |
функція, то для |
||
любого  існують поліном pn(x) ступеня n такий, що
існують поліном pn(x) ступеня n такий, що  .
.
5.2.1 Інтерполяційний багаточлен Лагранжа
Найбільш загальною формулою параболічного інтерполювання є інтерполяційна формула Лагранжа. Задача параболічного інтерполювання в
цьому випадку |
формулюється |
наступним чином: на |
відрізку |
у |
вузлах |
|
інтерполяції |
задається функція |
своїми |
значеннями |
|
||
|
|
, |
|
|
|
|
необхідно |
побудувати |
багаточлен |
так, |
щоб |
у |
вузлах |
інтерполяції |
його значення співпадали зі значеннями заданої функції, |
|||||
тобто |
…, |
Слід відзначити, що в такій постановці |
||||
задачі вузли інтерполяції |
можуть бути довільно розташовані один від |
|||||
одного на відрізку  , іншими словами, вузли інтерполяції не рівновіддалені,
, іншими словами, вузли інтерполяції не рівновіддалені,

тобто |
|
. |
Величина називається кроком |
|||
інтерполяції. |
|
|
|
|
|
|
Задача |
інтерполювання |
має |
розв‗язок, |
якщо |
степінь |
m |
багаточлена |
|
|
яким замінюється функція |
, не вище |
||
порядку  (
(  ). Тоді задача інтерполювання зводиться до пошуку невідомих
). Тоді задача інтерполювання зводиться до пошуку невідомих
постійних коефіцієнтів багаточлена |
з системи рівнянь, яка будується |
|||||
наступним чином. З початкових умов відомо, що функція |
в вузлах |
|
||||
приймає |
значення |
|
|
Тоді |
в |
вузлі |
інтерполяційний |
|
|
|
|
|
|
багаточлен |
має |
|
вигляд |
|
в |
вузлі |
інтерполяції |
- |
|
|
і так далі. Нарешті, в вузлі |
||
інтерполяційний багаточлен |
буде виглядати |
|
|
|||
|
|
|
. |
|
|
|
Запишемо |
це |
у |
вигляді |
системи |
рівнянь |
з |
невідомими |
|
|
|
|
|
|
,(5.3)
де 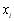 і
і  табличні значення аргументу і функції, що досліджується. Невідомі коефіцієнти
табличні значення аргументу і функції, що досліджується. Невідомі коефіцієнти  знаходяться по формулам Крамера:
знаходяться по формулам Крамера:
 , (5.4)
, (5.4)
де  - визначник системи (5.3).
- визначник системи (5.3).
Якщо  (тобто коли
(тобто коли  різні), то система (5.3) має єдиний розв‘язок.
різні), то система (5.3) має єдиний розв‘язок.
Якщо знайти коефіцієнти  , можна уявити інтерполяційний багаточлен у вигляді
, можна уявити інтерполяційний багаточлен у вигляді
Перепишемо багаточлен в іншій формі:
|
(5.5) |
Легко перевірити, що функція |
повинна задовольняти умовам |
|
|
(5.6) |
В точках |
функція |
обертається в 0, а в точці |
дорівнює 1.
Остаточно отримаємо вираз (5.7)
(5.7)

Цей багаточлен називається інтерполяційним багаточленом Лагранжа. В
спрощеному вигляді його можна записати так:
(5.8)
Даний метод легко алгоритмізується і може використовуватися для розробки програм інтерполяції. Схема алгоритму метода представлена на рисунку 5.3.
Рисунок 5.3 – Схема алгоритму метода Лагранжа
Приклад: Побудувати інтерполяційний багаточлен Лагранжа для функції заданої таблично.
n |
0 |
1 |
2 |
3 |
x |
1 |
2 |
3 |
5 |
y |
1 |
5 |
4 |
8 |
n=4; m=n-1=4-1=3. Припустимо, що y=a0+a1x+a2x2+a3x3.
Слід пам‘ятати, що при екстраполяції функції, чим далі значення х від інтервалу спостереження, тим отримане значення функції містить більшу похибку.

Таким чином: |
, |
, |
, |
. |
Висновки: |
|
|
|
|
1. Таким чином |
за допомогою багаточлена Лагранжа були отримані |
|||
коефіцієнти |
інтерполяційної |
|
функції |
|
: |
|
. |
|
|
2. Використовуючи отриманий багаточлен можливо знайти будь-яке значення
функції  для заданого
для заданого  . Наприклад, для
. Наприклад, для 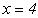

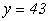 3. Використовуючи інтерполяційний багаточлен можливо отримати значення
3. Використовуючи інтерполяційний багаточлен можливо отримати значення
функції за |
межами |
спостережень. |
У |
даному |
прикладі |
інтервал |
спостереження |
|
. |
|
Така |
|
задача |
називається екстраполяція (прогнозування функції). |
|
|
||||
Для оцінки похибки інтерполяційного багаточлена Лагранжа використовують формулу:
 ,
,
причому  , при
, при 
5.2.2 Перша інтерполяційна формула Ньютона для рівновіддалених вузлів інтерполяції
Якщо функція, що досліджується, задана |
значеннями |
в рівновіддалених |
вузлах інтерполяції, |
тобто  , то для побудови її аналітичної залежності зручно використовувати першу інтерполяційну формулу Ньютона.
, то для побудови її аналітичної залежності зручно використовувати першу інтерполяційну формулу Ньютона.
Для виводу інтерполяційних формул для рівновіддалених вузлів інтерполяції вводиться поняття кінцевої різниці.
Поставимо наступну задачу: для функції  , яка задана таблицею
, яка задана таблицею
значень |
причому x змінюється |
з |
однаковим |
кроком h, тобто  , побудувати кінцеві різниці.
, побудувати кінцеві різниці.

Кінцевою різницею першого порядку  називається різність між значеннями функції в сусідніх вузлах інтерполяції:
називається різність між значеннями функції в сусідніх вузлах інтерполяції:
|
В загальному вигляді кінцеву різницю першого порядку |
можна записати |
|
як |
. |
|
|
|
Кінцева різниця другого порядку |
складається з кінцевих різниць першого |
|
порядку:
Кінцева різниця n-го порядку |
складається з кінцевих різниць |
-го |
порядку: |
|
|
 ,
,
або в технічної літературі використовують наступну формулу кінцевої різниці  -го порядку:
-го порядку:
Нехай необхідно побудувати інтерполяційний багаточлен |
|
степеню |
|||||||
такий, що |
|
|
|
|
|
|
|
|
|
|
|
Будемо |
|
шукати |
|
|
|
багаточлен |
|
виду |
|
|
|
|
|
(5.9) |
|
|
|
В цьому виразі невідомі коефіцієнти |
. |
Для |
того |
щоб |
знайти |
, |
|||
покладемо |
. |
Тоді при підстановці |
в вираз |
(5.9) |
всі |
складові, окрім |
|||
першої, обернуться в нуль, тобто |
|
а значення функції в точці |
відомі з |
||||||
умови задачі: |
Отже |
|
|
|
|
|
|
|
|
Щоб |
знайти |
коефіцієнт |
складемо першу |
кінцеву |
різницю |
для |
|||
багаточлена |
в точці x: |
|
|
|
|
|
|
|
|
Зробивши всі підстановки, отримаємо:

Обчислимо першу кінцеву різницю багаточлена в точці 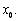 Тут також всі члени, окрім першого, обернуться в нуль, і, отже,
Тут також всі члени, окрім першого, обернуться в нуль, і, отже, 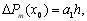 але
але
звідки |
і |
|
|
|
|
|
Щоб визначити коефіцієнт |
складаємо кінцеву різницю другого порядку: |
|
||||
Після перетворень отримаємо |
|
|
|
|
||
Вважаємо |
; тоді всі члени, окрім першого, знов обернуться в нуль |
|||||
і |
Звідси |
|
|
|
|
|
Обчислюючи |
кінцеві |
різниці |
більш високих порядків і вважаючи |
, |
||
прийдемо до загальної формули для отримання коефіцієнтів: |
|
|
||||
|
|
(5.10) |
|
|
|
|
де будемо |
вважати, |
що |
та |
Підставивши знайденні |
значення |
|
коефіцієнтів в |
вираз |
(5.9), |
отримаємо першу інтерполяційну |
формулу |
||
Ньютона. |
|
|
|
|
|
|
(5.11)
На практиці часто використовують формулу Ньютона в іншому вигляді. Для
цього введемо заміну  де
де  крок інтерполяції, а q - число кроків. Тоді перша інтерполяційна формула Ньютона прийме наступний вигляд:
крок інтерполяції, а q - число кроків. Тоді перша інтерполяційна формула Ньютона прийме наступний вигляд:
 (5.12)
(5.12)
Формулу (5.12) зручно використати для інтерполювання на початку відрізку інтерполяції  , де q мале за абсолютною величиною.
, де q мале за абсолютною величиною.
Якщо за число вузлів інтерполяції прийняти  , то отримаємо формулу лінійного інтерполювання
, то отримаємо формулу лінійного інтерполювання
При отримаємо |
формулу |
параболічного, |
або квадратичного |
інтерполювання 
На практиці часто буває необхідно зменшити крок інтерполяції якої-небудь таблиці з рівновіддаленими аргументами. В таблиці можна вважати, що кількість
вузлів інтерполяції необмежена. Тоді вибирають  так, щоб кінцева різниця
так, щоб кінцева різниця 
була постійна з заданим ступенем точності. За початкове значення  можна вибирати будь-яке значення аргументу.
можна вибирати будь-яке значення аргументу.

Схема алгоритму інтерполяції табличної функції багаточленом Ньютона представлена на рисунку 5.4.
Рисунок 5.4 – Схема алгоритму інтерполяції табличної функції багаточленом Ньютона
Приклад. Припустимо, що результати експерименту представлені в таблиці
5.2(перших три стовпця)
Зтаблиці видно, що
|
|
|
|
|
|
|
|
, |
Таблиця 5.2 – Результати експерименту |
|
|
||||||
N |
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
-1 |
3 |
12 |
6 |
|
0 |
0 |
1 |
1 |
2 |
15 |
18 |
6 |
|
0 |
|
