
125 Кібербезпека / Магістр (вступні питання)
.pdf
Доведемо перше із співвідношень.
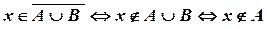 і
і 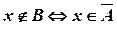 і
і 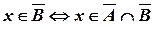 .
.
Отже, 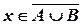
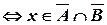 , тобто
, тобто 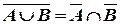 .
.
Аналогічно доводиться друге співвідношення.
Частково впорядковані множини. Нехай М − довільна множина і 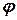 − деяке бінарне відношення в ній. Це відношення називається частковою впорядкованістю, якщо воно задовольняє умови:
− деяке бінарне відношення в ній. Це відношення називається частковою впорядкованістю, якщо воно задовольняє умови:
1)рефлексивності: 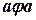 ;
;
2)транзитивності: якщо 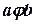 і
і 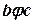 , то
, то 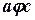 ;
;
3)антисиметричності: якщо 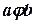 і
і  , то
, то 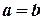 .
.
Часткова впорядкованість може позначатися символом 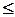 . Множина, в якій задано деяку часткову впорядкованість, називається частково впорядкованою. Запис
. Множина, в якій задано деяку часткову впорядкованість, називається частково впорядкованою. Запис 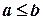 означає, що елемент а не перевищує b або що він підпорядкований b, передує b, а b −не менше від а йде за а.
означає, що елемент а не перевищує b або що він підпорядкований b, передує b, а b −не менше від а йде за а.
У випадку, коли |
та |
, користуються символом < , тобто |
пишуть 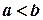 і говорять, що а менше від b або що а строго підпорядковане b. Частково впорядкована множина, для будь-яких двох точок а, b якої
і говорять, що а менше від b або що а строго підпорядковане b. Частково впорядкована множина, для будь-яких двох точок а, b якої
існує точка c, що йде за ними ( 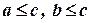 ), називається напрямленою.
), називається напрямленою.
87. Відношення. Основні види відношень. Бінарні відношення, способи їх задання, основні властивості
Відношення (від англійського relation — відношення) — фундаментальне поняття реляційної моделі даних. З цієї причини модель і називається реляційною.
Відношення в реляційному моделюванні — набір кортежів, інакше відомий як таблиця бази даних.
Поняття відношення покладено в основу реляційних моделей, яке подають у вигляді двовимірної таблиці. Реляційна БД — це набір взаємопов‘язаних відношень. Кожне відношення (таблиця) в ЕОМ подається як файл. Відношення можна поділити на два класи: об‘єктні і зв‘язкові.
Об'єктні відношення Об’єктні відношення зберігають дані про інформаційні об‘єкти
предметної області. Наприклад: клієнт (код клієнта, назва клієнта, адреса, телефон) є об‘єктним відношенням. В об‘єктному відношенні один з атрибутів однозначно ідентифікує окремий об‘єкт. Такий атрибут називається первинним ключем відношення. В наведеному відношенні роль ключа виконує атрибут «код клієнта». Ключ може вмикати кілька атрибутів, тобто бути складеним. В об‘єктному відношенні не повинно бути рядків з однаковим ключем, тобто не допускається дублювання об‘єктів. Це основне обмеження реляційної моделі для забезпечення цілісності даних.
Зв'язкове відношення
Зв’язкове відношення зберігає ключі двох або більше об‘єктних відношень. Ключі зв‘язкового відношення мають на меті встановлення зв‘язків між об‘єктними відношеннями. Наприклад, розглянемо ще одне об‘єктне відношення БАНК(код банку, назва банку, адреса банку). Тоді зв‘язкове відношення БАНК-КЛІЄНТ (код банку, код клієнта) буде сполучним між двома об‘єктними відношеннями БАНК іКЛІЄНТ. У зв‘язковому відношенні можуть дублюватися ключові атрибути. Крім ключів, за якими встановлюють зв‘язок у зв‘язковому відношенні, можуть бути ще й інші атрибути, які функціонально залежать від цього складового ключа. Ключі в зв‘язкових відношеннях називаються зовнішніми ключами, оскільки вони є первинними ключами інших відношень. Реляційна модель накладає на зовнішні ключі обмеження, яке називають посилковою цілісністю. Воно необхідне для забезпечення цілісності даних. Це означає, що кожному зовнішньому ключеві має відповідати рядок якогось об‘єктного відношення. Без такого обмеження може статися так, що зовнішній ключ посилається на об‘єкт, про який нічого не відомо.
У реляційній БД накладається ще одне обмеження — відношення мають бути нормалізовані.
Види відношень
1.Рефлексивне транзитивне відношення називається відношенням квазіпорядка.
2.Рефлексивне симетричне транзитивне відношення називається відношенням еквівалентності
3.Рефлексивне антисиметричне транзитивне відношення називається відношенням (часткового) порядку.
4.Антирефлексивне антисиметричне транзитивне відношення називається відношенням строгого порядку.
5.Повне антисиметричне транзитивне відношення називається відношенням лінійного порядку.
6.Антирефлексивне асиметричне відношення називається відношенням домінування.
Бінарні відношення – теоретичне підґрунтя теорії прийняття рішень, оскільки для дослідження переваг децидента використовують основні типи бінарних відношень, а властивості бінарних відношень інтерпретуються якісно
втермінах системи переваг децидента. Доведені твердження дають можливість побудувати алгоритми перевірки експериментальних відношень на наявність таких важливих властивостей, як транзитивність, ациклічність, лінійність, щоб виявляти і корегувати суперечності в міркуваннях децидента.
Апарат бінарних відношень у теорії прийняття рішень є теоретичним підґрунтям для оцінювання переваг альтернатив шляхом попарних порівнянь. Такий підхід достатньо поширений, оскільки він дає змогу виявляти переваги децидента чи експертів «у чистому вигляді»: децидентові значно простіше порівняти дві альтернативи, ніж багато.
Способи задання бінариних відношень
Якщо R – бінарне відношення на множинах X, Y, то факт 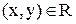 часто записують у вигляді xRy, і кажуть, що елемент x перебуває у відношенні
часто записують у вигляді xRy, і кажуть, що елемент x перебуває у відношенні
R з елементом 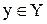 .
.
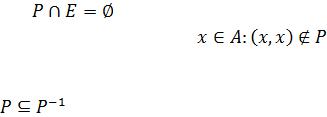
Будь-яке бінарне відношення може бути задано у вигляді списку, елементами якого є пари, з яких складається відношення.
Бінарне відношення R на множинах X і Y може бути задано за допомогою матриці (W=W(R)), рядки якої відповідають елементам множини Х,
стовпці – елементам множини Y. Якщо 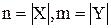 – кількість елементів множин Х і Y відповідно, то матриця W має розмірність
– кількість елементів множин Х і Y відповідно, то матриця W має розмірність 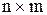 . Елемент
. Елемент 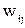 матриці W відповідає парі
матриці W відповідає парі 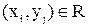 , при цьому
, при цьому 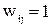 , якщо
, якщо 
і 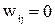 , якщо
, якщо 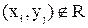 .
.
Бінарне відношення R на множинах X, Y може бути задано графічно. На площині точками 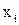 та
та  зображуються елементи множин Х і Y. Якщо
зображуються елементи множин Х і Y. Якщо
пара 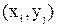 належить відношенню R, точки
належить відношенню R, точки 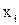 та
та 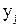 з'єднуються стрілкою (дугою), спрямованою від першого елемента пари до другого. Позначивши таким чином всі пари, що належать відношенню R, отримується фігура, яка називається графом відношення. Стрілки, що з'єднують пари точок, називаються дугами, а точки, що зображують елементи множин, – вершинами графа.
з'єднуються стрілкою (дугою), спрямованою від першого елемента пари до другого. Позначивши таким чином всі пари, що належать відношенню R, отримується фігура, яка називається графом відношення. Стрілки, що з'єднують пари точок, називаються дугами, а точки, що зображують елементи множин, – вершинами графа.
Властивості та основні типи бінарних відношень
У теорії прийняття рішень використовують певні типи бінарних відношень із конкретними властивостями. Один із підходів полягає у формулюванні властивостей бажаного відношення у формі аксіом із подальшим пошуком конструктивного методу побудови такого відношення чи класу відношень або ж доведення неможливості його існування, якщо сформульована система аксіом суперечлива [25].
Основні властивості відношень –
рефлексивність, антирефлексивність, симетричність, асиметричність, антис иметричність, транзитивність і ациклічність.
ОЗНАЧЕННЯ 2.22. Рефлексивним називається таке відношення Р, для якого справедливе твердження Е Í Р, де Е – діагональне відношення.
Це означає, що для всіх хÎА, де А – носій відношення Р, хРх. У матриці рефлексивного відношення на головній діагоналі завжди стоять 1, а у відповідному графі при кожній вершині є петля.
ОЗНАЧЕННЯ 2.23. Антирефлексивним називається відношення Р,
для якого |
. |
|
|
|
|
Таким чином, для всіх |
, тобто в матриці відношення на |
||||
головній діагоналі завжди стоять 0, а в графі – немає петель. |
|
||||
ОЗНАЧЕННЯ |
2.24. |
Симетричним називається відношення Р, для |
|||
якого |
. |
|
|
|
|
Для |
всіх х, yÎА, |
які |
перебувають у такому відношенні Р, |
тобто хРу, |
|
справедливе |
твердження уРх. У |
матриці симетричного |
відношення |
||
елементи bij та bji розміщені симетрично відносно головної діагоналі, рівні між собою. У графі G(P) наявність дуги (xi, xj) означає, що є і дуги (хj, хi).

ОЗНАЧЕННЯ 2.25. Асиметричним називається відношення Р, для якого 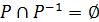 , тобто якщо
, тобто якщо 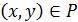 , то
, то 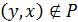 .
.
У матриці такого відношення 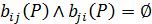 для всіх і та j, а на головній діагоналі знаходяться 0. У графі G(P) немає водночас дуг (хi, хj) та (xj, хi), а також петель.
для всіх і та j, а на головній діагоналі знаходяться 0. У графі G(P) немає водночас дуг (хi, хj) та (xj, хi), а також петель.
ОЗНАЧЕННЯ 2.26. Антисиметричним називається |
відношення Р, |
|
якщо |
, де Е – діагональне відношення. |
|
Отже, |
твердження хРу та уРх справедливі водночас |
лише тоді, |
коли х = у. У матриці В(Р) умова 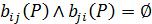 виконується для всіх і, j, окрім і = j. У графі G(P) немає водночас дуг (хi, хj) та (xj, хi), але можуть бути петлі.
виконується для всіх і, j, окрім і = j. У графі G(P) немає водночас дуг (хi, хj) та (xj, хi), але можуть бути петлі.
Интернет реклама УБС
Приклад 2.20. Розглянемо відношення Р, Q, R:
Відношення P симетричне та рефлексивне, Q – антирефлексивне і асиметричне, R – антисиметричне, що перевіряється безпосередньо за означеннями цих властивостей:
Приклад 2.21. Розглянемо приклади відношень із наведеними вище властивостями.
Відношення між об‘єктами «бути подібним», «бути не молодшим»
рефлексивні, тому що об‘єкт подібний на самого себе (тотожний сам собі), людина не молодша за саму себе.
Відношення «відрізнятися», «бути молодшим», «бути батьком» не рефлексивні. Більше того, вони антирефлексивні (тому що об‘єкт не може відрізнятися від самого себе, бути молодшим за самого себе чи бути батьком самому собі).
Відношення «бути родичем» симетричне (якщо А – родич В, то і В – родич А), «бути батьком» – асиметричне (якщо А – батько В, то В не батько А).

Відношення «бути сестрою» не симетричне і не асиметричне. Так, якщо Марія – сестра Ольги, то Ольга – сестра Марії, але якщо Марія – сестра Петра, то, звичайно ж, Петро – не сестра Марії.
|
Відношення «³» на множині дійсних чисел антисиметричне. |
|
ОЗНАЧЕННЯ 2.27. Транзитивним називається відношення, для |
якого |
, тобто якщо xPz і zPy, то хРу. |
|
За індукцією як наслідок отримуємо: якщо xPz1, z1Pz2, ..., znPy, то хРу. У |
матриці В(Р) транзитивного відношення для довільних значень і, k виконується співвідношення
У графі G(P) транзитивного відношення Р якщо існує шлях з x в у, то існує дуга (х, у).
Із поняттям транзитивного відношення тісно пов‘язане поняття операції
транзитивного замикання. Для кожного відношення Р означимо відношення 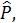 як мінімальне транзитивне відношення, у якому міститься відношення Р. Його
як мінімальне транзитивне відношення, у якому міститься відношення Р. Його
однозначно означають як  , де n = саrd(A), А – носій відношення Р, a card(A) – потужність множини А.
, де n = саrd(A), А – носій відношення Р, a card(A) – потужність множини А.
Приклад 2.22. Знайдемо транзитивне замикання відношення
.
,
,
ОЗНАЧЕННЯ |
2.28. Ациклічним називається відношення Р, |
для |
||
якого |
для довільного k. |
|
|
|
Для ациклічного відношення з xPz1, z1Pz2, |
..., znPy випливає х ¹ у, |
тобто |
||
якщо в графі G(P) |
ациклічного відношення Р вершини х та у з‘єднані шляхом, |
|||
то в ньому немає дуги (у, х). |
|
|
||
Ациклічність і |
транзитивність – важливі |
властивості для ТПР, |
вони |
|
відображають певні природні взаємозв‘язки між об‘єктами. Якщо об‘єкт х у
певному розумінні кращий |
за у, |
а укращий за z, то природно вважати, що |
|||
об‘єкт х кращий, ніж z (транзитивність), |
і |
щонайменше |
об‘єкт z не кращий |
||
за х (ациклічність). |
|
|
|
|
|
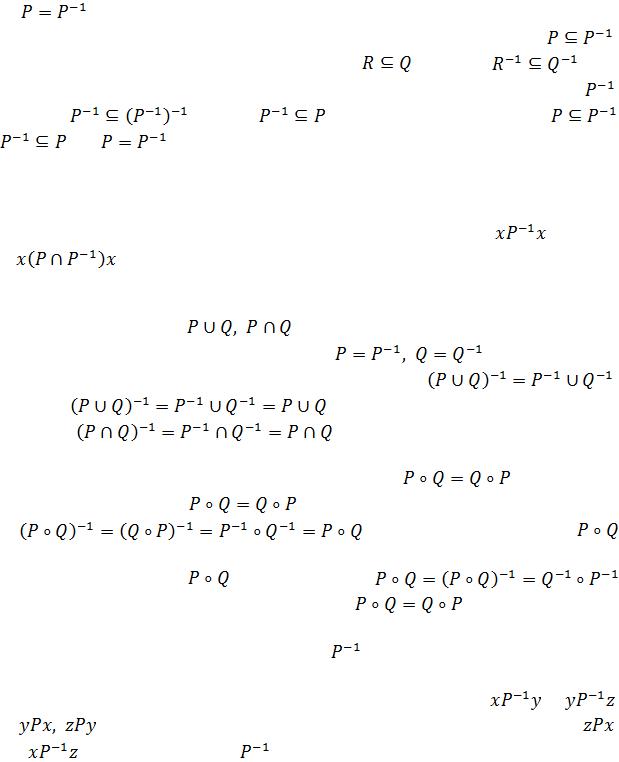
ОЗНАЧЕННЯ 2.29. Зв’язним відношенням називається відношення Р, |
|||||
для якого |
, |
де |
– |
обернене |
до Р відношення, U – |
повне, Е – діагональне. |
|
|
|
|
|
|
Це |
означає, |
що |
для |
довільних |
елементів х, у Î А, х ¹ у, |
де А – |
носій |
|||||||||||||
відношення Р, чи |
(х,у) |
Î Р, |
чи (у, х) |
Î Р. |
У |
матриці В(Р) |
хоча |
б один |
з |
||||||||||||
елементів bij, bji |
дорівнює 1, а граф G(P) зв‘язний. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Доведемо декілька тверджень, які стосуються взаємозв‘язків між |
||||||||||||||||||||
властивостями відношень. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ТВЕРДЖЕННЯ |
2.1. Відношення Р симетричне |
тоді |
й |
лише |
|
тоді, |
||||||||||||||
коли |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доведення. За означенням для симетричного відношення |
|
|
. |
|||||||||||||||||
Оскільки |
для |
довільних відношень R і Q з |
|
випливає |
|
|
|
|
, |
то |
|||||||||||
підставивши |
|
замість R відношення Р, |
|
|
а |
|
|
|
замість Q – |
|
, |
||||||||||
отримаємо |
|
|
|
, |
або |
|
. |
|
Оскільки |
|
водночас |
|
|
|
|||||||
та |
|
, то |
|
. ¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ТВЕРДЖЕННЯ |
2.2. Якщо |
відношення Р асиметричне, |
то |
|
воно |
|||||||||||||||
антирефлексивне. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Доведення. Нехай для хÎА, де А – носій відношення Р, виконується хРх. |
||||||||||||||||||||
За |
означенням |
оберненого |
відношення |
це означає, |
що |
|
|
. |
Однак |
||||||||||||
тоді |
|
, |
що |
суперечить |
припущенню |
про |
|
асиметричність |
|||||||||||||
відношення Р. ¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ТВЕРДЖЕННЯ |
2.3. Якщо |
|
відношення Р та Q симетричні, |
|
|
то |
||||||||||||||
симетричні й відношення |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Доведення. За твердженням 2.1, |
|
|
|
|
|
. |
Виходячи |
з |
||||||||||||
справедливості |
|
|
|
|
співвідношення |
|
|
|
|
|
|
|
|
, |
|||||||
отримаємо |
|
|
|
|
|
|
|
, |
що |
і |
доводить |
твердження. |
|||||||||
Аналогічно |
|
|
|
|
|
|
. ¨ |
|
|
|
|
|
|
|
|
|
|
|
|||
|
ТВЕРДЖЕННЯ |
|
|
2.4. Композиція |
|
|
|
|
симетричних |
||||||||||||
відношень Р та Q симетрична тоді й лише тоді, коли |
|
|
|
|
|
. |
|
|
|
|
|||||||||||
|
Доведення. Нехай |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тоді |
|
|
|
|
|
|
|
|
|
, |
тобто |
|
композиція |
|
|
||||||
симетрична, що доводить достатність умови комутативності. |
|
|
|
|
|
|
|
||||||||||||||
|
Нехай відношення |
|
симетричне. Тоді |
|
|
|
|
|
|
|
|
|
|
||||||||
. |
Позаяк |
відношення Р та Q симетричні, |
то |
|
|
|
, |
що |
й |
доводить |
|||||||||||
необхідність умови комутативності. ¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ТВЕРДЖЕННЯ |
2.5. Відношення |
|
обернене |
до |
транзитивного |
|||||||||||||||
відношення Р, є транзитивним. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Доведення. Нехай Р – |
|
транзитивне |
відношення, |
й |
|
|
та |
|
|
. |
||||||||||
Тоді |
, |
і |
внаслідок |
|
того, що Р – |
транзитивне |
відношення, |
|
, |
||||||||||||
тобто |
. Отже, відношення |
транзитивне. ¨ |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
ТВЕРДЖЕННЯ |
2.6. Перетин |
довільної |
кількості |
|
транзитивних |
|||||||||||||||
відношень з одним і тим самим носієм є транзитивним відношенням. |
|
|
|
|
|||||||||||||||||
|
Доведення. Розглянемо множину транзитивних відношень {Рi}, iÎІ, з |
||||||||||||||||||||
носієм А. |
|
Нехай хРу, yPz. |
Це |
|
означає, |
|
|
|
що |
|
|
для |
|||||||||
довільного iÎІ виконується хРiу, yPiz.
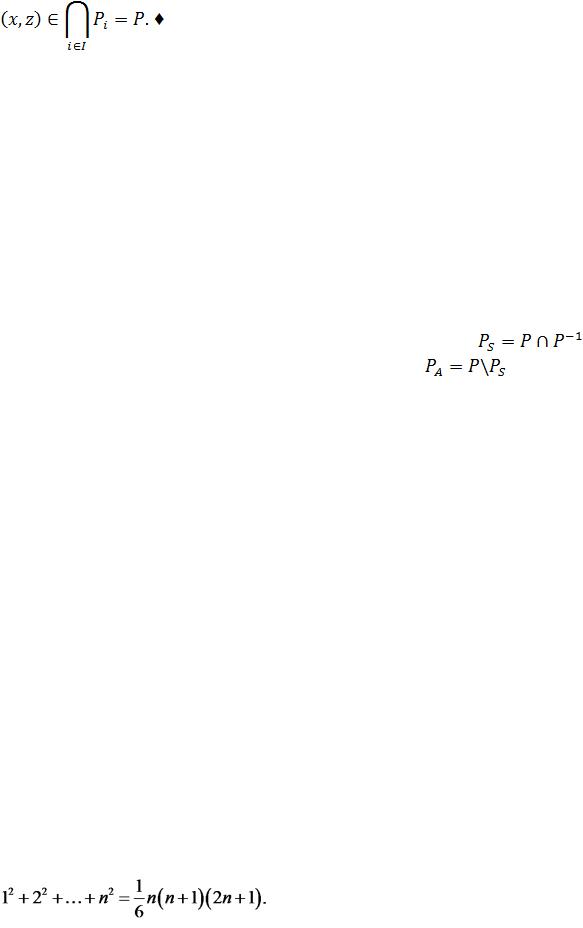
Оскільки відношення Рi транзитивне, то хРiz. Оскільки хРiz виконується для довільного iÎІ, це означає, що
Для операції об‘єднання подібне твердження неправильне. Це має глибокий прикладний сенс: якщо ми хочемо побудувати результуюче групове відношення, за умови транзитивності відношення кожного з експертів, то після об‘єднання властивість транзитивності результуючого відношення зникає.
Результуюче відношення, отримане об‘єднанням транзитивних відношень, також транзитивне, якщо виконуються деякі додаткові умови. Уведемо поняття транзитивності одного відношення щодо іншого. Відношення Р називатимемо транзитивним стосовно відношення Q, якщо з хРуÙyQz випливає xPz, а з xQyÙyPz — xPz.
Неважко довести твердження 2.7 і 2.8, що визначають умови транзитивності.
ТВЕРДЖЕННЯ 2.7. Якщо два відношення транзитивні й одне з них
транзитивне відносно іншого, то об‘єднання цих відношень транзитивне. |
|
||||
Нехай Р — довільне |
бінарне відношення. Відношення |
|
|
||
називається симетричною |
складовою відношення Р, а |
— |
його |
||
асиметричною складовою. |
|
|
|
|
|
ТВЕРДЖЕННЯ 2.8. Нехай Р – транзитивне відношення. |
Тоді |
його |
|||
симетрична |
складова PS і |
асиметрична |
складова РА транзитивні. |
А |
|
відношення РА транзитивне відносно PS. |
|
|
|
||
88. Метод математичної індукції. Формула включень та виключень
Метод математичної індукції:
1. Перевіряємо, що деяке твердження справджується для початкового
номеру 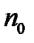 (база індукції).
(база індукції).
2. Припускаємо, що це твердження вірне або для деякого номера 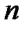 ,
,
або для всіх натуральних чисел, починаючи з 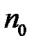 , які не перевищують
, які не перевищують 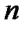 (припущення індукції).
(припущення індукції).
3. Аналізуючи припущення індукції, доводимо, що наше твердження
вірне й для наступного номера 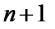 (індукційний крок).
(індукційний крок).
4. Робимо висновок, що дане твердження вірне для всіх натуральних
чисел, починаючи з 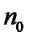 .
.
Приклад 1. Методом математичної індукції довести, що для всіх натуральних чисел має місце рівність
Доведення.
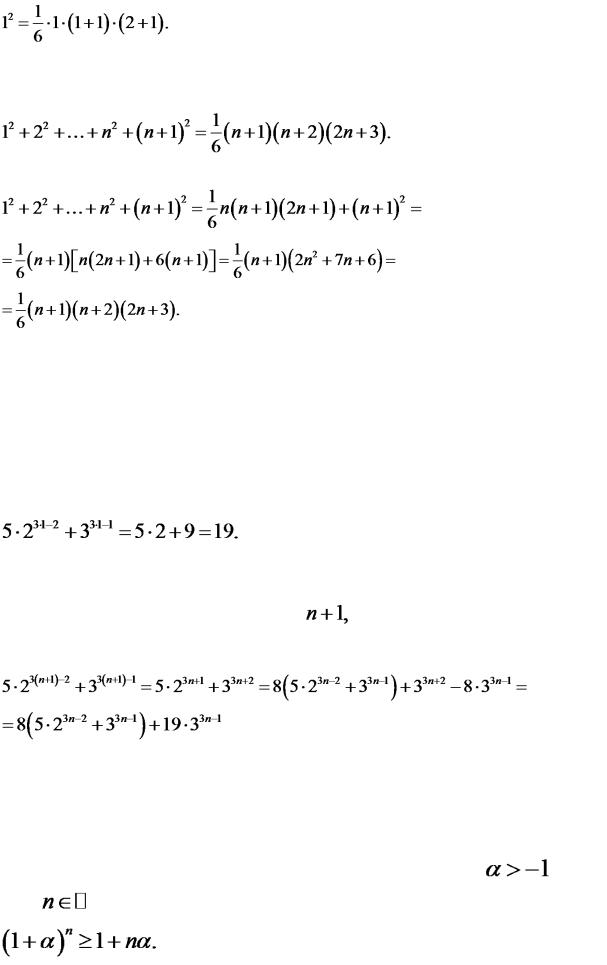
1.Рівність вірна при 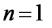 . Дійсно,
. Дійсно,
2.Припустимо, що рівність виконується для деякого натурального 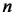 .
.
3.Доведемо рівність для  , тобто
, тобто
Дійсно,
Згідно з принципом математичної індукції рівність виконується для всіх
натуральних чисел. 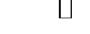 Приклад 2. Довести методом математичної індукції, що
Приклад 2. Довести методом математичної індукції, що
число 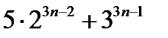 ділиться на 19 для будь-якого
ділиться на 19 для будь-якого 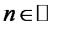 . Доведення.
. Доведення.
1.Твердженя вірне при 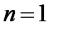 . Дійсно,
. Дійсно,
2.Припустимо, що твердження виконується для деякого натурального 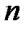 .
.
3. Доведемо твердження для |
тобто перевіримо, що |
вираз 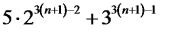 ділиться на 19. Дійсно,
ділиться на 19. Дійсно,
Перший доданок ділиться на 19 за припущеннням, другий доданок теж
ділиться на 19. Отже твердження має місце для 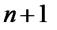 .
.
За принципом математичної індукції твердження виконується для всіх натуральних чисел. 
Приклад 3 (нерівність Бернуллі). Довести, що при |
та |
довільному

Доведення.
1.Нерівність справджується при 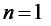 . Дійсно,
. Дійсно,
2.Припустимо, що нерівність виконується для деякого натурального
.
3. Доведемо нерівність для 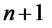 , тобто
, тобто
Таким чином, нерівність доведена для всіх натуральних чисел.
Формула включень та виключень
Розглянемо формулу решта, яка має застосування в теорії ймовірностей і ілюструється за допомогою діаграм Ейлера-Венна.
Нехай 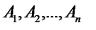 – підмножини множини
– підмножини множини 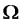 .
.
Нехай 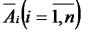 – доповнення до цих множин.
– доповнення до цих множин.
Позначимо 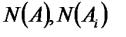 ,
, 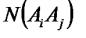 ,
,
..., 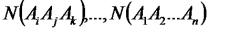 ,
,
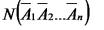 ,
, 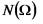 – число елементів відповідних множин. Має місце формула:
– число елементів відповідних множин. Має місце формула:
.
Якщо, зокрема, мова йде про три підмножини  (скажімо,
(скажімо, 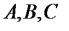 ), то одержуємо формулу:
), то одержуємо формулу:
. (*)
Наприклад. Із 90 випускників вузу 50 знають англійську мову, 30 – німецьку і 20 – французьку. Англійську і німецьку мову знають 10 випускників, англійську і французьку – 8, німецьку і французьку – 5, всі 3 мови – 3 випускники. Скільки випускників не знають жодної з цих мов?
Розв'язок. Позначимо через А множину випускників, що знають
англійську мову, через В – німецьку, через С – французьку. Нехай 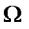 – множина усіх 90 випускників.
– множина усіх 90 випускників.
За формулою (*) одержуємо:
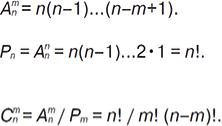
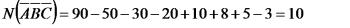 .
.
Таким чином, 10 випускників не знають жодної з цих мов.
Цей же самий приклад можна розв‘язати за допомогою діаграм Ейлера-
Венн
89. Елементи комбінаторного аналізу. Правила суми та добутку. Комбінації з повтореннями та без повторень
КОМБІНАТО́РНИЙ АНА́ЛІЗ – розділ математики, присвячений вирішенню завдань вибору та розміщення елементів деякої, зазвичай скінченної множини відповідно до заданих правил. Результат такого вибору називають комбінатор. конфігурацією. Метою К. а. є вивчення комбінатор. конфігурацій, алгоритмів їхньої побудови, оптимізації таких алгоритмів, а також визначення кількості конфігурацій певного класу. Гол. частину К. а. становлять методи безпосеред. підрахунку кількості конфігурацій, метод твір. функцій, логічні, екстремал., геом. та ін. методи. При підрахунку кількості комбінатор. конфігурацій важливу роль відіграє правило множення (осн. принцип К. а.): якщо дію А можна здійснити m способами, а дію B – n способами, то заг. кількість усіх способів послідов. здійснення дій A і B дорівнює m • n. Найпростішими прикладами комбінатор. конфігурацій є розміщення, перестановки, комбінації. Якщо з множини M, що складається з n елементів, послідовно по одному вибирають m елементів, то одержані набори (відрізняються один від одного або елементами, або їхнім порядком) називають розміщеннями з n елементів по m. Кількість таких розміщень
Розміщення з n елементів по n називають перестановками. Їхня кількість
Комбінації з n елементів по m – це всі можливі m-елементні підмножини з M; їхня кількість
Багато комбінаторних задач можуть бути розв‘язані за допомогою двох важливих правил, які називають відповідно правило суми і правило добутку.
Спочатку розглянемо правило суми:
якщо деякий елемент А можна вибрати m способами, а елемент В — r способами (причому будь-який вибір елемента А відрізняється від вибору елемента В), то вибрати А або В можна m + r способами.
Дышите свободно в своей машине!m грн.Универсальная точилка "Swifty Sharp"m грн.Нарезайте овощи быстро и удобноh грн.
Приклад 1. В ящику знаходиться 7 білих і 4 чорних кульки. Тоді вибрати одну кульку: білу або чорну можна 7 + 4 = 11 способами.
Зрозуміло, що правило суми можна розповсюдити на три і більше елементів.
Сформулюємо правило добутку:
