
125 Кібербезпека / Магістр (вступні питання)
.pdf
101. Випадкові процеси. Кореляційна теорія випадкових процесів.
Характеристики суми випадкових процесів
Теорією випадкових процесів (в. п.) називається математична наука, яка вивчає закономірності випадкових явищ в динаміці їх розвитку. Випадкові процеси описують багато фізичних, економічних та виробничих явищ. До них належать броунівський рух дрібної частинки, який виникає внаслідок взаємодії частинки з молекулами рідини, коливання валютних курсів, курсів акцій, ціни на певний товар, сподівана вартість грошей, банківські активи, довжина черг та кількість заявок на обслуговування в кожний момент часу з деякого проміжку часу в різних системах надання послуг тощо.
Поняття випадкового процесу є узагальненням поняття випадкової величини.
Розглянемо деяку числову множину  , елементи якої позначатимемо через
, елементи якої позначатимемо через  і будемо вважати їх моментами часу.
і будемо вважати їх моментами часу.
Означення. Випадковим процесом називається функція  ,
,  ,
,
значення якої при будь-якому фіксованому  є випадковою величиною
є випадковою величиною  .
.
Випадкову величину  , в яку перетворюється випадковий процес при
, в яку перетворюється випадковий процес при  , називається перерізом випадкового процесу, що відповідає даному значенню аргумента
, називається перерізом випадкового процесу, що відповідає даному значенню аргумента  . Надалі, розглядаючи переріз випадкового процесу, ми не завжди відзначатимемо нульовим індексом те значення аргумента
. Надалі, розглядаючи переріз випадкового процесу, ми не завжди відзначатимемо нульовим індексом те значення аргумента  , якому
, якому
воно відповідає, а будемо інтерпретувати один і той же вираз  або як випадковий процес (при змінному
або як випадковий процес (при змінному  ), або як випадкову величину (при фіксованому
), або як випадкову величину (при фіксованому  ).
).
Якщо розглянути не один переріз випадкового процесу, а ряд перерізів в
точках |
, |
то |
отримаємо -вимірний |
випадковий |
|
вектор |
|
, який описує випадковий процес лише |
в |
||
деякому |
наближенні. |
Сукупність |
всіх перерізів при |
всеможливих і |
є |
випадковий процес  . Отже, випадковий процес представляє не що інше, як сім‘ю випадкових величин – всіх перерізів цього процесу.
. Отже, випадковий процес представляє не що інше, як сім‘ю випадкових величин – всіх перерізів цього процесу.

Аналогічно до того, як ми записували випадкову величину у вигляді функції від елементарної події, яка є результатом досліду (стохастичного експерименту), можна і випадковий процес записати у вигляді функції від двох аргументів – часу  та елементарної події
та елементарної події  :
:
 , (1)
, (1)
де  – елементарна подія,
– елементарна подія,  – простір елементарних подій,
– простір елементарних подій,  – область
– область
(множина) значень аргумента  функції
функції  .
.
Якщо  – фіксоване, то
– фіксоване, то  , що розглядається як функція
, що розглядається як функція
,  , називається реалізацією або траєкторією випадкового процесу
, називається реалізацією або траєкторією випадкового процесу  .
.
Означення. Реалізацією |
випадкового |
процесу |
називається |
невипадкова функція  , в яку перетворюється випадковий процес
, в яку перетворюється випадковий процес  внаслідок проведеного досліду.
внаслідок проведеного досліду.
Користуючись формулою (1), для 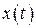 можна записати рівність
можна записати рівність
 . (2)
. (2)
Якщо здійснити не один дослід, а декілька, внаслідок кожного з яких спостерігається реалізація випадкового процесу  (
( – номер досліду), то отримаємо декілька реалізацій випадкового процесу:
– номер досліду), то отримаємо декілька реалізацій випадкового процесу:  (
(  –
–
кількість проведених дослідів) або сім‘ю реалізацій.
Сім‘я реалізацій випадкового процесу – основний емпіричний матеріал,
на підставі якого можна оцінити характеристики випадкового процесу (про них йтиме мова в наступному підрозділі). Сім‘я реалізацій випадкового процесу аналогічна сукупності спостережуваних значень випадкової величини  , з
, з
тією різницею, що тут спостерігаються не числові значення, а функції.
Далі нам доведеться мати справу із системами різноманітної природи,
зокрема, з економічними та фінансовими. Випадковий процес, який відбувається у системі  , полягає в тому, що з плином часу
, полягає в тому, що з плином часу  система
система  у випадковий спосіб змінює свій стан. Якщо система
у випадковий спосіб змінює свій стан. Якщо система  в момент
в момент  описується
описується

однією |
скалярною |
випадковою величиною |
, то |
ми маємо |
справу зі |
|||
скалярним випадковим |
процесом |
. Якщо |
стан |
системи в |
момент |
|||
описується декількома випадковими величинами |
|
|
|
, то ми |
||||
маємо |
справу |
з |
векторним |
випадковим |
процесом |
з |
||
складовими: |
|
. |
|
|
|
|
|
|
|
В теорії випадкових процесів прийнято класифікувати їх за тими або |
|||||||
іншими ознаками, враховуючи плавність або стрибкоподібність реалізації,
фіксованість або випадковість моментів, в які можуть відбуватися стрибки,
вигляд закону розподілу окремого перерізу або сукупності його перерізів і т. д.
Ознайомимося з найелементарнішою класифікацією випадкових процесів – «за часом» і «за станами».
Означення. Випадковий процес  називається процесом з дискретним часом, якщо система
називається процесом з дискретним часом, якщо система  , в якій він відбувається, може змінювати
, в якій він відбувається, може змінювати
свої стани тільки у визначені, наперед відомі моменти часу |
, які |
називаються кроками (або етапами) цього процесу. Множина |
є скінченною |
або зліченною. |
|
У проміжках часу між сусідніми кроками система зберігає свої стани. Не
виключається можливість, що на деяких кроках система не змінить свого стану.
Випадковий процес з дискретним часом називається також випадковою послідовністю. Якщо стан системи  описується одною випадковою величиною
описується одною випадковою величиною  , то випадковий процес представляє послідовність випадкових
, то випадковий процес представляє послідовність випадкових
величин |
. В |
якості аргумента |
послідовності |
можна |
|
вибрати значення номера моменту переходу |
|
. Тоді випадковий |
|||
процес можна представити |
у |
вигляді |
послідовності випадкових |
||
величин |
. |
|
|
|
|
Означення. Випадковий |
прогрес |
називається процесом |
з |
||
неперервним часом, якщо система |
, в |
якій він |
відбувається, |
може |
|
змінювати свої стани в будь-які, випадкові моменти часу, що неперервно заповнюють вісь 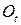 (або її ділянку). Множина
(або її ділянку). Множина  є нескінченною та незліченною.
є нескінченною та незліченною.
Означення. Випадковий процес  , який відбувається в системі
, який відбувається в системі  ,
,
називається процесом з дискретними станами, якщо в будь-який момент часу  множина його станів є скінченною або зліченною; іншими словами, якщо його переріз в будь-який момент
множина його станів є скінченною або зліченною; іншими словами, якщо його переріз в будь-який момент  характеризується дискретною випадковою
характеризується дискретною випадковою
величиною  – в одновимірному випадку та векторною дискретною
– в одновимірному випадку та векторною дискретною
випадковою величиною 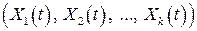 – в багатовимірному випадку.
– в багатовимірному випадку.
Зауважимо, що всі випадкові процеси з «якісними» станами відносяться до категорії процесів з дискретними станами; перерізом такого процесу є випадкова подія – аналог дискретної випадкової величини.
Означення. Випадковий процес, який відбувається в системі  ,
,
називається процесом з неперервними станами, якщо множина можливих станів системи  незліченна; іншими словами, якщо переріз процесу в будь-
незліченна; іншими словами, якщо переріз процесу в будь-
який момент часу  характеризується неперервною (або змішаною)
характеризується неперервною (або змішаною)
випадковою величиною – в одновимірному випадку та векторною неперервною
(або змішаною) випадковою величиною – в багатовимірному випадку.
За вищевказаними ознаками випадкові процеси можна поділити на чотири класи:
А1. Процеси з дискретними станами та дискретним часом.
А2. Процеси з дискретними станами та неперервним часом.
Б1. Процеси з неперервними станами та дискретним часом.
Б2. Процеси з неперервними станами та неперервним часом.
Приклад процесу типу А1: Особа купила  білетів виграшного займу,
білетів виграшного займу,
які можуть вигравати та погашатися в завчасно відомі моменти часу
(тиражі)  . Випадковий процес
. Випадковий процес  – число білетів, на які припав виграш до моменту
– число білетів, на які припав виграш до моменту  .
.

Приклад процесу типу А2: технічний прилад складається з  вузлів, які можуть в ході роботи приладу відмовляти (виходити з ладу). Випадковий
вузлів, які можуть в ході роботи приладу відмовляти (виходити з ладу). Випадковий
процес  – кількість вузлів, що відмовили до моменту
– кількість вузлів, що відмовили до моменту 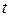 .
.
Приклад процесу типу Б1: у певні моменти часу |
реєструється |
температура повітря  у заданій точці простору. Послідовність значень цієї
у заданій точці простору. Послідовність значень цієї
величини – випадковий процес  з неперервними станами та дискретним часом.
з неперервними станами та дискретним часом.
Приклад процесу типу Б2: у мікроскоп протягом проміжку часу  спостерігається переміщення малої частинки в рідині, яка здійснює
спостерігається переміщення малої частинки в рідині, яка здійснює
броунівський рух. Координата частинки в момент  – випадковий процес
– випадковий процес  з неперервними станами та неперервним часом.
з неперервними станами та неперервним часом.
102. Гармонійні, полігармонійні, перехідні процеси. Стаціонарні
процеси
В залежності від мети, яка ставиться при обробці даних, можна виділити дві задачі:
Аналіз даних отриманих шляхом спостережень фізичних процесів, які мають місце у досліджуваному об’єкті з метою вивчення властивостей цього об’єкту.
Моделювання фізичних процесів, які мають місце у досліджуваному об’єкті з метою розробки методів для оцінки та прогнозування зміни властивостей цього об’єкту в залежності від впливу зовнішніх та внутрішніх факторів.
Вибір методів збору та обробки даних спостережень випадкових процесів значною мірою залежить від того, яке фізичне явище являє досліджуваний фізичний процес, та від мети, якої слід досягти в результаті обробки. У загальному випадку можна виділити п’ять основних етапів цієї процедури:
Збір данихРеєстрація та передача даних
Попередня підготовка данихОцінювання основних властивостей даних
Аналіз даних (статистичний, кореляційний, спектральний)
Досить часто моделювання фізичних процесів дає швидші результати ніж їх спостереження. Крім того під час моделювання є можливість досліджувати впливаючі величини та змінювати параметри процесу, які відображають стан реального фізичного об’єкта. При такому моделюванні слід враховувати структуру фізичного процесу, в якій можуть бути наявні як детерміновані так і випадкові складові в залежності від природи процесу (рисунок 1.1).

Рисунок 1.1 Види фізичних процесів в залежності від їх природи
Детерміновані – процеси, миттєві значення і параметри яких відомі у будьякий момент часу з ймовірністю рівній одиниці. Тобто часову залежність миттєвих значень і параметрів таких сигналів можна задати математичним описом (формулою).
Періодичні – процеси, миттєві значення яких повторюються через однакові інтервали часу:
 ,
, 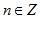 ,
, 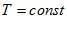 .
.
Гармонічні – періодичні процеси, поведінка миттєвих значень яких описується гармонічною залежністю:
Полігармонічні - періодичні процеси, поведінка миттєвих значень яких описується сумою декількох гармонійних залежностей, відношення будь-яких частот яких є раціональним числом.
Неперіодичні - процеси, миттєві значення яких не повторюються через однакові інтервали часу.
Майже періодичні – полігармонічні процеси, відношення будь-яких частот яких не є раціональним числом.
Перехідні – це все неперіодичні процеси, за винятком майже періодичних.
Випадкові - процеси, миттєві значення і параметри яких відомі у будь-який момент часу з ймовірністю меншою за одиницю.
Стаціонарний (слабо стаціонарний, стаціонарний в широкому сенсі) – процес, для якого перший і змішаний моменти, обчислені по ансамблю реалізацій не залежать від часу. Стаціонарний (строго стаціонарний, стаціонарний у вузькому
сенсі) – процес, для якого всі моменти і змішаний момент, обчислені по ансамблю реалізацій не залежать від часу.
Нестаціонарний - процес, для якого перший і змішаний моменти, обчислені по ансамблю реалізацій залежать від часу процес.
Ергодичний – стаціонарний процес, для якого моменти, обчислені по реалізаціях збігаються з моментами, обчисленими по ансамблю.
Неергодичний - стаціонарний процес, для якого моменти, обчислені по реалізаціях не збігаються з моментами, обчисленими по ансамблю.
Оскільки при моделюванні мають місце цифрові сигнали, необхідно забезпечити коректне дискретне подання випадкового процесу. Тут допомагає теорема Котельнікова, згідно якої для дискретизації аналогового сигналу з повним збереженням інформації в його цифровому еквіваленті максимальні частоти в аналоговому сигналі мають бути не менше ніж удвічі менше, ніж частота дискретизації, тобто fmax (1/2)fd.
Надалі розглянемо моделювання гармонічних сигналів. Найпростішим періодичним детермінованим сигналом є гармонійне коливання (струм, напруга, заряд, напруженість поля).
Суто гармонічне коливання називають монохроматичним коливанням. Спектр такого коливання складається з однієї спектральної лінії. У реальних сигналів, що мають початок і кінець, спектр неминуче ―розмивається‖. Тому суто монохроматичного коливання в природі не існує. Під гармонічним і монохроматичним сигналом умовно розуміється коливання, яке визначається функцією в інтервалі, хоча і скінченому, але достатньо значному.
Будь-який складний періодичний сигнал може бути представлений у вигляді суми гармонічних коливань з частотами, які складають гармонічну послідовність, тобто які кратні основній частоті 2 /T.
Окремі складові полігармонічного сигналу мають назву ―гармоніки‖. Коливання з частотою 1/Т називається першою гармонікою, з частотою 2/Т – другою гармонікою і т.д. Основною характеристикою полігармонічного сигналу є його спектральна функція, яка містить інформацію про амплітуди і фази окремих гармонік.
103.Розподіл Гауса. Щільність розподілу. Спектральна щільність
Нормальний закон розподілу (normal law of distribution) (який ще називається законом Гаусса) відіграє виключно важливу роль в теорії ймовірностей і займає серед інших законів розподілу особливий стан. Це закон, який найчастіше зустрічається на практиці. Головна особливість, яка виділяє нормальний закон серед інших законів, полягає в тому, що він є граничним законом, до якого наближаються інші закони розподілу.
Так, наприклад, велика кількість гарматних пострілів, здійснених в різних умовах, показує, що розсіювання снарядів на площині при пострілі з однієї гармати при встановленому прицілі підлягає нормальному закону.
―Універсальність‖ нормального закону пояснюється тим, що будь-яка випадкова величина, яка є сумою великої кількості окремих числових значень, кожне з яких підпорядковується різним законам розподілу і несуттєво впливає на суму, розподілена майже за нормальним законом.

Більшість випадкових величин, таких, наприклад, як похибки вимірів, похибки гарматних стрільб і т. д. можуть бути подані як суми великої кількості малих доданків - елементарних похибок, кожна з яких визначається дією окремої причини, яка не залежить від інших. Яким би законам розподілу не підпорядковувались окремі елементарні похибки, особливості цих розподілів в сумі великої кількості доданків нівелюються і сума підпорядковується закону, що близький до нормального. Підсумовані похибки в загальній сумі повинні грати відносно малу роль.
Випадкова величина ξ нормально розподілена або підпорядковується закону розподілу Гаусса, якщо її щільність розподілу має вигляд:
, де  - довільне дійсне число,
- довільне дійсне число,  > 0.
> 0.
Нижче буде доведено  Для безперервної випадкової величини дуже часто, можливо частіше ніж
Для безперервної випадкової величини дуже часто, можливо частіше ніж
сама функція розподілу, використовується похідна від функції розподілу – густина (щільність) розподілу випадкової величини X. Якщо функція розподілуF(x)є неперервною й такою, що диференціюється, тоді густина розподілу запишеться наступним чином:
Відповідно, якщо відома густина функції розподілу, тоді саму функцію розподілу отримують інтегруванням функції густини розподілу:
Функція густини розподілу (рис.__.б) також повністю визначає випадкову величину. Площа, яка обмежується віссю x, кривою функції та прямими x=x1таx = x2рівна ймовірності того, що випадкова величина прийме значення в інтерваліx1 x2:
Для побудови функції розподілу по відомій функції густини розподілу слід взяти інтеграл:
З цього можна отримати ще одна властивість функції густини функції розподілу:
так як попадання випадкової величини в інтервал - < X <є достовірною подією.
Однією з найважливіших характеристик детермінованого сигналу є спектр для періодичного сигналу і спектральна щільність для неперіодичного сигналу. Для їх знаходження використовується математичний апарат рядів Фур‘є і інтеграла Фур‘є.

Якщо сигнал U(t) детермінований неперіодичний, то його спектральну щільність легко знайти з використанням прямого перетворення Фур‘є.
Спробуємо застосувати пряме перетворення Фур‘є і для реалізації стаціонарного випадкового процесуХ(t).
На жаль, така процедура виявляється неможливою через дві причини.
1.Одержана спектральна щільність Sx(jω) тільки для однієї реалізації випадкового процесу. Інша реалізація того ж випадкового процесу матиме іншу спектральну щільність. Отже, перетворення Фур‘є у такому вигляді буде спектральною щільністю не самого випадкового процесу, а тільки однієї його реалізації.
2.Інша, важливіша причина, полягає в тому, що пряме перетворення Фур‘є можна застосовувати тільки до функцій, що задовольняють умові Дірехле
Ця умова ніколи не задовольняється для будь-якої реалізації стаціонарного в широкому сенсі випадкового процесу. Для застосування перетворення Фур‘є до реалізації стаціонарного процесу обмежимо його
тривалість інтервалом часу  .
.
Реалізація такого усіченого випадкового процесу задовольнятиме умові Дірехле і до неї можна застосувати перетворення Фур‘є.
104. Чисельні методи лінійної алгебри. Метод Гауса
Нехай дана система лінійних рівнянь виду (1), для якої потрібно знайти чисельний розв'язок:
Розглянемо розширену прямокутну матрицю, що складається з коєфіціентов системи (1) та її вільних членів:
Для даної матриці, згідно алгоритму методу Гаусса з вибором головного елемента, виберемо ненульовий, як правило, найбільший за модулем елемент, який не належить стовпцю вільних членів, тобто  . Нехай це буде
. Нехай це буде

елемент  (даний елемент також називають головним елементом). Далі, для кожного рядка матриці (2), крім рядка під номером
(даний елемент також називають головним елементом). Далі, для кожного рядка матриці (2), крім рядка під номером  , обчислюємо множники:
, обчислюємо множники:
Рядок під номером матриці , тобто |
рядок, який |
містить головний |
елемент, називається головним рядком. |
На наступному |
кроці виконуємо |
насутпні дії: до кожного неголовного рядка матриці |
додамо головний |
|
рядок помножений на відповідний для нього множник : |
|
|
В результаті отримаємо нову матрицю,  -та колонка якої складається з нульових елементів. Викреслюючи дану колонку і
-та колонка якої складається з нульових елементів. Викреслюючи дану колонку і  -й (головний) рядок, отримаємо матрицю
-й (головний) рядок, отримаємо матрицю  , яка складається з меншого на одиницю числа рядків і стовпців.
, яка складається з меншого на одиницю числа рядків і стовпців.
Над матрицею 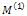 повторюємо тіж операції, після чого отримуємо деяку матрицю
повторюємо тіж операції, після чого отримуємо деяку матрицю  , і так далі продовжуємо даний процес. Таким чином ми отримуємо послідовність матриць
, і так далі продовжуємо даний процес. Таким чином ми отримуємо послідовність матриць  , остання з яких є матрицеюрядком, яка складається з двох елементів. Відмітимо, що даний рядок також вважається головним.
, остання з яких є матрицеюрядком, яка складається з двох елементів. Відмітимо, що даний рядок також вважається головним.
Для визначення невідомих  , об'єднуємо в систему, починаючи з останнього, який входить в матрицю
, об'єднуємо в систему, починаючи з останнього, який входить в матрицю  , всі головні рядки. Далі провівши відповідну перестановку рядків, отримуємо систему з трикутною матрицею, з допомогою якої, знаходимо невідомі системи (1). Метод Гаусса з вибором головного елементазастосовується для систем, детермінант яких відмінний від нуля:
, всі головні рядки. Далі провівши відповідну перестановку рядків, отримуємо систему з трикутною матрицею, з допомогою якої, знаходимо невідомі системи (1). Метод Гаусса з вибором головного елементазастосовується для систем, детермінант яких відмінний від нуля:
І на кінець зауважимо, що метод Гаусса, є окремим випадком методу головних елементів. Тобто в схемі методу Гаусса, за головний елемент завжди береться лівий верхній елемент відповідної матриці.
Розв'язок системи лінійних рівнянь методом Гаусcа з вибором головного елемента — приклад:
Використовуючи розглянутий алгоритм методу Гаусса з вибором головного елемента, знайти розв'язок системи лінійних рівнянь наступного виду:
Для зручності запишемо задану систему у вигляді прямокутної матриці (2):
Далі, слідуючи алгоритму методу, на першому етапі, серед елементів матриці  , вибираємо максимальний за модулем елемент, який не належить стовпцю вільних членів (головний елемент). В нашому випадку це буде елемент, який міститься в третьому рядку та четвертому стовпці (
, вибираємо максимальний за модулем елемент, який не належить стовпцю вільних членів (головний елемент). В нашому випадку це буде елемент, який міститься в третьому рядку та четвертому стовпці (  ). Після цього, для кожного рядка матриці, крім третього, скориставшись формулою (3), обчислюємо множники
). Після цього, для кожного рядка матриці, крім третього, скориставшись формулою (3), обчислюємо множники  :
:
